有一种游戏，有三根柱子，把一根柱子上的一摞从小到大排起来的圆盘挪到另一根柱子上，一次只能移动一个，

Posted 2023-03-30

有一种游戏，有三根柱子，把一根柱子上的一摞从小到大排起来的圆盘挪到另一根柱子上，一次只能移动一个，这个游戏叫什么

游戏叫做“汉诺塔”。

《汉诺塔》游戏玩的规则

1、把组成“金塔”的圆片按照下大上小依次放在中央的柱子上；

2、每次只能移动一个圆；

3、在移动过程中，大圆不能压在小圆上面；

4、每次移动的圆只能放在左中右的位子；5、将整座“金塔”移到另外任意一根柱子上即告胜利。

《汉诺塔》技巧
我们的目的是把这座“金塔”移到左边的柱子上，也就是要把这8个圆移到左边。我们就要想办法把压在最下面的圆8移到左边。要把圆8移到左边，就要把圆7移到右边。要把圆7移到右边，就要把圆6移到左边。要把圆6移到左边，就要把圆5移到右边。要把圆5移到右边，就要把圆4移到左边。要把圆4移到左边，就要把圆3移到右边。要把圆3移到右边，就要把圆2移到左边。要把圆2移到左边，就要把圆1移到右边。

从这里可以看出，圆1、3、5、7应移到右边，圆2、4、6、8应移到左边。由此也可以推导出圆7、5、3要去哪里，圆1就去那里，圆8、6、4去哪里，圆2就去那里。

这样我们就能在任何时候都能判断哪一个圆该走在什么位子上。

参考技术A

是《汉诺塔》。

游戏里有三根柱子，左边的柱子上从下往上按照大小顺序摞着N片圆盘。玩家需要做的是把圆盘从下面开始按从大顺序重新摆放在右边的柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

1、将塔A上的n-1个碟子借助塔C先移到塔B上。

2、把塔A上剩下的一个碟子移到塔C上。

3、将n-1个碟子从塔B借助塔A移到塔C上。

《汉诺塔》游戏中的道具：

一、柱子：在一个平板底座上间隔一定距离有三根完全一样的柱子1，2，3，柱子的长短决定于所移盘子的个数。

二、圆盘：在1号柱子上有n个大小不一的圆盘，圆盘的规格是从最底下一个开始，一个比一个小，可以有不同的颜色。

三、底座：长方体的木板，上有均匀的三个插孔。

参考技术B

有一种游戏，有三根柱子，把一根柱子上的一摞从小到大排起来的圆盘挪到另一根柱子上，一次只能移动一个，这个游戏叫做“汉诺塔”。

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。

把三根柱子按顺序排成“品”字型，把所有圆盘按从大到小的顺序放于柱子A上，根据圆盘数量来确定柱子排放的顺序：

n若为偶数的话，顺时针方向依次摆放为：ABC；而n若为奇数的话，就按顺时针方向依次摆放为：ACB。这样经过反复多次的测试，最后就可以按照规定完成汉诺塔的移动。

因此很简单的，结果就是按照移动规则向一个方向移动金片：

如3阶汉诺塔的移动：A→C，A→B，C→B，A→C，B→A，B→C，A→C。

汉诺塔的由来：

法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。

不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

参考技术C 汉诺塔，最高有9层本回答被提问者采纳 参考技术D 河内塔

汉诺塔的图解递归算法

原文链接：（转载请注明出处）https://dmego.me/2016/10/16/hanoi

一．起源：

　　汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

二．抽象为数学问题：

　　如下图所示，从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数

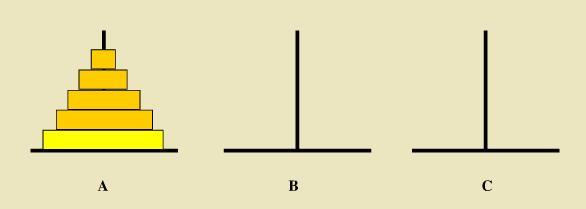
解：（1）n == 1

       　　　　　　第1次  1号盘  A---->C       sum = 1 次

       (2)  n == 2

       　　　　　　第1次  1号盘  A---->B

      　　　　　　 第2次  2号盘  A---->C

       　　　　　　第3次  1号盘  B---->C        sum = 3 次

　　（3）n == 3

　　　　　　　　第1次  1号盘  A---->C

　　　　　　　　第2次  2号盘  A---->B

　　　　　　　　第3次  1号盘  C---->B

　　　　　　　　第4次  3号盘  A---->C

　　　　　　　　第5次  1号盘  B---->A

　　　　　　　　第6次  2号盘  B---->C

　　　　　　　　第7次  1号盘  A---->C        sum = 7 次

 

不难发现规律：1个圆盘的次数 2的1次方减1

　　　　　　　2个圆盘的次数 2的2次方减1

                         3个圆盘的次数 2的3次方减1

                         。  。   。    。   。 

                         n个圆盘的次数 2的n次方减1

 故：移动次数为：2^n - 1

三．调用方法的栈机制:（特点：先进后出）

       从主线程开始调用方法（函数）进行不停的压栈和出栈操作，函数的调用就是将函数压如栈中，函数的结束就是函数出栈的过程，这样就保证了方法调用的顺序流，即当函数出现多层嵌套时，需要从外到内一层层把函数压入栈中，最后栈顶的函数先执行结束（最内层的函数先执行结束）后出栈，再倒数第二层的函数执行结束出栈，到最后，第一个进栈的函数调用结束后从栈中弹出回到主线程，并且结束。

四．算法分析（递归算法）：

       我们在利用计算机求汉诺塔问题时，必不可少的一步是对整个实现求解进行算法分析。到目前为止，求解汉诺塔问题最简单的算法还是同过递归来求，至于是什么是递归，递归实现的机制是什么，我们说的简单点就是自己是一个方法或者说是函数，但是在自己这个函数里有调用自己这个函数的语句，而这个调用怎么才能调用结束呢？，这里还必须有一个结束点，或者具体的说是在调用到某一次后函数能返回一个确定的值，接着倒数第二个就能返回一个确定的值，一直到第一次调用的这个函数能返回一个确定的值。

       实现这个算法可以简单分为三个步骤：

　　　　（1）     把n-1个盘子由A 移到 B；

　　　　（2）     把第n个盘子由 A移到 C；

　　　　（3）     把n-1个盘子由B 移到 C；

从这里入手，在加上上面数学问题解法的分析，我们不难发现，移到的步数必定为奇数步：

　　　　（1）中间的一步是把最大的一个盘子由A移到C上去；

　　　　（2）中间一步之上可以看成把A上n-1个盘子通过借助辅助塔（C塔）移到了B上，

　　　　（3）中间一步之下可以看成把B上n-1个盘子通过借助辅助塔（A塔）移到了C上；

五，java源代码：

package demo;
/**
 * 目的：实现汉诺塔问题求解
 * 作者：Dmego  时间：2016-10-15
 */
import java.util.Scanner;

public class TowersOfHanoi {
    static int m =0;//标记移动次数
    //实现移动的函数
    public static void move(int disks,char N,char M)
    {
        System.out.println("第" + (++m) +" 次移动 : " +" 把 "+ disks+" 号圆盘从 " + N +" ->移到->  " + M);
    }
    //递归实现汉诺塔的函数
    public static void hanoi(int n,char A,char B,char C)
    {
        if(n == 1)//圆盘只有一个时，只需将其从A塔移到C塔
            TowersOfHanoi.move(1, A, C);//将编b号为1的圆盘从A移到C
        else
        {//否则
            hanoi(n - 1, A, C, B);//递归，把A塔上编号1~n-1的圆盘移到B上，以C为辅助塔
            TowersOfHanoi.move(n, A, C);//把A塔上编号为n的圆盘移到C上
            hanoi(n - 1, B, A, C);//递归，把B塔上编号1~n-1的圆盘移到C上，以A为辅助塔
        }
    }
    public static void main(String[] args) {
        Scanner imput = new Scanner(System.in);
        char A = \'A\';
        char B = \'B\';
        char C = \'C\';
        System.out.println("******************************************************************************************");
        System.out.println("这是汉诺塔问题（把A塔上编号从小号到大号的圆盘从A塔通过B辅助塔移动到C塔上去");
        System.out.println("******************************************************************************************");
        System.out.print("请输入圆盘的个数：");
        int disks = imput.nextInt();
        TowersOfHanoi.hanoi(disks, A, B, C);
        System.out.println(">>移动了" + m + "次，把A上的圆盘都移动到了C上");
        imput.close();
    }

}

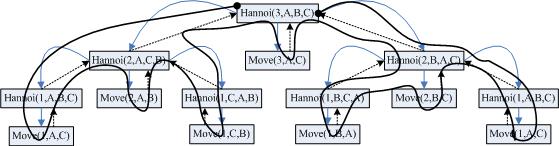
六．图解程序运行流程：

　　（1）函数hanoi(int n,char A,char B,char C)的功能是把编号为n的圆盘借助B从A移动到 C上。

　　（2）函数move(int n ,char N ,char M)的功能是把1编号为n的圆盘从N 移到M上

 

七．程序运行截图：