C. Kuroni and Impossible Calculation（抽屉原理）

Posted 2021-05-26 zjj0624

题意
给你一个数组$a$，让你求出

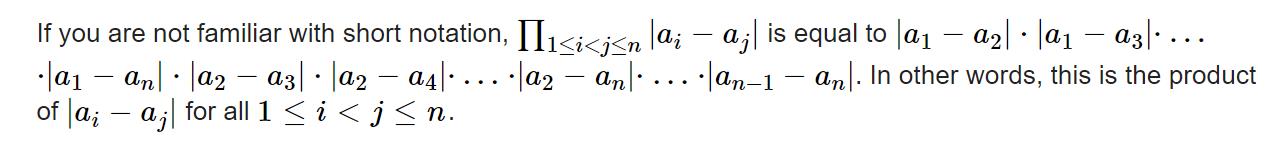
所有元素两个之间差的绝对值的乘积。
$100<=n<=200000,1<=m<=1000$
刚开始看到这个题，如果我们直接进行计算的话，时间复杂度是$o(n^2)$的，肯定是会超时的。
抽屉原理
如果有n个数（n>m）,必定有两个数是同模的。
也就是说必定有两个数对m取模值是相同的。
证明
对m取模以后，剩下的数是0，1，2，3，4，m-2，m-1，一共只有m种情况，如果有m+1个数，那必定有两个数是同模的。
我们再回过头看这个题，很容易发现，当（n>m）的时候，必定有两个数同模，也就是说这两个数相减以后肯定是m的倍数，如果是m的倍数，那最终结果对m取模肯定是0.
所以我们只需要考虑（n<=m）的情况，而m的范围很小，可以直接$n^2$求出结果。
代码

#include <bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define me memset
const int N = 1e6;
const int MOD = 1e9+7;
const int INF = 0x3f3f3f3f;
using namespace std;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
int n,m;
ll a[N];
int main()
{
    cin>>n>>m;
    for(int i=1 ; i<=n ; i++) cin>>a[i];
    if(n>m)
    {
        cout<<"0"<<endl;
        return 0;
    }
    else
    {
        ll ans=1;
        for(int i=1 ; i<=n ; i++)
        {
            for(int j=i+1 ; j<=n ; j++)
            {
                ans=((ans%m)*(abs(a[i]-a[j])%m))%m;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}