2018 ACM 四川省赛 G. Grisaia（超棒的杜教筛好题）

Posted 2021-05-25 繁凡さん

整理的算法模板合集： ACM模板

点我看算法全家桶系列！！！

实际上是一个全新的精炼模板整合计划

---

G. Grisaia（灰色的果实好耶《灰色的果实(The Fruit of Grisaia)》）

Weblink

https://www.oj.swust.edu.cn/problem/show/2810

Problem

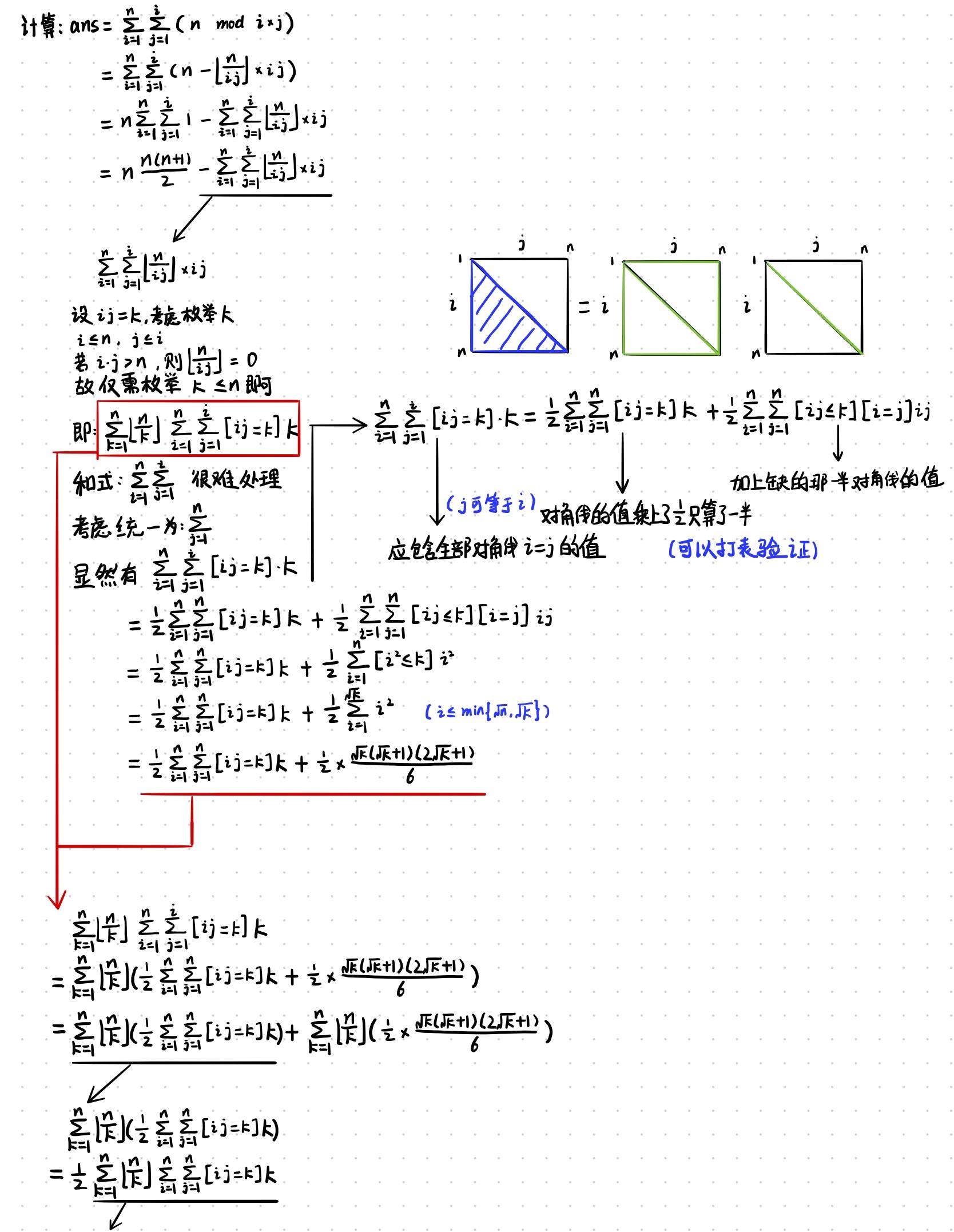
计算：

$$ans=\sum _{i=1}^n\sum _{j=1}^i(nmod(i\times j))$$

其中 $T\le 5,n\le 10^{11}$

Solution

使用模的展开式将上述和式展开后，显然套路枚举 $k=i\times j$，由于 $n\le 10^{11}$，杜教筛即可。

筛出：

$$\begin{gathered} f(x)=x\times d(x) \\ g(x)=x\times \mu (x) \end{gathered}$$

然后整除分块即可。

Hint

注意 $n\le 10^{11}$，中间多处会爆 long long，强转成 __int128 即可。

（因为这个wa了8发hhh，五颜六色的）

Code

#include <bits/stdc++.h>
   
using namespace std;
#define int long long
#define ll __int128
const int N = 31644346;
   
int n, m;
int mu[N];
int primes[N], cnt;
int d[N];
int num[N];
unordered_map<int, ll> sum_mui;
unordered_map<int, ll> sum_dk;
bool vis[N];
int sum[N];
   
inline ll read()
{
    register ll x = 0,f = 1;
    char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c-48,c = getchar();
    return x * f;
}
   
inline void print(ll x)
{
    if(x < 10)
    {
        putchar(x + 48);
        return;
    }
    print(x / 10), print(x % 10);
}
   
void init(int n)
{
    vis[0] = vis[1] = 1;
    mu[1] = d[1] = 1;
    for(int i = 2; i <= n; ++ i) {
        if(vis[i] == 0) {
            primes[ ++ cnt] = i;
            mu[i] = -1;
            d[i] = 2 * i;
            num[i] = 1;
        }
        for(int j = 1; j <= cnt && i * primes[j] <= n; ++ j) {
            vis[i * primes[j]] = 1;
            if(i % primes[j] == 0) {
                mu[i * primes[j]] = 0;
                num[i * primes[j]] = num[i] + 1;
                d[i * primes[j]] = (ll)d[i] / num[i * primes[j]] * (num[i * primes[j]] + 1) * primes[j];
                break;
            }
            mu[i * primes[j]] -= mu[i];
            num[i * primes[j]] = 1;
            d[i * primes[j]] = d[i] * d[primes[j]];
        }
    }
    for(int i = 1; i <= n; ++ i) {
        sum[i] = sum[i - 1] + mu[i] * i;
        d[i] = d[i - 1] + d[i];
    }
}
   
inline ll get_sum_mui(int x)
{
    if(x <= N - 7) return sum[x];
    if(sum_mui.find(x) != sum_mui.end()) return sum_mui[x];
       
    ll ans = 1;
    for(ll l = 2, r; l <= x; l = r + 1) {
        r = x / (x / l);
        ans -= (ll)(r - l + 1) * (l + r) / 2 * get_sum_mui(x / l);
    }   
    return sum_mui[x] = ans;
}
   
inline ll get_sum_dk(ll x)
{
    if(x <= N - 7) return d[x];
    if(sum_dk.find(x) != sum_dk.end()) return sum_dk[x];
    ll ans = x * (x + 1) / 2;
    for(ll l = 2, r; l <= x; l = r + 1) {
        r = x / (x / l);
        ans -= (ll)(get_sum_mui(r) - get_sum_mui(l - 1)) * get_sum_dk(x / l);
    }
    return sum_dk[x] = ans;
}
   
ll cal(ll x)
{
    ll limit = sqrt(x + 0.99);
    ll more = limit * (limit + 1) * (2 * limit + 1) / 6;
    return (get_sum_dk(x) + more) / 2;
}
   
void solve()
{
    ll ans = (ll)n * n * (n + 1) / 2;
    for(ll l = 1, r; l <= n; l = r + 1) {
        r = n / (n / l);
        //cout << "ok" << cal(r) - cal(l - 1) * (n / l) << endl;
        ans -= (ll)(cal(r) - cal(l - 1)) * (n / l);
    }
    print(ans);
    puts("");
}
   
signed main()
{
    int t;
    init(N - 7);
    t = read();
    while(t -- ) {
        n = read();
        solve();
    }
    return 0;
} 

Code2

大佬的AC代码：

（比我的代码快了几十倍…还没看懂）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef __int128 lll;
const int mod=1e9+7;
 
inline lll cal(lll l,lll r)
{
    return (l+r)*(r-l+1)/2;
}
 
inline lll solve(ll up)//solve \\sum_{i=1}^{n} up/i *i;
//显然只有i<=up时有贡献
{
//    num++;
//    if(num%10000==0) cout<<clock()<<endl;
    lll res=0;
    for(ll l=1,r;l<=up;l=r+1){
        r=up/(up/l);
        res=(res+up/l*cal(l,r));
    }
    return res;
}
 
inline void write(__int128 x)
{
    if(x<0)
    {
        putchar('-');
        x=-x;
    }
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
 
//lll help1[maxn];//solve f(n/1) f(n/2) f(n/3) f(n/\\sqrt(n))
//lll help2[maxn];//solve 1 2 3  \\sqrt{n}
const int maxn=21550000;
ll g[maxn];//n^(2/3)  g(n)=\\sum_{i|n} i
lll f[maxn];//sum_{i=1}^{n} [n/i]*i
ll ans[maxn/10];
bool valid[maxn];
int tot;
 
void get_prime(int n)
{
    memset(valid,true,sizeof(valid));
    tot=0;
    g[1]=1;
    for(int i=2;i<=n;++i){
        if(valid[i]){
            ans[++tot]=i;
            g[i]=i+1;
        }
        for(int j=1;j<=tot && ans[j]*i<=n;++j){
            valid[ans[j]*i]=false;
            if(i%ans[j]==0){
                //cout<<i<<" "<<ans[j]<<endl;
                //if(i*ans[j]==4)cout<<i<<" "<<g[i]<<" "<<ans[j]<<endl;
                int tp=1;
                int ti=i;
                while(ti%ans[j]==0){
                    tp*=ans[j];
                    ti/=ans[j];
                }
                tp*=ans[j];
                g[i*ans[j]]=g[i]*ans[j]+(g[i]/((tp-1)/(ans[j]-1)));
                break;
            }
            else g[i*ans[j]]=g[i]*g[ans[j]];
        }
    }
}
 
 
int main()
{
    get_prime(maxn);
//    for(int i=1;i<=30;++i) cout<<g[i]<<" ";
//    cout<<endl;
    f[0]=0;
    for(int i=1;i<maxn;++i) f[i]=f[i-1]+g[i];
    //cout<<clock()<<endl;
    //cout<<tot<<endl;
    //freopen("in.txt","r",stdin);
    int t;
    cin>>t;
    while(t--)
    {
        ll n;
        cin>>n;
        lll ans1=0;
        for(ll l=1,r;l<=n;l=r+1){
            r=n/(n/l);
            ll tp=n/l;
            if(tp<maxn) ans1+=f[tp]*cal(l,r);
            else ans1+=solve(tp)*cal(l,r);
        }
//        write(ans1);
//        cout<<endl;
        //cout<<clock()<<endl;
        lll ans2=0;//i=j
        for(ll i=1;i*i<=n;++i){
            ll tp=i*i;
            ans2+=n/tp*tp;
        }
//        write(ans2);
//        cout<<endl;
        ans1-=ans2;
        //assert(ans1%2==0);
        ans1/=2;
        ans1+=ans2;
//        write(ans1);
//        cout<<endl;
        ans1=((lll)n)*n*[ACM-ICPC 2018 沈阳网络赛] G. Spare Tire （思维+容斥)

 2017 ACM-ICPC 亚洲区（西安赛区）网络赛 G. Xor
 ACM-ICPC 2017 沈阳赛区现场赛 G. Infinite Fraction Path && HDU 6223
 费马小定理+快速幂取模ACM-ICPC 2018 焦作赛区网络预赛 G. Give Candies
 ACM-ICPC 2018 沈阳赛区网络预赛 G. Spare Tire
 ACM-ICPC 2018 徐州赛区网络预赛 G. Trace (set维护)