VRP问题基于matlab模拟退火算法求解带容量的VRP问题（多车型）

Posted 2021-05-25 Matlab咨询QQ1575304183

一、简介

模拟退火算法介绍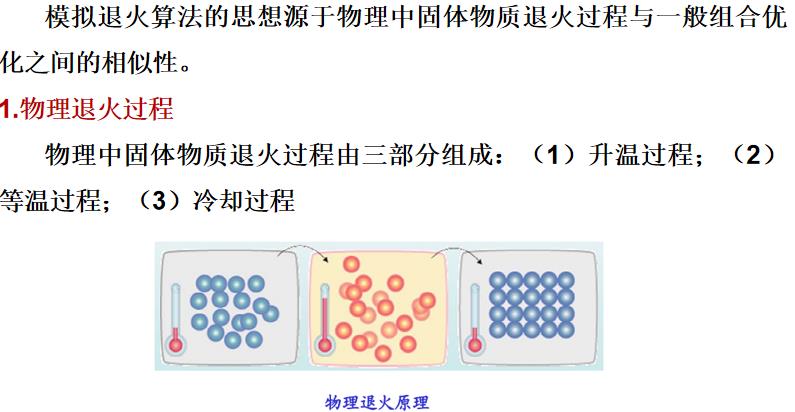




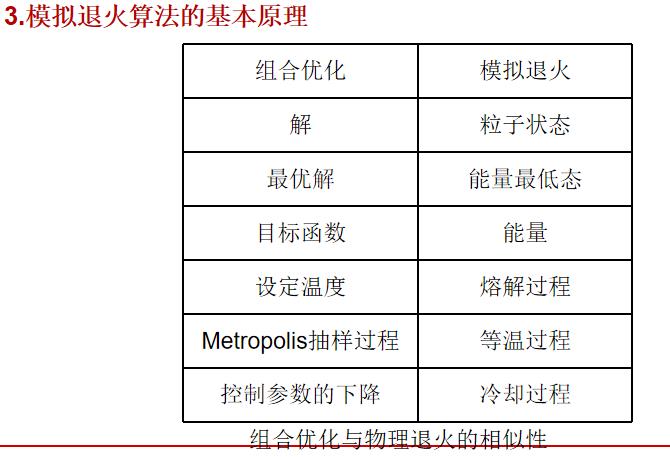
3 模拟退火算法的参数
模拟退火是一种优化算法，它本身是不能独立存在的，需要有一个应用场合，其中温度就是模拟退火需要优化的参数，如果它应用到了聚类分析中，那么就是说聚类分析中有某个或者某几个参数需要优化，而这个参数，或者参数集就是温度所代表的。它可以是某项指标，某项关联度，某个距离等等。

二、源代码

%%
%

clc;
clear;
close all;

%% Problem Definition

model=SelectModel();        % Select Model of the Problem

model.eta=0.1;

CostFunction=@(q) MyCost(q,model);       % Cost Function

%% SA Parameters

MaxIt=500;     % Maximum Number of Iterations

MaxIt2=80;      % Maximum Number of Inner Iterations

T0=100;         % Initial Temperature

alpha=0.98;     % Temperature Damping Rate


%% Initialization

% Create Initial Solution
x.Position=CreateRandomSolution(model);
[x.Cost, x.Sol]=CostFunction(x.Position);

% Update Best Solution Ever Found
BestSol=x;

% Array to Hold Best Cost Values
BestCost=zeros(MaxIt,1);

% Set Initial Temperature
T=T0;


%% SA Main Loop

for it=1:MaxIt
    for it2=1:MaxIt2
        
        % Create Neighbor
        xnew.Position=CreateNeighbor(x.Position);
        [xnew.Cost, xnew.Sol]=CostFunction(xnew.Position);
        
        if xnew.Cost<=x.Cost
            % xnew is better, so it is accepted
            x=xnew;
            
        else
            % xnew is not better, so it is accepted conditionally
            delta=xnew.Cost-x.Cost;
            p=exp(-delta/T);
            
            if rand<=p
                x=xnew;
            end
            
        end
        
        % Update Best Solution
        if x.Cost<=BestSol.Cost
            BestSol=x;
        end
        
    end
    
    % Store Best Cost
    BestCost(it)=BestSol.Cost;

    
    % Display Iteration Information
    if BestSol.Sol.IsFeasible
        FLAG=' *';
    else
        FLAG='';
    end
    disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it)) FLAG]);
    
    % Reduce Temperature
    T=alpha*T;
    
    % Plot Solution
    figure(1);
    PlotSolution(BestSol.Sol,model);
    pause(0.01);
    
end
%
 

function model=CreateRandomModel(I,J)

    rmin=10;
    rmax=25;
    r=randi([rmin rmax],1,I);
    
    TotalDemand=sum(r);
    cmean=TotalDemand/J;
    cmin=round(cmean);
    cmax=round(1.25*cmean);
    c=randi([cmin cmax],1,J);
    
    xmin=0;
    xmax=200;
    
    ymin=0;
    ymax=100;
    
    x=randi([xmin xmax],1,I);
    y=randi([ymin ymax],1,I);
    
    alpha_x=0.1;
    xm=(xmin+xmax)/2;
    dx=xmax-xmin;
    x0min=round(xm-alpha_x*dx);
    x0max=round(xm+alpha_x*dx);
    
    alpha_y=0.1;
    ym=(ymin+ymax)/2;
    dy=ymax-ymin;
    y0min=round(ym-alpha_y*dy);
    y0max=round(ym+alpha_y*dy);
    
    x0=randi([x0min x0max]);
    y0=randi([y0min y0max]);
    
    d=zeros(I,I);
    d0=zeros(1,I);
    for i=1:I
        for i2=i+1:I
            d(i,i2)=sqrt((x(i)-x(i2))^2+(y(i)-y(i2))^2);
            d(i2,i)=d(i,i2);
        end
        
        d0(i)=sqrt((x(i)-x0)^2+(y(i)-y0)^2);
    end
    
    eta=0.5;
    
    model.I=I;
    model.J=J;
    model.r=r;
    model.c=c;
    model.xmin=xmin;
    model.xmax=xmax;
    model.ymin=ymin;
    model.ymax=ymax;
    model.x=x;
    model.y=y;
    model.x0=x0;
    model.y0=y0;
    model.d=d;
    model.d0=d0;
    model.eta=eta;

end
%


function qnew=CreateNeighbor(q)

    m=randi([1 3]);
    
    switch m
        case 1
            % Do Swap
            qnew=Swap(q);
            
        case 2
            % Do Reversion
            qnew=Reversion(q);
            
        case 3
            % Do Insertion
            qnew=Insertion(q);
    end

end

function qnew=Swap(q)

    n=numel(q);
    
    i=randsample(n,2);
    i1=i(1);
    i2=i(2);
    
    qnew=q;
    qnew([i1 i2])=q([i2 i1]);
    
end

function qnew=Reversion(q)

    n=numel(q);
    
    i=randsample(n,2);
    i1=min(i(1),i(2));
    i2=max(i(1),i(2));
    
    qnew=q;
    qnew(i1:i2)=q(i2:-1:i1);

end

function qnew=Insertion(q)

    n=numel(q);
    
    i=randsample(n,2);
    i1=i(1);
    i2=i(2);
    
    if i1<i2
        qnew=[q(1:i1-1) q(i1+1:i2) q(i1) q(i2+1:end)];
    else
        qnew=[q(1:i2) q(i1) q(i2+1:i1-1) q(i1+1:end)];
    end

end

三、运行结果

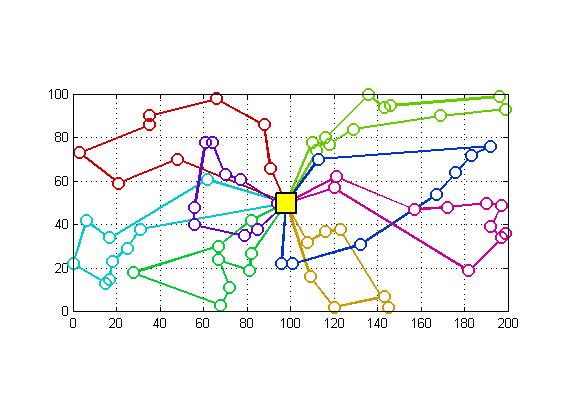
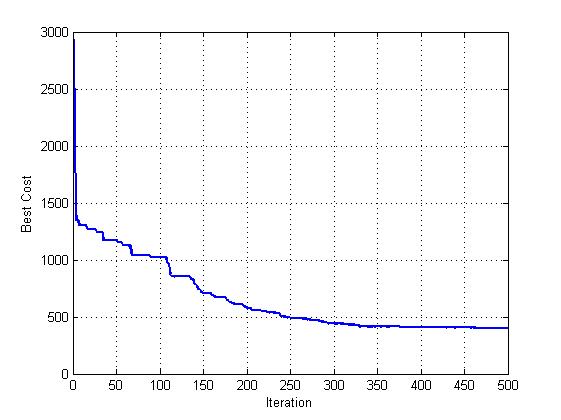
四、备注

版本：2014a