数据结构C语言篇《三》栈和队列概念,模拟函数实现,以及相关OJ面试题
Posted 程序猿是小贺
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构C语言篇《三》栈和队列概念,模拟函数实现,以及相关OJ面试题相关的知识,希望对你有一定的参考价值。
栈和队列
1. 栈

栈,存储货物或供旅客住宿的地方,可引申为仓库、中转站,所以引入到计算机领域里,就是指数据暂时存储的地方,所以才有进栈、出栈的说法。可以类比相当于吃饭,吃进去吐出来就是栈(忍着胃部强烈不适码了这句)
1.1栈的概念
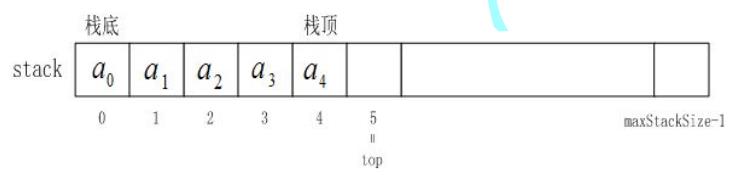
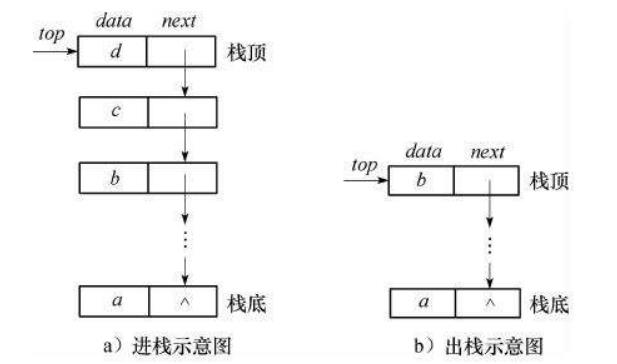
栈(stack)又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
栈的特性:后进先出
注意:栈不能进行遍历操作
1.2栈的实现方法
栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现更优一些。因为数组在尾上插入数据的
代价比较小。
1.3栈的模拟实现----动态内存
Stack.h
#pragma once
typedef int DataType;
typedef struct Stcak
{
DataType *arr;
int capacity; //容量大小
int size; //有效元素个数---栈顶
}Stack;
//栈的初始化
void StackInit(Stack *ps);
//入栈
void StackPush(Stack *ps, DataType data);
//出栈
void StackPop(Stack *ps);
//获取栈顶元素
DataType StackTop(Stack *ps);
//获取栈的大小
int StackSize(Stack *ps);
//判断栈内是否有元素
int StackEmpty(Stack *ps);
//销毁栈
void StackDestroy(Stack *ps);
void TestStack();
Stack.c
#include"Stack.h"
#include<stdio.h>
#include<assert.h>
#include<malloc.h>
//栈的初始化
void StackInit(Stack *ps)
{
assert(ps);
ps->arr = (DataType *)malloc(sizeof(DataType)* 3);
if (NULL == ps->arr) //检测空间是否申请成功
{
assert(0);
return;
}
ps->capacity = 3;;
ps->size = 0;
}
//检查容量
void CheckCapacity(Stack *ps)
{
if (ps->size == ps->capacity)
{
ps->arr = (DataType*)realloc(ps->arr, sizeof(DataType)*ps->capacity * 2);
if (NULL == ps->arr) //检测空间是否申请成功
{
assert(0);
return;
}
ps->capacity *= 2;
}
}
//入栈
void StackPush(Stack *ps, DataType data)
{
assert(ps);
CheckCapacity(ps); //扩容
ps->arr[ps->size++] = data;
}
//出栈
void StackPop(Stack *ps)
{
assert(ps);
if (StackEmpty(ps)) //检测栈此时是否为空
return;
ps->size--;
}
//获取栈顶元素
DataType StackTop(Stack *ps)
{
assert(ps && !StackEmpty(ps));
//此处不能使用if条件判断,因为if条件判断的为合法情况
//若是栈为空此时栈没有元素,要获取栈顶元素 则为非法情况
//可以用assert进行判断
//if (StackEmpty(ps))
// return;
return ps->arr[ps->size - 1];
}
//获取栈的大小
int StackSize(Stack *ps)
{
assert(ps);
return ps->size;
}
//判断栈内是否有元素
int StackEmpty(Stack *ps)
{
assert(ps);
return 0 == ps->size;
}
//销毁栈
void StackDestroy(Stack *ps)
{
assert(ps);
if (ps->arr)
{
free(ps->arr);
ps->arr = NULL;
ps->capacity = 0;
ps->size = 0;
}
}
void TestStack()
{
Stack con;
StackInit(&con);
StackPush(&con, 1);
StackPush(&con, 2);
StackPush(&con, 3);
StackPush(&con, 4);
StackPush(&con, 5);
StackPush(&con, 6);
printf("size = %d\\n", StackSize(&con));
printf("top = %d\\n", StackTop(&con));
StackPop(&con);
StackPop(&con);
StackPop(&con);
printf("size = %d\\n", StackSize(&con));
printf("top = %d\\n", StackTop(&con));
StackDestroy(&con);
}
test.c
#define _CRT_SECURE_NO_WARNINGS
#include"Stack.h"
int main()
{
TestStack();
return 0;
}
1.4关于栈的OJ题
typedef char DataType;
typedef struct Stcak
{
DataType *arr;
int capacity; //容量大小
int size; //有效元素个数---栈顶
}Stack;
//栈的初始化
void StackInit(Stack *ps)
{
assert(ps);
ps->arr = (DataType *)malloc(sizeof(DataType)* 3);
if (NULL == ps->arr) //检测空间是否申请成功
{
assert(0);
return;
}
ps->capacity = 3;;
ps->size = 0;
}
//检查容量
void CheckCapacity(Stack *ps)
{
if (ps->size == ps->capacity)
{
ps->arr = (DataType*)realloc(ps->arr, sizeof(DataType)*ps->capacity * 2);
if (NULL == ps->arr) //检测空间是否申请成功
{
assert(0);
return;
}
ps->capacity *= 2;
}
}
//入栈
void StackPush(Stack *ps, DataType data)
{
assert(ps);
CheckCapacity(ps); //扩容
ps->arr[ps->size++] = data;
}
//出栈
void StackPop(Stack *ps)
{
assert(ps);
if (StackEmpty(ps)) //检测栈此时是否为空
return;
ps->size--;
}
//获取栈顶元素
DataType StackTop(Stack *ps)
{
//assert(ps);
assert(ps && !StackEmpty(ps));
//此处不能使用if条件判断,因为if条件判断的为合法情况
//若是栈为空此时栈没有元素,要获取栈顶元素 则为非法情况
//可以用assert进行判断
return ps->arr[ps->size - 1];
}
//获取栈的大小
int StackSize(Stack *ps)
{
assert(ps);
return ps->size;
}
//判断栈内是否有元素
int StackEmpty(Stack *ps)
{
assert(ps);
return 0 == ps->size;
}
//销毁栈
void StackDestroy(Stack *ps)
{
assert(ps);
if (ps->arr)
{
free(ps->arr);
ps->arr = NULL;
ps->capacity = 0;
ps->size = 0;
}
}
bool isValid(char * s)
{
bool flag=false;
Stack ms;
StackInit(&ms);
int n=strlen(s);
if(n%2==0)
{
for(int i=0;i<n;i++)//遍历
{
//如果检测该括号为左括号,则入栈
if(s[i]=='('||s[i]=='['||s[i]=='{')
{
StackPush(&ms,s[i]);
}
else
{
//当前取的括号为右括号且此时栈刚好为空
if(StackEmpty(&ms))
{
StackDestroy(&ms);
return false;
}
char top=StackTop(&ms);
if((top=='('&&s[i]==')')||
(top=='['&&s[i]==']')||
(top=='{'&&s[i]=='}'))
{
StackPop(&ms);
}
else
{
break;
}
}
}
if(StackEmpty(&ms))
{
flag=true;
}
StackDestroy(&ms);
return flag;
}
else
{
StackDestroy(&ms);
return false;
}
}
1.5逆波兰表达式
1.5.1概念
逆波兰表达式又叫做后缀表达式,逆波兰表示法是波兰逻辑学家J・卢卡西维兹(J・ Lukasiewicz)于1929年首先提出的一种表达式的表示方法 [1] 。后来,人们就把用这种表示法写出的表达式称作“逆波兰表达式”。逆波兰表达式把运算量写在前面,把算符写在后面。
1.5.2栈实现逆波兰表达式
它的优势在于只用两种简单操作,入栈和出栈就可以搞定任何普通表达式的运算。其运算方式如下:
如果当前字符为变量或者为数字,则压栈,如果是运算符,则将栈顶两个元素弹出作相应运算,结果再入栈,最后当表达式扫描完后,栈里的就是结果。
2.队列
相当于吃进去拉出来。
2.1队列的概念
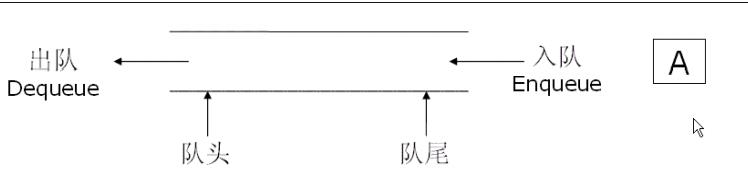
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,进行插入操作的一端称为队尾 出队列,进行删除操作的一端称为队头。
队列的特性:先进先出。
2.2队列的实现方法
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,效率会比较低。
2.3队列的模拟实现----链式
Queue.h
#pragma once
typedef int QDataType;
typedef struct QListNode
{
struct QListNode* next;
QDataType data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* front;
QNode* rear;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);
Queue.c
#include"Queue.h"
#include<assert.h>
#include<stdio.h>
#include<malloc.h>
QNode* BuyQueueNode(QDataType data)
{
QNode* node = (QNode *)malloc(sizeof(QNode));
if (NULL == node)
{
assert(0);
return NULL;
}
node->data = data;
node->next = NULL;
return node;
}
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);
q->front = q->rear = BuyQueueNode(0);
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
q->rear->next = BuyQueueNode(data);
q->rear = q->rear->next;
}
// 队头出队列
void QueuePop(Queue* q)
{
QNode *delNode = NULL;
if (QueueEmpty(q))
return;
delNode = q->front->next;
q->front->next = delNode->next;
//如果队列中此时只有一个元素,将该元素删除后还需将rear放在front的位置
if (delNode->next == NULL)
q->rear = q->front;
free(delNode);
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(!QueueEmpty(q));
return q->front->next->data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(!QueueEmpty(q));
return q->rear->data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
int count = 0;
QNode* cur = q->front->next;
while (cur)
{
cur = cur->next;
count++;
}
return count;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
assert(q);
return q->front->next == NULL;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
q->front = cur->next;
free(cur);
cur = q->front;
}
q->front = q->rear = NULL;
}
//测试
void TestQueue()
{
Queue q;
QueueInit(&q);
QueuePush(&q, 1);
QueuePush(&q, 2);
QueuePush(&q, 3);
QueuePush(&q, 4);
QueuePush(&q, 5);
QueuePush(&q, 6);
printf("size = %d\\n", QueueSize(&q));
printf("front = %d\\n", QueueFront(&q));
printf("rear = %d\\n", QueueBack(&q));
QueuePop(&q);
QueuePop(&q);
QueuePop(c 语言数据结构栈和队列的相关操作