六大查找算法(Python 语言实现)
Posted Amo Xiang
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了六大查找算法(Python 语言实现)相关的知识,希望对你有一定的参考价值。
目录
一、顺序查找算法
顺序查找又称为线性查找,是最简单的查找算法。这种算法就是按照数据的顺序一项一项逐个查找,所以不管数据顺序如何,都得从头到尾地遍历一次。顺序查找的优点就是数据在查找前,不需要对其进行任何处理(包括排序)。缺点是查找速度慢,如果数据列的第一个数据就是想要查找的数据,则该算法查找速度为最快,只需查找一次即可;如果查找的数据是数据列的最后一个(第几个),则该算法查找速度为最慢,需要查找 n 次,甚至还会出现未找到数据的情况。
例如,有这样一组数据:10、27、13、14、19、85、70、29、69、27。如果想要查找数据 19,需要进行 5 次查找;如果想要查找数据 27,需要进行 10 次查找;如果想要查找数据 10,只需要进行 1 次查找。
从这个例子中可以看出,当查找的数据较多时,用顺序查找就不太合适,所以说顺序查找只能应用于查找数据较少的数据列。这个过程好比我们在抽屉里找笔,如下图所示。通常情况下我们会从上层的抽屉开始,一层一层地查找,直到找到笔为止,这个例子就是生活中典型的顺序查找算法。

例如,随机从 1~100 之间生成 50 个整数,并将随机生成的这 50 个数显示出来,然后用顺序查找算法查找16、45、97这几个数据的位置。具体代码如下:
import random # 导入随机数模块
num = 0 # 定义变量num
# 使用列表推导式生成包含50个元素的列表
data = [random.randint(1, 100) for i in range(50)]
print("随机产生的数据内容是:")
for i in range(10): # 遍历行
for j in range(5): # 遍历列
# 按格式输出随机生成内容
print('%2d[%3d] ' % (i * 5 + j + 1, data[i * 5 + j]), end='')
print('')
while num != -1: # 循环输入
find = 0 # 比较次数
num = int(input("请输入想要查找的数据,输入-1退出程序:")) # 数据输入
for i in range(50): # 循环遍历50个随机数
if data[i] == num: # 判断输入数据和data数据是否相等
print("在", i + 1, "个位置找到数据", data[i]) # 输出找到的位置和数据内容
find += 1 # 比较次数加1
if find == 0 and num != -1: # 判断比较次数是否为0且输入数据是否为-1
print("没有找到", num, "此数据") # 提示没有找到数据
程序运行结果如下图所示:
二、折半查找算法
折半查找算法又称为二分查找算法,折半查找算法是将数据分割成两等份,首先用键值(要查找的数据)与中间值进行比较。如果键值小于中间值,可确定要查找的键值在前半段;如果键值大于中间值,可确定要查找的键值在后半段。然后对前半段(后半段)进行分割,将其分成两等份,再对比键值。如此循环比较、分割,直到找到数据或者确定数据不存在为止。折半查找的缺点是只适用于已经初步排序好的数列;优点是查找速度快。
生活中也有类似于折半查找的例子,例如,猜数字游戏。在游戏开始之前,首先会给出一定的数字范围(例如0~100),并在这个范围内选择一个数字作为需要被猜的数字。然后让用户去猜,并根据用户猜的数字给出提示(如猜大了或猜小了)。用户通常的做法就是先在大范围内随意说一个数字,然后提示猜大了/猜小了,这样就缩小了猜数字的范围,慢慢地就猜到了正确的数字,如下图所示。这种做法与折半查找法类似,都是通过不断缩小数字范围来确定数字,如果每次猜的范围值都是区间的中间值,就是折半查找算法了。
例如,已经有 排序好 的数列:12、45、56、66、77、80、97、101、120,要查找的数据是 101,用折半查找步骤如下:
步骤1:将数据列出来并找到中间值 77,将 101 与 77 进行比较,如下图所示。
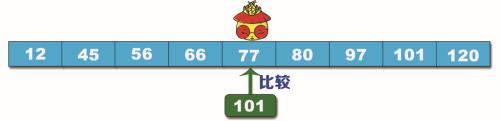
步骤2:将 101 与 77 进行比较,结果是 101 大于 77,说明要查找的数据在数列的右半段。此时不考虑左半段的数据,对在右半段的数据再进行分割,找中间值。这次中间值的位置在 97 和 101 之间,取 97,将 101 与 97 进行比较,如下图所示。
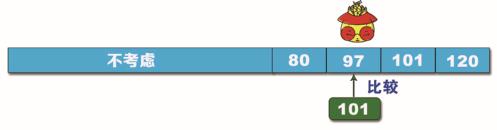
步骤3:将 101 与 97 进行比较,结果是 101 大于 97,说明要查找的数据在右半段数列中,此时不考虑左半段的数据,再对剩下的数列分割,找中间值,这次中间值位置是 101,将 101 与 101 进行比较,如下图所示。

步骤4:将 101 与 101 进行比较,所得结果相等,查找完成。说明:如果多次分割之后没有找到相等的值,表示这个键值没有在这个数列中。
从折半法查找的步骤来看,明显比顺序查找法的次数少,这就是折半查找法的优点:查找速度快。
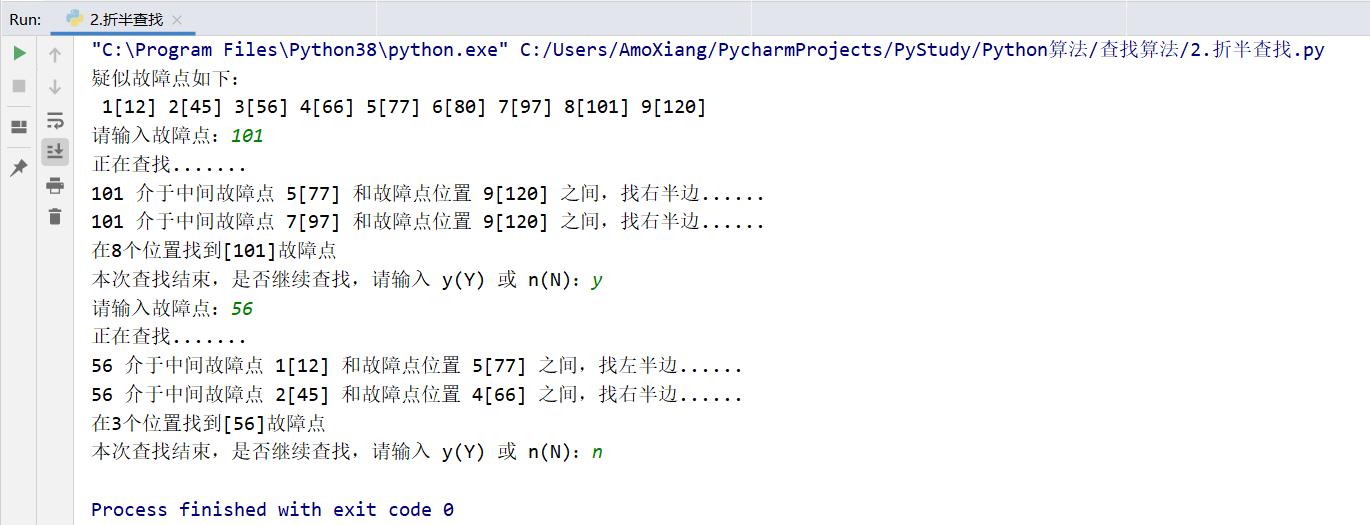
有一条的150米线路,在这条线路上存在故障。第一天维修工已经大致锁定了几个疑似故障点,疑似故障点分别在线路的12、45、56、66、77、80、97、101、120米处。第二天维修工要在这9个疑似故障点中确定一个真正的故障点(假设真正的故障点是101米处)。维修工为了快速查找此故障点,就在每段数据的中间位置开始排查。
例如,第一次选择在77米处的疑似故障点接通电路,发现接通,他判断此故障在77米之后的位置;第二次取97米处的疑似故障点,发现也接通了,说明在97米之后的位置;第三次取101米处的位置,再次接通线路,发现未接通,说明此处是真正的故障点。此次查找经历了3次,将真正故障点找到。具体代码如下:
def search(data, num):
"""
定义查找函数:该函数使用的是折半查找算法
:param data: 原数列data
:param num: 键值num
:return:
"""
low = 0 # 定义变量用来表示低位
high = len(data) - 1 # 定义变量用来表示高位
print("正在查找.......") # 提示
while low <= high and num != -1:
mid = int((low + high) / 2) # 取中间位置
if num < data[mid]: # 判断数据是否小于中间值
# 输出位置在数列中的左半边
print(f"{num} 介于中间故障点 {low + 1}[{data[low]}] 和故障点位置 {mid + 1}[{data[mid]}] 之间,找左半边......")
high = mid - 1 # 最高位变成了中间位置减1
elif num > data[mid]: # 判断数据是否大于中间值
# 输出位置在数列中的右半边
print(f"{num} 介于中间故障点 {mid + 1}[{data[mid]}] 和故障点位置 {high + 1}[{data[high]}] 之间,找右半边......")
low = mid + 1 # 最低位变成了中间位置加1
else: # 判断数据是否等于中间值
return mid # 返回中间位置
return -1 # 自定义函数到此结束
inp_num = 0 # 定义变量,用来输入键值
num_list = [12, 45, 56, 66, 77, 80, 97, 101, 120] # 定义数列
print("疑似故障点如下:")
for index, ele in enumerate(num_list):
print(f" {index + 1}[{ele}]", end="") # 输出数列
print("")
flag = True # 开关,用来管控是否多次查找
while flag: # 循环查找
inp_num = int(input("请输入故障点:").strip()) # 输入查找键值
if inp_num == -1: # 判断键值是否是-1
break # 若为-1,跳出循环 即结束程序
result = search(num_list, inp_num) # 调用自定义的查找函数——search()函数
if result == -1: # 判断查找结果是否是-1
print(f"没有找到[{inp_num}]故障点") # 若为-1,提示没有找到值
else:
# 若不为-1,提示查找位置
print(f"在{result + 1}个位置找到[{num_list[result]}]故障点")
char = input("本次查找结束,是否继续查找,请输入 y(Y) 或 n(N):").strip()
if char.upper() == "N":
flag = False
程序执行结果如下图所示:
三、插补查找算法
插补查找算法又称为插值查找,它是折半查找算法的改进版。插补查找是按照数据的分布,利用公式预测键值所在的位置,快速缩小键值所在序列的范围,慢慢逼近,直到查找到数据为止。根据描述来看,插值查找类似于平常查英文字典的方法。例如,在查一个以字母 D 开头的英文单词时,决不会用折半查找法。根据英文词典的查找顺序可知,D 开头的单词应该在字典较前的部分,因此可以从字典前部的某处开始查找。键值的索引计算,公式如下:
middle=left+(target-data[left])/(data[right]-data[left])*(right-left)
参数说明:
- middle:所求的边界索引。
- left:最左侧数据的索引。
- target:键值(目标数据)。
- data[left]:最左侧数据值。
- data[right]:最右侧数据值。
- right:最右侧数据的索引。
例如,已经有排序好的数列:34、53、57、68、72、81、89、93、99。要查找的数据是 53,使用插补查找法步骤如下:
步骤1:将数据列出来并利用公式找到边界值,计算过程如下:
将各项数据带入公式:
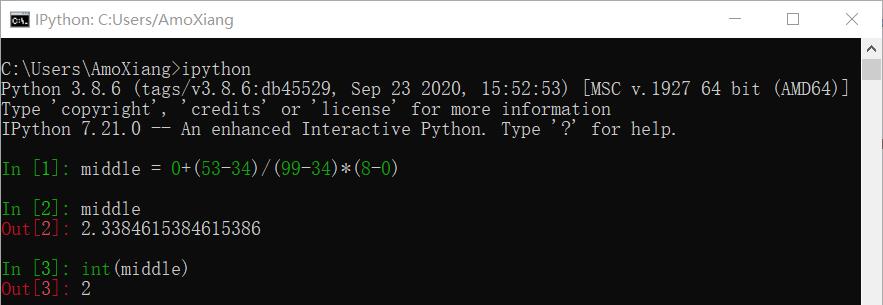
将数据取整,因此所求索引是 2,对应的数据是 57,将查找目标数据 53 与 57 进行比较,如下图所示。
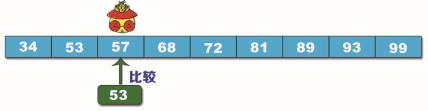
步骤2:将 53 与 57 进行比较,结果是 53 小于 57,所以查找 57 的左半边数据,不用考虑右半边的数据,索引范围缩小到 0 和 2 之间,公式带入:
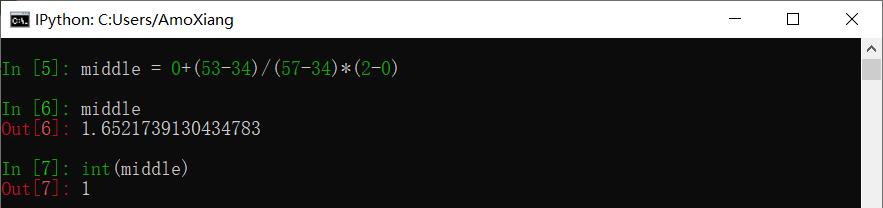
取整之后索引是 1,对应的数据是 53,将查找目标数据 53 与 53 进行比较,如下图所示:

步骤3:将 53 与 53 进行比较,所得结果相等,查找完成。说明:如果多次分割之后没有找到相等的值,表示这个键值没有在这个数列中。
通过上述的步骤1就能看出,插补查找算法比折半查找算法的取值范围更小,因此它的速度要比折半法查找快,这就是插补查找算法的优点。
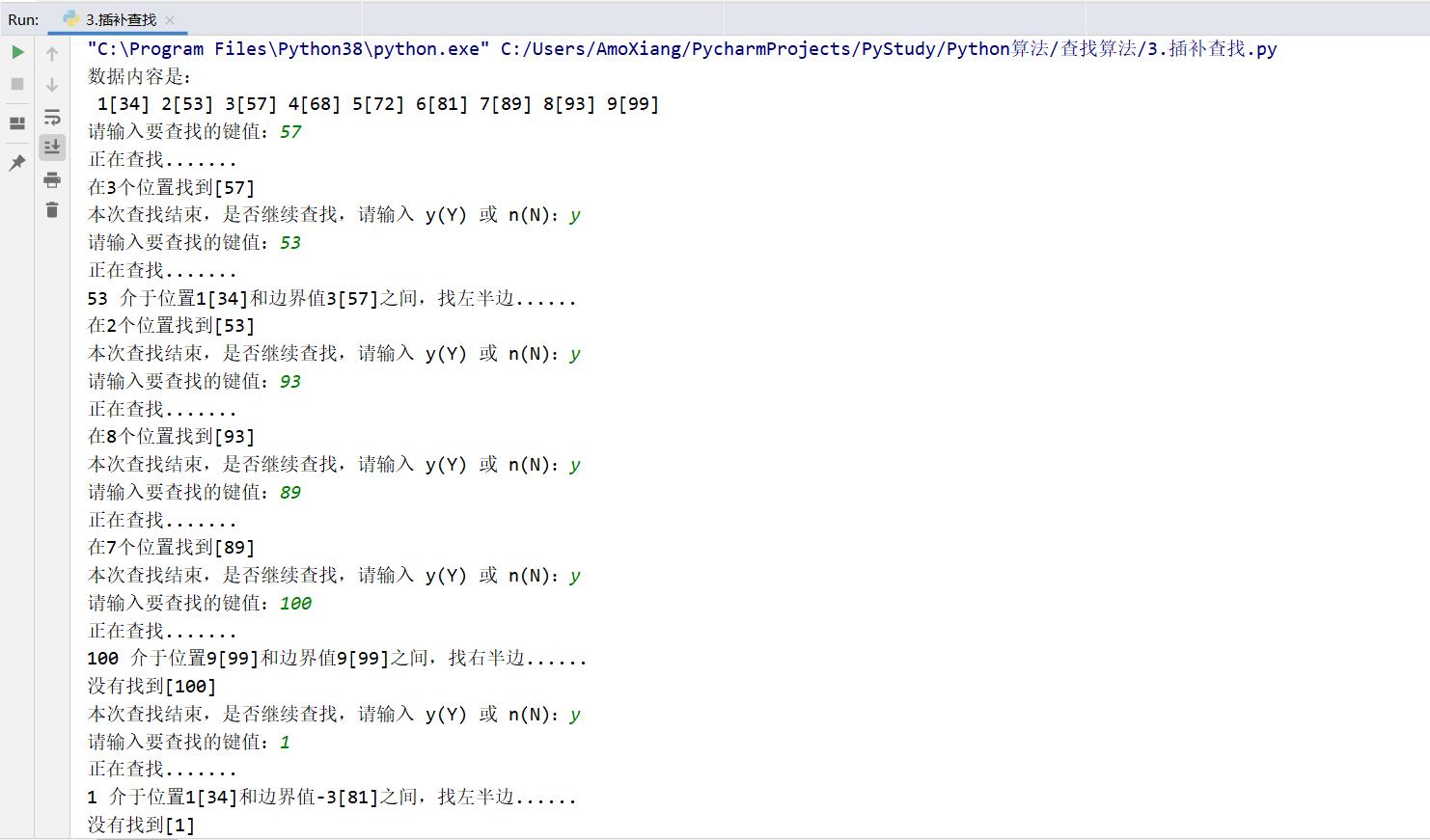
用户可以随意输入一组数据,例如本实例输入一组数据:34、53、57、68、72、81、89、93、99。在这组数据中用插补查找法分别查找数据 57、53、93、89、100,且显示每次查找的过程。用 Python 代码实现此过程,具体代码如下:
def insert_search(data, num):
"""
自定义查找函数:该函数使用的是插补查找算法
:param data: 原数列data
:param num: 键值num
:return:
"""
# 计算
left_index = 0 # 最左侧数据的索引
right_index = len(data) - 1 # 最右侧数据的索引
print("正在查找.......") # 提示
while left_index <= right_index:
# 使用公式计算出索引值
middle = left_index + (num - data[left_index]) / (data[right_index] - data[left_index]) * (
right_index - left_index)
# 取整
middle = int(middle)
# print(middle)
if num == data[middle]:
return middle # 如果键值等于边界值,返回边界位置
elif num < data[middle]:
# 输出位置在数列中的左半边
print(f"{num} 介于位置{left_index + 1}[{data[left_index]}]和边界值{middle + 1}[{data[middle]}]之间,找左半边......")
right_index = middle - 1 # 如果键值小于边界值,最右边数据索引等于边界位置减1
else:
# 输出位置在数列中的左半边
print(f"{num} 介于位置{middle + 1}[{data[middle]}]和边界值{right_index + 1}[{data[right_index]}]之间,找右半边......")
left_index = middle + 1 # 如果键值大于边界值,最左边数据索引等于边界位置加1
return -1 # 自定义函数到此结束
inp_num = 0 # 定义变量,用来输入键值
num_list = [34, 53, 57, 68, 72, 81, 89, 93, 99] # 定义数列
print("数据内容是:")
for index, ele in enumerate(num_list):
print(f" {index + 1}[{ele}]", end="") # 输出数列
print("")
flag = True # 开关,用来管控是否多次查找
while flag: # 循环查找
inp_num = int(input("请输入要查找的键值:").strip()) # 输入查找键值
result = insert_search(num_list, inp_num) # 调用自定义的查找函数——insert_search()函数
if result == -1: # 判断查找结果是否是-1
print(f"没有找到[{inp_num}]") # 若为-1,提示没有找到值
else:
# 若不为-1,提示查找位置
print(f"在{result + 1}个位置找到[{inp_num}]")
char = input("本次查找结束,是否继续查找,请输入 y(Y) 或 n(N):").strip()
if char.upper() == "N":
flag = False
程序执行结果如下图所示:
四、哈希查找算法
哈希查找算法是使用哈希函数来计算一个键值所对应的地址,进而建立哈希表格,然后利用哈希函数来查找到各个键值存放在表格中的地址。简单来说,就是把一些复杂的数据,通过某种函数映射(与数学中的映射概念一样)关系,映射成更加易于查找的方式。哈希查找算法的查找速度与数据多少无关,完美的哈希查找算法一般都可以做到一次读取完成查找。
就像生活中,要想找到自己想要的物品,最好的办法就是把该物品固定在某个地方,每次需要用到它的时候就去对应的地方找,用完之后再放回原处。哈希查找法就是这样的一种算法,例如,在一本书中查找内容,首先翻开这本书的目录,然后在目录上找到想要的内容,最后直接根据对应的页码就能找到所需要的内容。
哈希查找算法具有保密性高的特点,因此哈希查找算法常被应用在数据压缩和加解密方面。常见的哈希算法有除留取余法、平方取中法以及折叠法。在讲解这三种算法之前,首先需要了解 哈希表 和 哈希函数 的概念。
1. 哈希表和哈希函数
哈希表是存储键值和键值所对应地址的一种数据集合。哈希表中的位置,一般称为槽位,每个槽位都能保存一个数据元素并以一个整数命名(从 0 开始)。这样我们就有了0号槽位、1号槽位等。起始时,哈希表里没有数据,槽位是空的,这样在构建哈希表时,可以把槽位的值都初始化成 None,如下图所示。

这是一个大小为 11 的哈希表,或者说有 n 个槽位的哈希表,n 为0~10。上图中的元素和保存的槽位之间的映射关系,称为哈希函数。哈希函数接受一个元素作为参数,返回一个0到n-1的整数作为槽位名。说明:每种哈希算法的哈希函数和哈希表,会在每种哈希算法中介绍。
2. 除留余数法
除留余数法是哈希算法中最简单的一种算法。它是将每个数据除以某个常数后,取余数来当索引。除留取余法所对应的哈希函数形式如下:
h(item)=item % num
参数说明:
- item:每个数据。
- num:一个常数,一般会选择一个质数,如下面的例子中取质数 11。
例如,将整数集:54、26、93、17、77、31 中每个数据都除以 11,所得的余数作为哈希值,哈希值如下表所示。
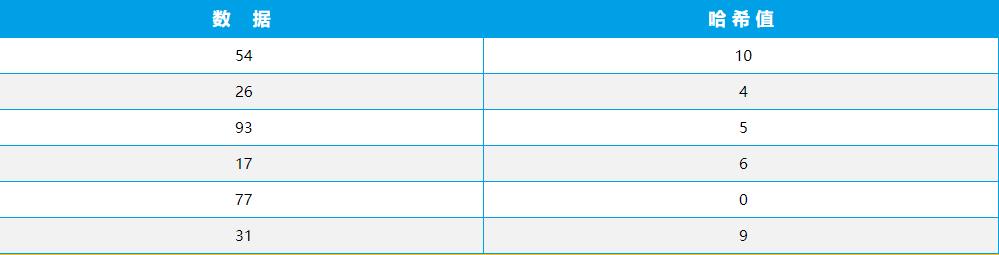
注意:除留余数法一般以某种形式存于所有哈希函数中,因为它的运算结果一定在槽位范围内。哈希值计算出来之后,就要把元素插入到哈希表中指定的位置,如下图所示。

则对应的哈希函数也得到了哈希值,如:h(54)=10,h(26)=4,h(93)=5,h(17)=6,h(77)=0,h(31)=9。
3. 折叠法
对给定的数据集,哈希函数将每个元素映射为单个槽位,称为 完美哈希函数。但是对于任意一个数据集合,没有系统能构造出完美哈希函数。例如,在上述除留余数法的例子中再加上一个数据 44,该数字除以 11 后,得到的余数是 0,这与数据 77 的哈希值相同。遇到这种情况时,解决办法之一就是扩大哈希表,但是这种做法太浪费空间。因此又有了扩展除留取余数的方案,也就是折叠法。
折叠法是将数据分成一串数据,先将数据拆成几部分,再把它们加起来作为哈希地址。例如,有这样一串数据:5205211314,将这串数据中的数字两两分一组,如下图所示:

然后将拆的数据进行相加,如下图所示:
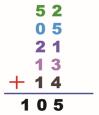
相加之后得到的数值就是这串数据的哈希地址,如果设定槽位是 11,用除留余数法将哈希地址除以 11,得到的值是 6,而数据 6 就是这串数据的哈希值,这种做法称为 移动折叠法。
有些折叠法多了一步,就是在相加之前,对数据进行奇数或偶数反转,再将反转后的数字相加。下图所示就是将奇数反转的过程,再将反转后的数据相加,得到的 159 也称为哈希地址。
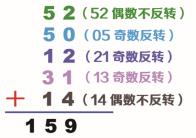
此时设定槽位是 11,将哈希地址除以 11,得到的值是 5,数据 5 就是这个数据的哈希值。接下来介绍将偶数反转的情况,如下图所示。

将上图中反转后的数据相加,得到的 105 也称为哈希地址。如果设定槽位是 11,除留余数法将哈希地址除以 11,得到的值是 6,数据 6 就是这个数据的哈希值。奇数/偶数反转这种折叠法称为 边界折叠法。
4. 平方取中法
平方取中法是先将各个数据平方,将平方后数据取中间的某段数字作为索引,例如,对于整数集 54,26,93,17,77,31,平方取中法如下:
步骤1:先将各个数据平方,得到的值如下:
54=2916
26=676
93=8649
17=289
77=5929
31=961
步骤2:取以上平方值的中间数,即取十位和百位,得到该整数集中数据的哈希地址分别为:
91 67 64 28 92 96
步骤3:若设置槽位是 11,将步骤 2 得到的数据分别除以 11 留余数,得到的哈希值分别为:
3 1 9 6 4 8
得到的对应关系如下图所示:

5. 碰撞与溢出问题
哈希算法的理想情况是所有数据经过哈希函数运算后得到不同的值,但是在实际情况中即使得到的哈希值不同,也有可能得到相同的地址,这种问题被称为 碰撞问题。使用哈希算法,将数据放到哈希表中存储数据的对应位置,若该位置满了,就会溢出,这种问题被称为 溢出问题。存在问题就需要解决问题,如何解决碰撞问题与溢出问题很重要。由于常见的解决问题方法有多种,故在后续博文中进行更新。
实例:用哈希查找算法查找七色光颜色。具体代码如下:
class HashTable(object): # 创建哈希表
def __init__(self):
self.size = 11 # 哈希表长度
self.throw = [None] * self.size # 哈希表数据键初始化
self.data = [None] * self.size # 哈希表数据值初始化
# 假定最终将有一个空槽,除非 key 已经存在于 self. throw中。它计算原始
# 哈希值,如果该槽不为空,则迭代 rehash 函数,直到出现空槽。如果非空槽已经包含key,
# 则旧数据值将替换为新数据值
def put(self, key, value): # 输出键值
hashvalue = self.hashfunction(key, len(self.throw)) # 创建哈希值
if self.throw[hashvalue] is None:
self.throw[hashvalue] = key # 将key值给哈希表的throw
self.data[hashvalue] = value # 将value值给哈希表的data
else:
if self.throw[hashvalue] == key:
self.data[hashvalue] = value
else:
nextslot = self.rehash(hashvalue, len(self.throw))
while self.throw[nextslot] is not None and self.throw[nextslot] != key:
nextslot = self.rehash(nextslot, len(self.throw))
if self.throw[nextslot] is None:
self.throw[nextslot] = key
self.data[nextslot] = value
else:
self.data[nextslot] = value
def rehash(self, oldhash, size):
return (oldhash + 1) % size
def hashfunction(self, key, size):
return key % size
# 从计算初始哈希值开始。如果值不在初始槽中,则 rehash 用
# 于定位下一个可能的位置。
def get(self, key):
startslot = self.hashfunction(key, len(self.throw))
data = None
found = False
stop = False
pos = startslot
while pos is not None and not found and not stop:
if self.throw[pos] == key:
found = True
data = self.data[pos]
else:
pos = self.rehash(pos, len(self.throw))
# 回到了原点,表示找遍了没有找到
if pos == startslot:
stop = True
return data
# 重载载 __getitem__ 和 __setitem__ 方法以允许使用 [] 访问
def __getitem__(self, key):
return self.get(key)
def __setitem__(self, key, value):
return self.put(key, value)
H = HashTable() # 创建哈希表
H[16] = "红" # 给哈希表赋值
H[28] = "橙"
H[32] = "黄"
H[14] = "绿"
H[56] = "青"
H[36] = "蓝"
H[71] = "紫"
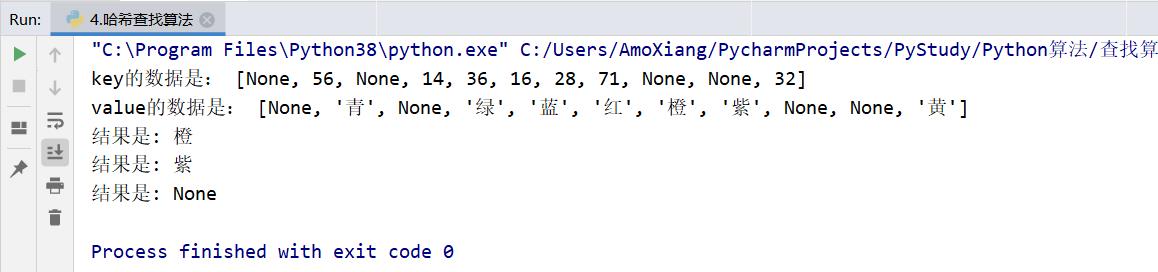
print("key的数据是:", H.throw) # 输出键key
print("value的数据是:", H.data) # 输出值value
print("结果是:", H[28]) # 根据key=28查value
print("结果是:", H[71]) # 根据key=71查value
print("结果是:", H[93]) # 根据key=93查value
程序执行结果如下图所示:
五、分块查找算法
分块查找是二分法查找和顺序查找的改进方法,分块查找要求索引表是有序的,对块内结点没有排序要求,块内结点可以是有序的也可以是无序的。
分块查找就是把一个大的线性表分解成若干块,每块中的节点可以任意存放,但块与块之间必须排序。与此同时,还要建立一个索引表,把每块中的最大值作为索引表的索引值,此索引表需要按块的顺序存放到一个辅助数组中。查找时,首先在索引表中进行查找,确定要找的结点所在的块。由于索引表是排序的,因此,对索引表的查找可以采用顺序查找或二分查找;然后,在相应的块中采用顺序查找,即可找到对应的结点。
例如,有这样一列数据:23、43、56、78、97、100、120、135、147、150。如下图所示:

想要查找的数据是 150,使用分块查找法步骤如下:
步骤1:将上图所示的数据进行分块,按照每块长度为 4 进行分块,分块情况如下图所示:

说明:每块的长度是任意指定的,博主在这里用的长度为4,读者可以根据自己的需要指定每块长度。
步骤2:选取各块中的最大关键字构成一个索引表,即选取上图所示的各块的最大值,第一块最大的值是 78,第二块最大的值是 135,第三块最大值是 155,形成的索引表如下图所示:
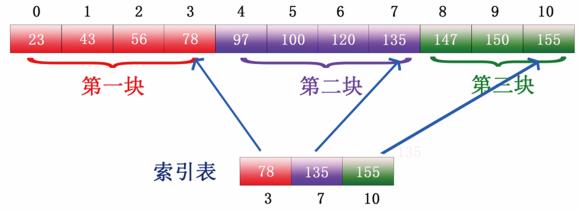
步骤3:用顺序查找或者二分查找判断想要查找数据 150 在上图所示的索引表中的哪块内容中,这里博主用的是二分查找法,即先取中间值 135 与 150 比较,如下图所示:
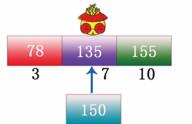
步骤4:结果是中间位置的数据 135 比目标数据 150 小,因此目标数据在 135 的下一块内。将数据定位在第 3 块内,此时将第 3 块内的数据取出,进行顺序比较,如下图所示:

步骤5:通过顺序查找第 3 块的内容,终于在第 9 个位置找到目标数,此时分块查找结束。
总结:至此,分块查找算法已经讲解完毕。通过和二分查找法和顺序查找法对比来看,分块查找的速度虽然不如二分查找算法,但比顺序查找算法快得多。当数据很多且块数很大时,对索引表可以采用二分查找,这样能够进一步提高查找的速度。
实例:实现分块查找算法。具体代码如下:
def search(data, key): # 用二分查找 想要查找的数据在哪块内
length STL六大组件之算法