图像识别基于模板匹配车牌识别matlab源码

Posted 2021-05-24 Matlab走起

一、简介

1.模板匹配基本原理概述

 

      当我们比较两幅图像的时候，首先面对的基本问题是：什么时候两幅图像才是一样或比较相似的，这两幅图像的相似程度如何衡量？当然，比较一般的方法是，当两幅图像的所有像素灰度值一样的时候，我们认为这样幅图是一样的。这种比较方法在某些特定的应用领域是可行的，比如在恒定光照环境和相机内部环境下，检测连续两帧图像的变化。简单的比较像素之间的差值在大多数应用场合下是不太合适的。噪声、量化误差、微小的光照变化、极小的平移或旋转在两幅图像像素简单差值的时候将产生较大的像素差值，但是人眼观察看来，两幅图像仍然是一样的。显然，人类知觉能够感应更为广泛的相似性内容，即使在单个像素差值较大的情况下，也能够利用诸如结构和图像内容来识别两幅图像的相似性。在结构或语义层面比较图像是一个比较困难的问题，同时也是一个比较有趣的研究领域。

      在这我们介绍的是一种在像素层面相对简单的图像比较方法。即在一幅较大图像定位一幅给定的子图像-----模板图像，即通常所说的模板匹配。这种情况经常发生，比如在一个图像场景中定位一个特定的物体，或者是在图像序列中追踪最某些特定模式。模板匹配的基本原理很简单：在待搜寻的图像中，移动模板图像，在每一个位置测量待搜寻图像的子图像和模板图像的差值，当相似度达到最大时，记录其相应的位置。但实际情况却不是这么简单，如何选取合适的距离测量方法？当亮度或对比度改变时应该如何处理？匹配中总的距离差值为多少才可以被认为是相似度比较高？这些问题都需要根据实用情况加以考虑。

 

 

     以上图像都“相同”吗？在原始图像（a）和其他五幅图像(b-f)中,简单的比较图像像素间的差值将会得到较大的距离值。

 

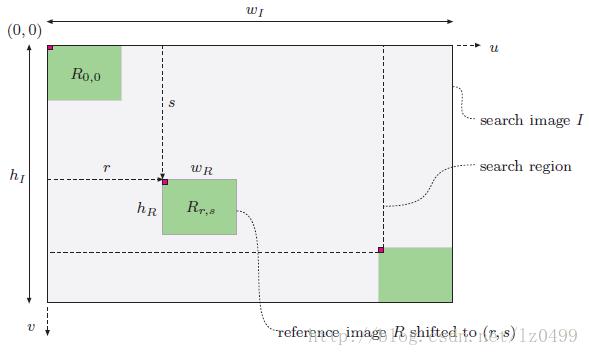
       模板匹配的基本原理。以两幅图像的原点为参考点，参考图像R在待搜寻的图像I中平移（r,s）个单位，待搜寻图像的大小和模板图像的大小确定的最大的搜寻区域。

 

2.灰度图像中的模板匹配

 

 

     灰度图像中的模板匹配，主要是找到模板图像R和搜寻图像I中的子图像相同或最相似的位置。以下式子表示模板在原始图像偏移（r,s）单位，

 

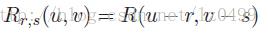
    参考图像R分别在水平方法和竖直方向平移r和s个单位，那么模板匹配的问题可以概述为：

   给定搜寻图像I和模板图像R。找到平移后的参考图像以及搜寻图像中所对应的子图像相似度最大的位置。

 

2.1图像匹配中的距离函数

 

 

   模板匹配中最重要的是找到一种对灰度和对比度变化具有较好鲁棒性的相似度测量函数。

    为了测量图像间的相似度程度，我们计算每一次平移（r,s）后的参考图像和搜寻图像中所对应的子图像的“距离”d(r,s)（如下图所示）。二维灰度图像中的测量函数有如下基本的几种：

 

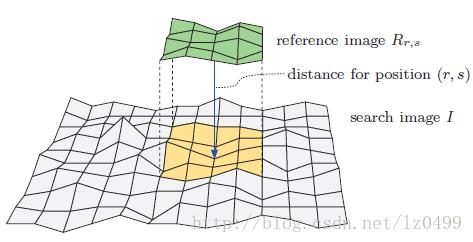
二维图像中距离测量函数的表示

 

 

Sum ofabsolute differences:

 

Maximumdifference:

                                                                

 

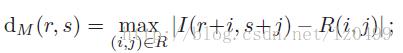
Sum ofsquared differences:

                                                                                    

 

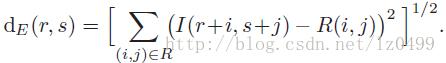
由于SSD函数的特性，在统计和最优化领域被经常用到。为了找到参考图像在搜寻图像中的最佳匹配位置，只要使得SSD函数取得最小值即可。即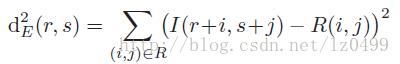    

 

 

 

 

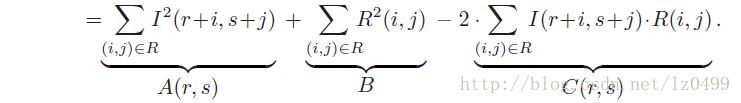
         上式中的B是参考图像中所有像素灰度值的平方和，是一个常量（独立于r,s）因此在计算其最小值的时候可以忽略。A(r,s)表示的是搜寻图像在（r,s）的子图像中所有像素灰度值的平方和，C(r,s)即称为搜寻图像和参考图像的线性互相关函数，通常可以表示为：

                                                              

 

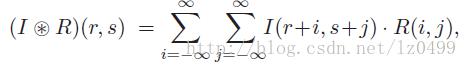
     当R 和I超出边界时，其值为零，故上式亦可表示为：

 

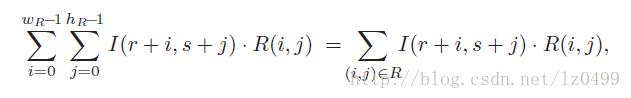
      如果我们假设A(r,s)在搜寻图像中是一个常量，那么SSD中计算其最佳匹配位置的时候，其值是可以忽略的，且当C(r,s)取得最大值的时候，参考图像和搜寻图像中的子图像最相似。这种情况下，SSD的最小值可以通过计算C(r,s)的最大值获得。

2.2归一化的互相关

 

    实际应用当中，上述假定A(r,s)为一常量并不总是成立。因此，上述的互相关的结果将随着搜寻图像中像素灰度值的改变而产生较大变化。归一化的互相关把参考图像和当前的子图像的能量考虑进去：

 

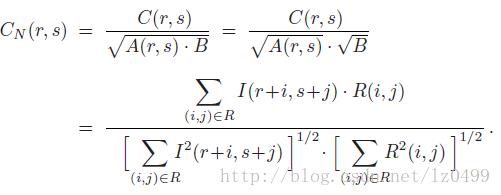
     当参考图像和搜寻图像子图像灰度值都是正数的时候，Cn(r,s)的值总是为[0,1]范围内，与图像其他像素灰度值无关。当Cn(r,s)等于1时，表明在平移位置（r,s），参考图像和子图像达到最大相似度；相反，当Cn(r,s)等于0时，表明在平移位置（r,s），参考图像和子图像完全不匹配。当子图像中的所有灰度值改变时，归一化的互相关Cn(r,s)也会极大的改变。

 

2.2相关系数

 

 

    为了解决上述问题，我们引入子图像和模板图像中的灰度平均值。上述归一化函数可以改写为：

 

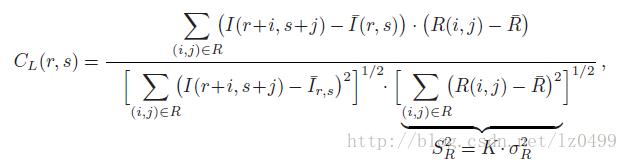
   子图像和参考图像平均值分别定义为：

 

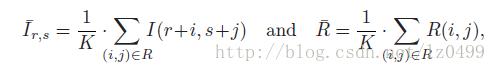
    其中，K表示参考图像中像素的数量。在统计学中，上述表达式被称为相关系数。然而，与统计学中作为全局测量方法不同的是，CL（r,s）被定义是一个局部的测量函数。CL（r,s）的值域范围为[-1,1]。当CL(r,s)等于1时，表明在平移位置（r,s），参考图像和子图像达到最大相似度；相反，当CL(r,s)等于0时，表明在平移位置（r,s），参考图像和子图像完全不匹配。表达式：

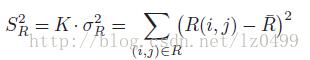
表示的是K倍模板图像R中像素灰度值方差，这是一个常量，只需要计算一次即可。由于方差存在如下关系：（具体可参考http://imagej.net/Integral_Image_Filters）

 

 

        具体推到如下所示：

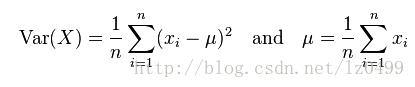
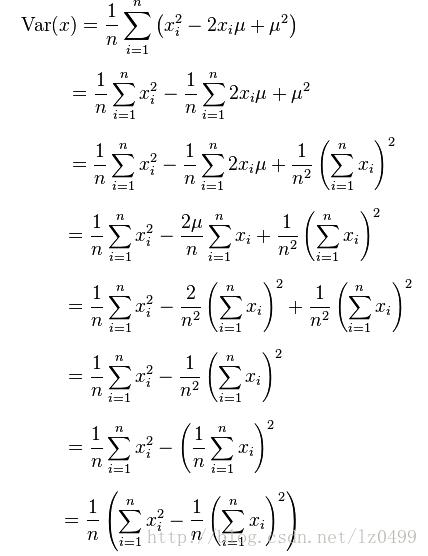
     因此，可以SR改写为

 

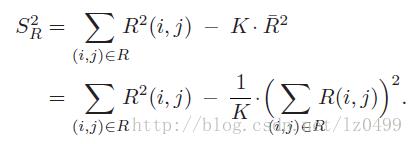
  带入到CL(r,s)，可得：

 

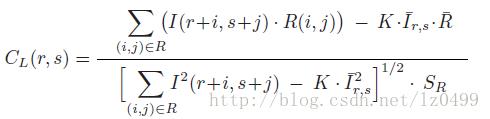
  由此，可得到一个高效的计算相关系数的方法。

二、源代码

% clear 
addpath(genpath(pwd)); %添加子文件夹下的所有文件
%%加载图像
start=6212;
% state=num+1;
% start=6540;
state=1;
 
% for num = state:294
    close all
num = 1  ;   %读取文件夹下的第num张图片 
% 20
% 
 
    fname=['样本库\\IMG_',num2str(start+num),'.jpg'];
   % 有三个车牌文件夹：'PlateImages/%d.jpg' 或者'PlateImages/Image1/%d.jpg' 或'PlateImages/Image2/%d.jpg'
filename = fullfile(pwd, fname);
Img = imread(filename);
%{
figure(5);
subplot(2,2,1);imshow(Img);title('原图');I1=rgb2gray(Img);
subplot(2,2,2);imshow(I1);title('灰度图');
subplot(2,2,3);imhist(I1);title('灰度图直方图');I2=edge(I1,'roberts',0.15,'both');
subplot(2,2,4);imshow(I2);title('roberts算子边缘检测')
se=[1;1;1];
I3=imerode(I2,se);
figure(6);
subplot(2,2,1);imshow(I3);title('腐蚀后图像');se=strel('rectangle',[25,25]);I4=imclose(I3,se);
subplot(2,2,2);imshow(I4);title('平滑图像的轮廓');I5=bwareaopen(I4,2000);
subplot(2,2,3);imshow(I5);title('从对象中移除小对象');
%} 
 
GetDB;
 
%% 定位车牌
% 定位车牌：找出车牌在原始图片中的位置
% 输入参数Img：  读取的原始真彩色图像信息
% 输出参数plate：经过定位处理后，从原始真彩色图像(会进行压缩处理)截取到的车牌位置处的真彩色图像信息
plate = Pre_Process(Img);
 
%% 倾斜校正
% 倾斜校正：对待识别数字的倾斜校正，分别使用Radon变换和仿射函数处理水平倾斜校正和垂直倾斜校正
% 输入参数：plate为定位截取的真彩色车牌图像信息
% 输出参数：
plate = radon_repair(plate);
 
%% 车牌滤波
% 车牌滤波：剔除(像素值置0)车牌图片的边界图像信息
% 输入参数：plate为定位截取的真彩色车牌图像信息
% 输出参数：d为原始车牌图像滤波(即剔除上下边界外(和使用多边形区域剔除))后的图片，p为真彩色原始车牌图像plate逆时针旋转后的图片
[d, p] = Plate_Process(plate,fname);
 
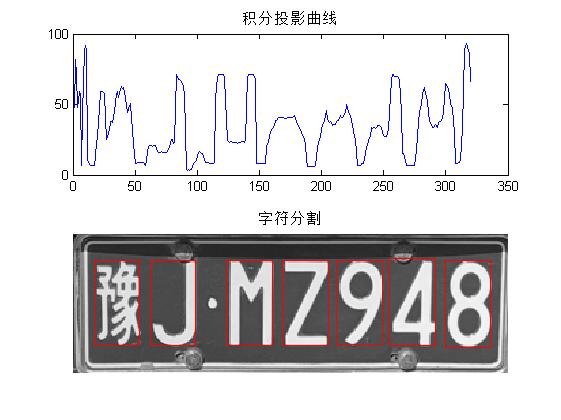
%% 分割车牌
% 分割车牌：裁掉(删除)车牌图像信息的边界
% 输入参数：d为原始车牌图像滤波(即剔除上下边界外(和使用多边形区域剔除))后的图片，p为真彩色原始车牌图像plate逆时针旋转后的图片
% 输出参数：根据图像d的非0边界，裁剪出的输入图片：输入图片d裁剪后输出图片e，输入图片p裁剪后输出图片p
[e, p] = Segmation(d, p);
%% 去除噪声
function [result, plate] = Plate_Process(plate, fname, flag)
    % 分割步骤
    if nargin < 3
        flag = 1;
    end
    % n = ndims(A) returns the number of dimensions in the array A.
    if ndims(plate) == 3
        % I = rgb2gray(RGB) converts the truecolor image RGB to the grayscale intensity image I.
        % rgb2gray converts RGB images to grayscale by eliminating the hue and saturation information while retaining the luminance.
        plate1 = rgb2gray(plate);   % 将车牌原始图片信息转换成grayscale intensity image(灰度图像？为方便，下面都称为灰度图像)
    else
        plate1 = plate;
    end
    Im = plate1;    % Im为灰度图像
    plate = double(plate);
    % B = mean2(A) computes the mean of the values in A.
    % b = std2(A) computes the standard deviation of the values in A.
    % 求出当前图片的[均值 标准差]矩阵，用于和数据库的[均值 标准差]矩阵进行计算，然后找出最适合用于处理当前图片的数据库参数信息
    m = [mean2(plate(:,:,1)) mean2(plate(:,:,2)) mean2(plate(:,:,3)) std2(plate(:,:,1)) std2(plate(:,:,2)) std2(plate(:,:,3))];
    
    % f = fullfile(filepart1,...,filepartN) builds a full file specification, f, from the folders and file names specified.
    % f = fullfile('myfolder','mysubfolder','myfile.m') ===> f = myfolder\\mysubfolder\\myfile.m
    load('model.mat');
    
    ms = cat(1, M.m);   % 数据库中的[均值 标准差]矩阵
    
    % B = repmat(A,m,n) creates a large matrix B consisting of an m-by-n tiling of copies of A.
    % The size of B is [size(A,1)*m, (size(A,2)*n]. The statement repmat(A,n) creates an n-by-n tiling.
    m = repmat(m, size(ms, 1), 1);  % 将当前图片的[均值 标准差]矩阵进行拓展，以便进行与数据库[均值 标准差]矩阵运算
    
    % B = sum(A,dim) sums along the dimension of A specified by scalar dim. The dim input is an integer value from 1 to N, 
    % where N is the number of dimensions in A. Set dim to 1 to compute the sum of each column, 2 to sum rows, etc.
    % 按行求和
    dis = sum((m - ms).^2, 2);  % 当前图片[均值 标准差]矩阵与数据库[均值 标准差]矩阵的方差
    [~, id] = min(dis);         % 找出方差最小的那个，也就是说，找出最适合用于处理当前图片的数据库参数
    if fname(6)=='s'
        ro = M(id).ro;              % 图片旋转的角度参数，单位为度
    else
        ro=0;
    end
    th = M(id).th;              % 将灰度图像转换为二进制图像的门限，灰度图像中的值大于该门限则转换为1，否则转换为0
    pts = M(id).pts;            % 定义图片的顶点
    
    % B = imrotate(A,angle,method) rotates image A by angle degrees in a counterclockwise direction around its
    % center point, using the interpolation method specified by method.
    Im = imrotate(Im, ro, 'bilinear');          % 将灰度图片Im按照逆时针方向，旋转ro度，插值方法选择双线性插值
    plate = imrotate(plate, ro, 'bilinear');    % 将车牌原始图像，也按照逆时针方向，旋转ro度，插值方法选择双线性插值
    
    % BW = im2bw(I, level) converts the grayscale image I to a binary image. 
    % The output image BW replaces all pixels in the input image with luminance(亮度) greater than level with the value 1 (white)
    % and replaces all other pixels with the value 0 (black). Specify level in the range [0,1]. This range is relative to
    % the signal levels possible for the image's class. Therefore, a level value of 0.5 is midway between black and white, regardless of class.
    bw = im2bw(Im, th);     % 将灰度图像Im转换成二进制图像，转换门限为th
    
    % h = fspecial('average', hsize) returns an averaging filter h of size hsize.
    % The argument hsize can be a vector specifying the number of rows and columns in h, or it can be a scalar, in which case h is a square matrix.
    h = fspecial('average', 2);     % 定义一个多维均值滤波器h，维度为2 x 2
    
    % B = imfilter(A,h) filters the multidimensional array A with the multidimensional filter h.
    % The array A can be logical or a nonsparse numeric array of any class and dimension. The result B has the same size and class as A.
    % ___= imfilter(___,options,...) performs multidimensional filtering according to the specified options.
    % 'replicate' ===> Input array values outside the bounds of the array are assumed to equal the nearest array border value.
    bw1 = imfilter(bw, h, 'replicate');     % 使用多维均值滤波器h，对二进制图像bw进行滤波，滤波选项为replicate
    
%     mask = Mask_Process(bw1);   % 此方法功能是去除bw1图像的上下杂线，即使用特定算法，剔除二进制图像bw1的上下边界处的信息(这些行的像素值全设为0)
                                % 此处的mask可理解为：如果图像像素点在杂线上边界与车牌上边界之间或杂线下边界与车牌下边界之间，则这个像素点的值为0，
                                % 否则，如果图像像素点在杂线上边界和杂线下边界之间，则这个像素点的值为1
%     bw2 = bw1 .* mask;          % 这个.*操作可理解为：与运算，这样bw2就是利用mask矩阵剔除二进制图像bw1中干扰后的结果
    bw2 = bw1;
    
    % 除了通过Mask_Process()函数剔除杂线外，如果有定义车牌边界信息，则可进一步使用车牌边界信息进行图像处理
%     if ~isempty(pts)            % 如果pts不空(即，有外部边界顶点定义)，则执行
%         % BW = roipoly(I, c, r) returns the region of interest(ROI) specified by the polygon(多边形) described by vectors c and r,
%         % which specify the column and row indices of each vertex(顶点), respectively. c and r must be the same size.
%         % 根据二进制图片bw2，以及多边形的顶点pts(:, 1), pts(:, 2)，得到二进制图像mask，顶点围起来的区域的值全为1，
%         % 其它区域的值全为0，这样做的目的是剔除车牌边界的干扰
%         mask = roipoly(bw2, pts(:, 1), pts(:, 2));      % 得到一个由pts顶点(可组成多边形)指定的二进制边界图像
%         bw1 = bw1 .* mask;      % bw1是只使用多边形剔除干扰后的二进制图像
%         bw2 = bw2 .* mask;      % bw2是使用Mask_Process()算法和多边形两种方法剔除干扰后的二进制图像
%     end

三、运行结果

四、备注

完整代码或者仿真添加QQ1575304183