图像融合基于区域的空间域图像融合

Posted 2021-05-24 Matlab走起

先对源图像作小波分解，低频分量加权平均，高频分量用模糊C均值聚类算法进行区域分割，对区域进行基于ssim值的融合，最后小波逆变换得到融合图像。

  小波指的是一种能量在时域非常集中的波，它的能量有限，都集中在某一点附近，而且积分的值为零，这说明它与傅里叶波一样是正交波。

    图像的傅里叶变换是将图像信号分解为各种不同频率的正弦波。同样，小波变换是将图像信号分解为由原始小波位移和缩放之后的一组小波。小波在图像处理里被称为图像显微镜，原因在于它的多分辨率分解能力可以将图片信息一层一层分解剥离开来。剥离的手段就是通过低通和高通滤波器。

     小波变换可以和傅里叶变换结合起来理解。傅里叶变换是用一系列不同频率的正余弦函数去分解原函数，变换后得到是原函数在正余弦不同频率下的系数。小波变换使用一系列的不同尺度的小波去分解原函数，变换后得到的是原函数在不同尺度小波下的系数。不同的小波通过平移与尺度变换分解，平移是为了得到原函数的时间特性，尺度变换是为了得到原函数的频率特性。

小波变换步骤：

1.把小波w(t)和原函数f(t)的开始部分进行比较，计算系数C。系数C表示该部分函数与小波的相似程度。

2.把小波向右移k单位，得到小波w(t-k)，重复1。重复该步骤直至函数f结束.

3.扩展小波w(t)，得到小波w(t/2)，重复步骤1,2.

4.不断扩展小波，重复1,2,3.

haar小波：

我这里使用的haar小波，缩放函数是[1 1]，小波函数是[1 -1]。是最简单的小波了。

图像二维离散小波变换 ：

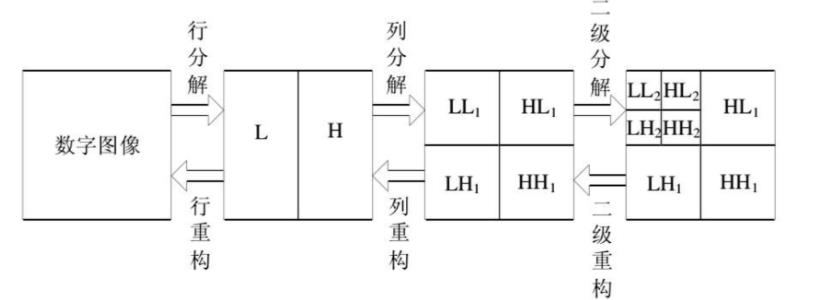
     图像的二维离散小波分解和重构过程如下图所示，分解过程可描述为：首先对图像的每一行进行 1D-DWT，获得原始图像在水平方向上的低频分量 L 和高频分量 H，然后对变换所得数据的每一列进行 1D-DWT，获得原始图像在水平和垂直方向上的低频分量 LL、水平方向上的低频和垂直方向上的高频 LH、水平方向上的高频和垂直方向上的低频 HL 以及水平和垂直方向上的的高频分量 HH。

    重构过程可描述为：首先对变换结果的每一列进行以为离散小波逆变换，再对变换所得数据的每一行进行一维离散小波逆变换，即可获得重构图像。由上述过程可以看出，图像的小波分解是一个将信号按照低频和有向高频进行分离的过程，分解过程中还可以根据需要对得到的 LL 分量进行进一步的小波分解，直至达到要求。

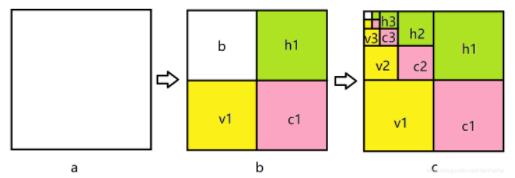
对于二维图像Haar变换不再从一个方向进行滤波，而是从水平和竖直两个方向进行低通和高通滤波（水平和竖直先后不影响），用图像表述如图所示：图中a表示原图，图b表示经过一级小波变换的结果，h1 表示水平反向的细节，v1 表示竖直方向的细节，c1表示对角线方向的细节，b表示下2采样的图像。图c中表示继续进行Haar小波变换。一级Haar小波变换实际效果如图3所示

                      

clear all;
close all;
clc;
I1=imread('a.tif');
I1=rgb2gray(I1);
I2=imread('b.tif');
I2=rgb2gray(I2);
F=bbsd_fuse(I1,I2);
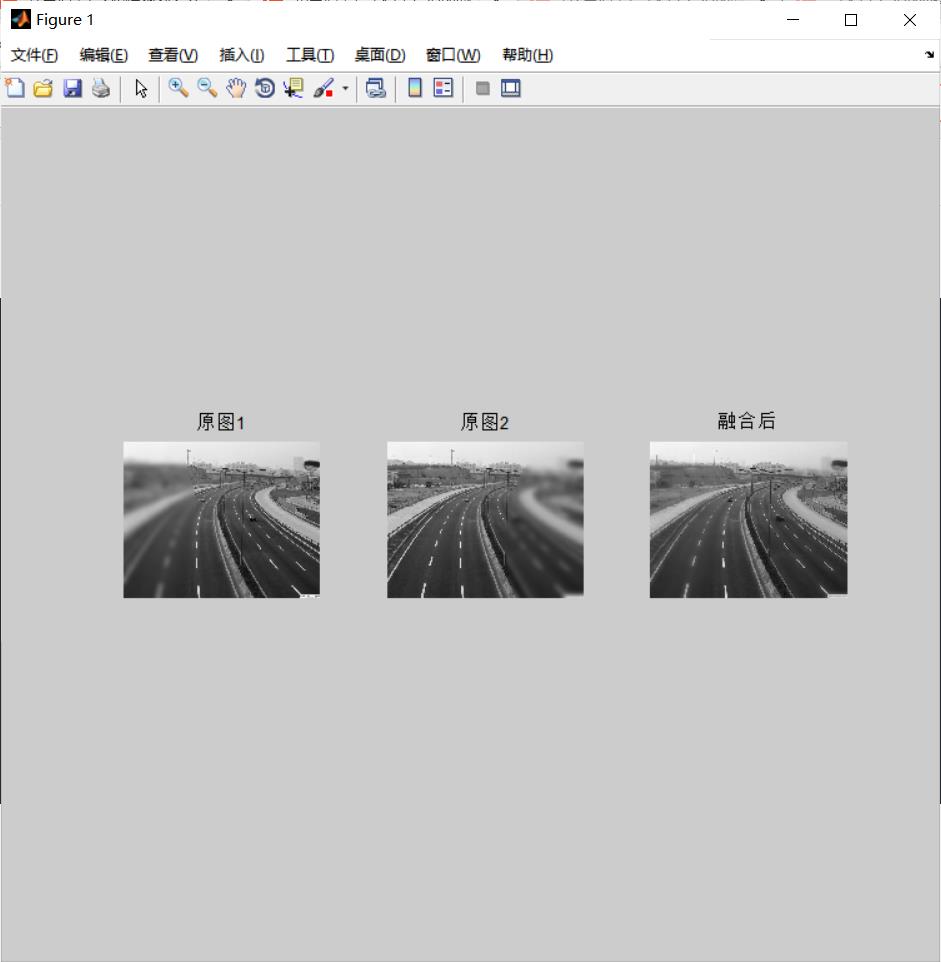
figure(1)
subplot(131)
imshow(I1);
title('原图1')
subplot(132)
imshow(I2);
title('原图2')
subplot(133)
imshow(F);
title('融合后')

完整代码或者仿真咨询添加QQ1575304183