图像融合基于matlab多分辨率奇异值分解图像融合含Matlab源码 2374期
Posted 海神之光
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图像融合基于matlab多分辨率奇异值分解图像融合含Matlab源码 2374期相关的知识,希望对你有一定的参考价值。
⛄一、多分辨率奇异值分解图像融合简介
0 引言
图像融合[1,2]是指将多分辨率或多介质图像数据通过空间配准和图像信息互补产生新的图像的综合分析技术。图像融合一般分为像素级、特征级和决策级融合, 而多分辨率图像融合算法则是一类非常重要的像素级融合算法。
对多分辨率图像融合的研究, 最初始于文献[3]中Burt和Adelson提出的拉普拉斯金字塔算法。金字塔分解符合人眼视觉系统在处理视觉信号时具有多分辨率的特性, 但其层间分解量之间具有相关性, 且没有严格的理论基础的支撑。随着小波变换理论[4,5]的提出和完善, 小波变换在图像融合领域得到了广泛的应用。文献[6]中Li Hui等提出小波变换应用于图像融合的代表性方法。文献[7]中Chipman等提出采用离散小波变换进行图像融合处理。文献[8-9]都提出了基于小波的图像融合算法, 文献[10]在文献[3, 9]的基础上提出了基于金字塔的多曝光图像融合。
由于离散小波变换在提取图像低频信息的同时, 又能获得三个方向的高频细节信息, 在理论上比传统的金字塔融合方法具有更好的效果, 且在分解层次上会提供方向信息;并且小波变换在不同的分辨率中都含有独特的信息, 具有良好的时域和频域局部性以及多分辨性。但是基于离散小波分解的图像融合算法缺乏平移不变性, 这使得融合结果中出现了伪影, 降低了融合图像的质量。小波变换的冗余度非常高, 这是小波固有的缺陷。同时, 小波基的选取[11]也是小波变换的难点之一。
文中提出一种新的基于多分辨率奇异值分解 (MSVD) 的算法融合源图像, 用MSVD得到的结果与基于小波图像融合的结果进行比较。
1 SVD的多分辨率形式
在离散二进制小波变换中, 信号分别用低通和高通滤波器进行滤波, 每个结果也由两个元素抽取。整个过程在抽取后的低通输出上进行循环重复, 直到得到理想的分解层数和理想效果。多分辨率奇异值分解类似于小波变换, 其基本思想是在平滑分量的每一层上用奇异值分解 (SVD) 来取代滤波[12]。
1.1 一维情况
令X=[x (1) , x (2) , …, x (N) ]表示一个有限长度的一维信号。假设L≥1, 且N可以整除2L。对矩阵中的值进行重新排列, 使得矩阵第一行包含奇数项值, 第二行包含偶数项值。令重排后的矩阵表示为

下一层的MSVD重复上述过程, 但是用平滑分量Φ1取代X, 并且重复L次。
令Φ0 (1, ·) =X, 使初始平滑分量是原始信号。对于每层l, 向量Φl有Nl=N/2l元素, 表示如下:

l层的MSVD是由式 (3) ~式 (7) 所列方程定义的:
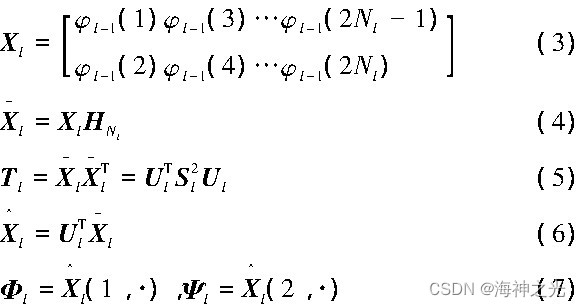
将低分辨率的平滑分量、细节分量和特征向量矩阵Ul存储在一维空间中。因此, 可以将多分辨率奇异值分解写成如下变换:

1.2 二维情况
多分辨率奇异值分解可以在二维或更高维的形式上呈现[13]。本节详细介绍在二维中多分辨率奇异值分解的过程。

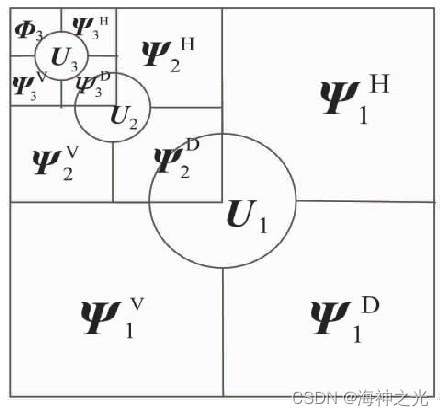
图1 三层MSVD分解结构示例
利用经典参考图像 (pepper图) 做两层的MSVD处理, 其分解示意图如图2所示。为增加可视性, 子图像经过对比度拉伸处理。

图2 分解示意图
2 融合规则
MSVD图像融合方案如图3所示。
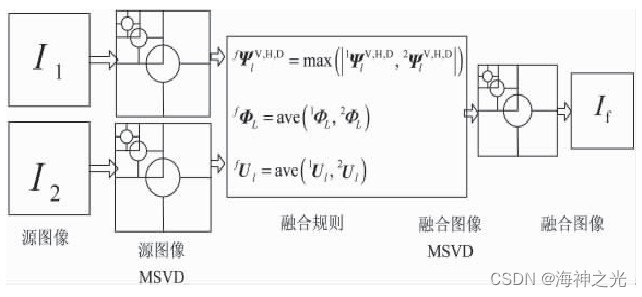
图3 MSVD图像融合方案
文中算法的改进是使用MSVD, 而不是小波或金字塔。被融合的图像I1和I2分别用MSVD分解为l层 (l=1, 2, …, L) 。在每个分解层次中, 细节分量系数对应于图像中更尖锐的亮度变化, 如边缘图像等。而较大的奇异值能更好地保持原始低分辨率图像的有用信息, 因此融合规则将选择两个MSVD细节分量的较大值[14]。对于底层 (l=1) , 融合规则取MSVD平滑分量系数的平均值, 因为底层的平滑分量系数是原始图像的平滑和亚采样版本。融合图像可如下得到:
⛄二、部分源代码
%function[] = msvdfusdemo()
%
% ref: 揑mage Fusion Technique using Multi-resolution Singular Value Decomposition?,
%
close all;
clear all;
home;
% reference image (ground truth)
imt = double(imread(‘saras5t.jpg’));
%images to be fused
im1 = double(imread(‘saras51.jpg’));
im2 = double(imread(‘saras52.jpg’));
%display images to be fused
figure(1); imshow(im1,[]);
figure(2); imshow(im2,[]);
%apply MSVD
[X1, U1] = MSVD(im1);
[X2, U2] = MSVD(im2);
%fusion starts
X.LL = 0.5*(X1.LL+X2.LL);
D = (abs(X1.LH)-abs(X2.LH)) >= 0;
X.LH = D.*X1.LH + (~D).*X2.LH;
D = (abs(X1.HL)-abs(X2.HL)) >= 0;
X.HL = D.*X1.HL + (~D).*X2.HL;
D = (abs(X1.HH)-abs(X2.HH)) >= 0;
X.HH = D.*X1.HH + (~D).*X2.HH;
%XX = [X.LL, X.LH; X.HL, X.HH];
U = 0.5*(U1+U2);
%apply IMSVD
imf = IMSVD(X,U);
%display fused image
figure(3); imshow(imf,[]);
%error image
imd = imt-imf;
figure(4); imshow(imd,[]);
⛄三、运行结果





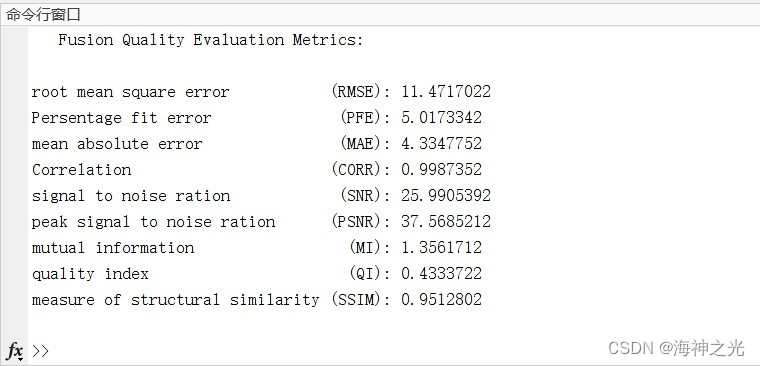
⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]戚曹,朱桂斌,赵林,朱国庆.基于多分辨率奇异值分解的图像融合[J].计算机技术与发展. 2014,24(11)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
以上是关于图像融合基于matlab多分辨率奇异值分解图像融合含Matlab源码 2374期的主要内容,如果未能解决你的问题,请参考以下文章