数据结构之二叉搜索树

Posted 2021-05-24 快乐江湖

文章目录

• 一：二叉搜索树的概念
• 二：二叉搜索树的实现
• • （1）二叉搜索树的插入和查找
  • （2）二叉搜索树的删除
• 三：二叉搜索树的应用

一：二叉搜索树的概念

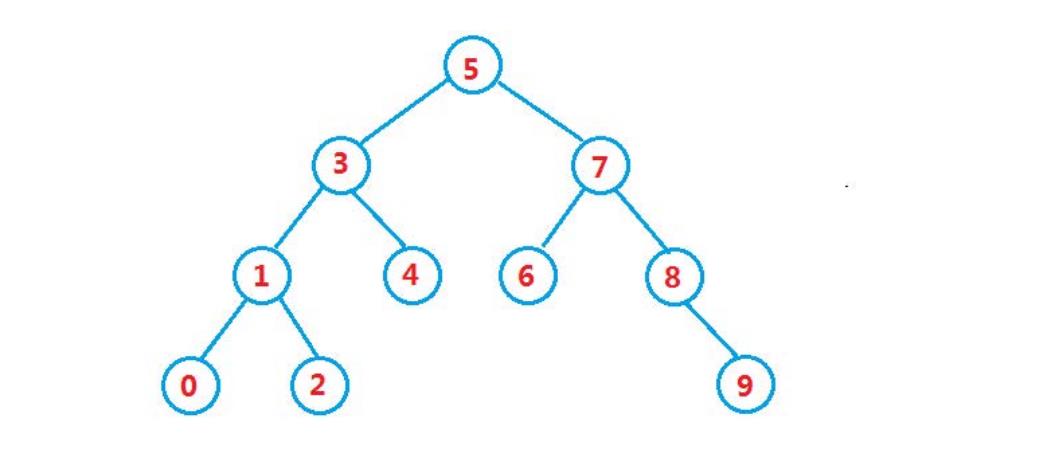
二叉搜索树又称为二叉排序树，它是这样一颗树

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 根节点的左右子树也是一课二叉搜索树

二：二叉搜索树的实现

关于二叉树搜索树的插入和查找都特别简单，这里就不解释了，重点的是二叉树搜索树的删除

（1）二叉搜索树的插入和查找

#pragma once
#include <iostream>
using namespace std;
template <class K>//K表示搜索关键字

struct BSTreeNode
{
	K _key;
	struct BSTreeNode<K>* _left;
	struct BSTreeNode<K>* _right;
	BSTreeNode(const K& key)
		:_key(key)
		,_left(nullptr)
		,_right(nullptr)
	{}
};

template <class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
private:
	Node* _root = nullptr;
public:
	bool insert(const K& key)//二叉搜索树插入
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}
		Node* pre = _root;
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
			{
				cur = cur->_right;
				if (cur == nullptr)
				{
					pre->_right = new Node(key);
					break;
				}
				pre = cur;
			}
			else if(key < cur->_key)
			{
				cur = cur->_left;
				if (cur == nullptr)
				{
					pre->_left = new Node(key);
					break;
				}
				pre = cur;
			}
			else
			{
				return false;
			}
		}

		return true;
	}

	void _Inorder(Node* root)//二叉搜索树中序遍历（即顺序输出），类的递归要写两个
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_key << " ";
		_Inorder(root->_right);
	}
	void Inorder()
	{
		_Inorder(_root);//以便外部调用
		cout << endl;
	}

	Node* Find(const K& key)//二叉搜索树查找
	{
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
			{
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}



};

测试如下

#include "BsTree.h"


void test()
{
	BSTree<int> bs;
	bs.insert(6);
	bs.insert(9);
	bs.insert(2);
	bs.insert(25);
	bs.insert(25);
	bs.insert(84);
	bs.insert(22);
	bs.insert(15);
	bs.insert(93);

	bs.Inorder();

	const BSTreeNode<int>* pb = bs.Find(84);

	if (pb)
	{
		cout << "84找到了" << endl;
	}
	else
	{
		cout << "84没有找到" << endl;
	}
}
int main()
{
	test();
	return 0;

}

（2）二叉搜索树的删除

二叉搜索树的删除稍显麻烦，总的来说要考虑三种情况：叶子结点，某个结点的左子树或右子树为空，某个节点的左子树和右子树都存在

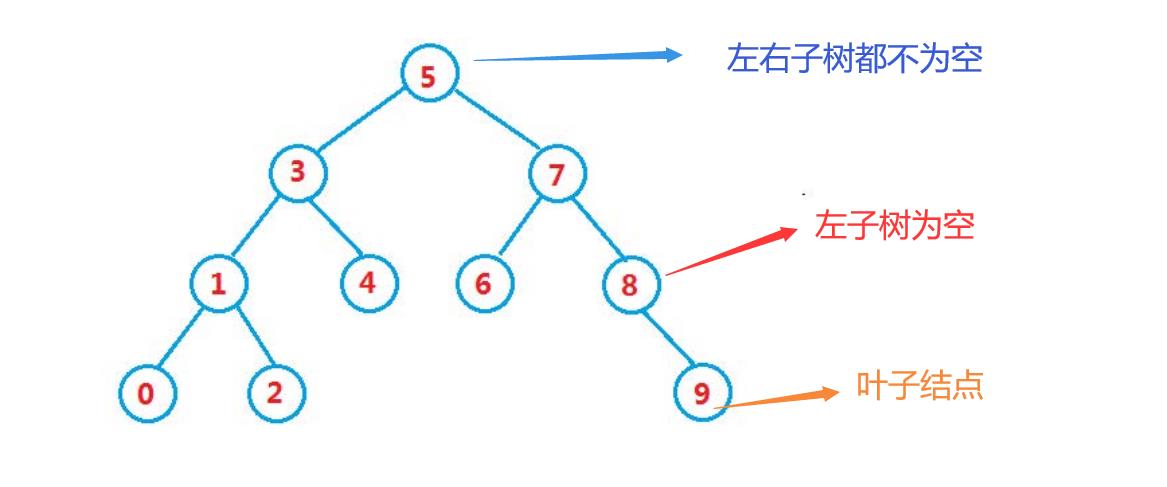
当然叶子结点可以归结为左子树为空或右子树为空那一种情况，因此共有左为空，右为空和左右都不为空这么三种情况。

1：如果左为空，那么让父亲的左或者右指向我的右


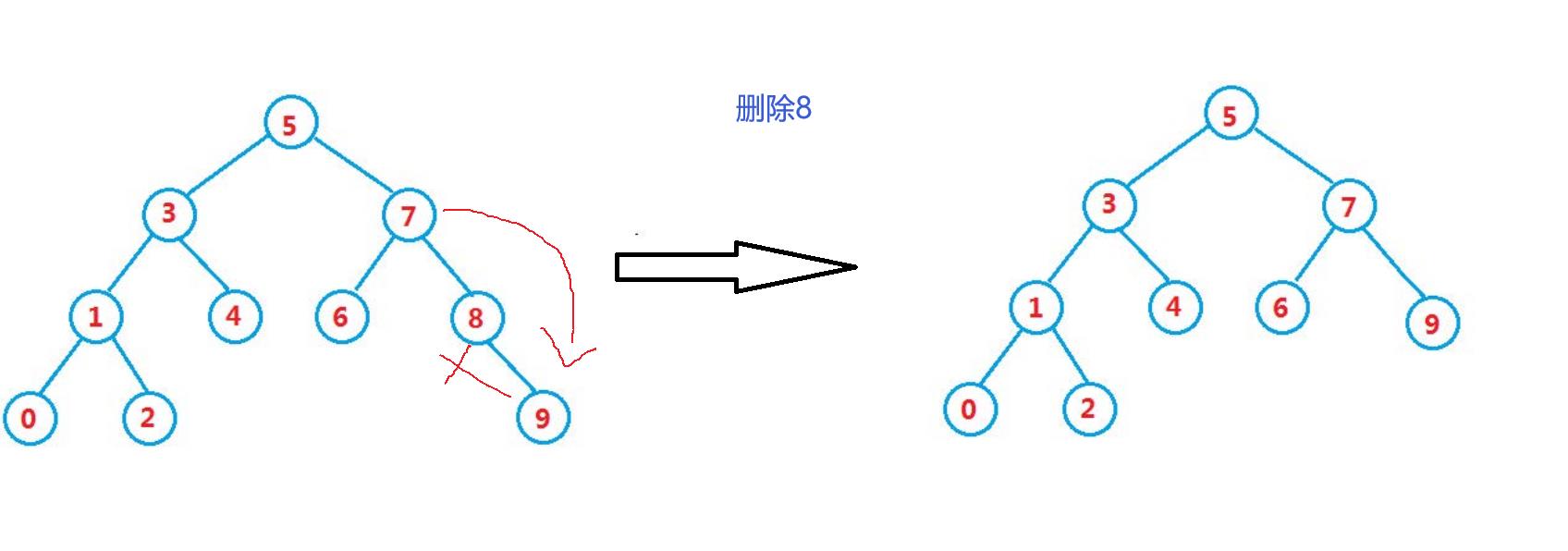
但是这里会存在一个非常极端的情况，那么就是删除的是根节点，这样的话只能让根节点的右孩子结点直接作为根节点

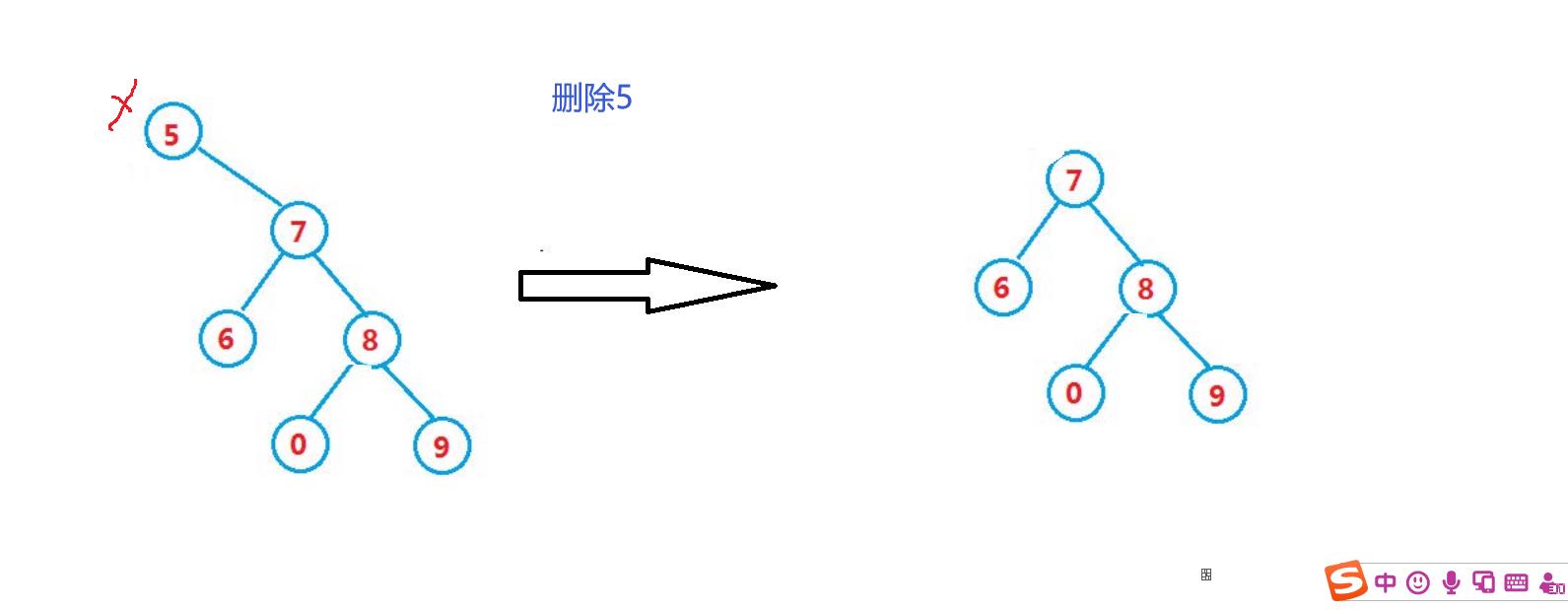
2：如果右为空，那么让父亲的左或者右指向我的左，逻辑和上面相反，这里就不解释了

3：如果左右子树都不空，情况就比较棘手了，我们可以使用移花接木的方法进行删除

• 移花接木：从要删除的结点位置开始，寻找左子树的最右结点（也就是左子树的最大结点）或右子树的最左结点（也就是右子树的最小节点）替代要删除的结点，最终就转化为了删除左为空或右为空的结点了

如下，以寻找右子树的最左结点为例，这里删除根节点5。首先寻找5的右子树的最左结点，是6，用submin标记，同时记录6的父亲结点7，用submin_pre标记；然后将submin处的6直接赋值给要删除的结点5，这样结点5等于就删除了，接着只需要即将submin删除即可。在这种情况下找到的submin一定满足左子树为空，所以符合上面的那种情况，删除后让其父亲结点的左子树或右子树连接到它的右子树11即可

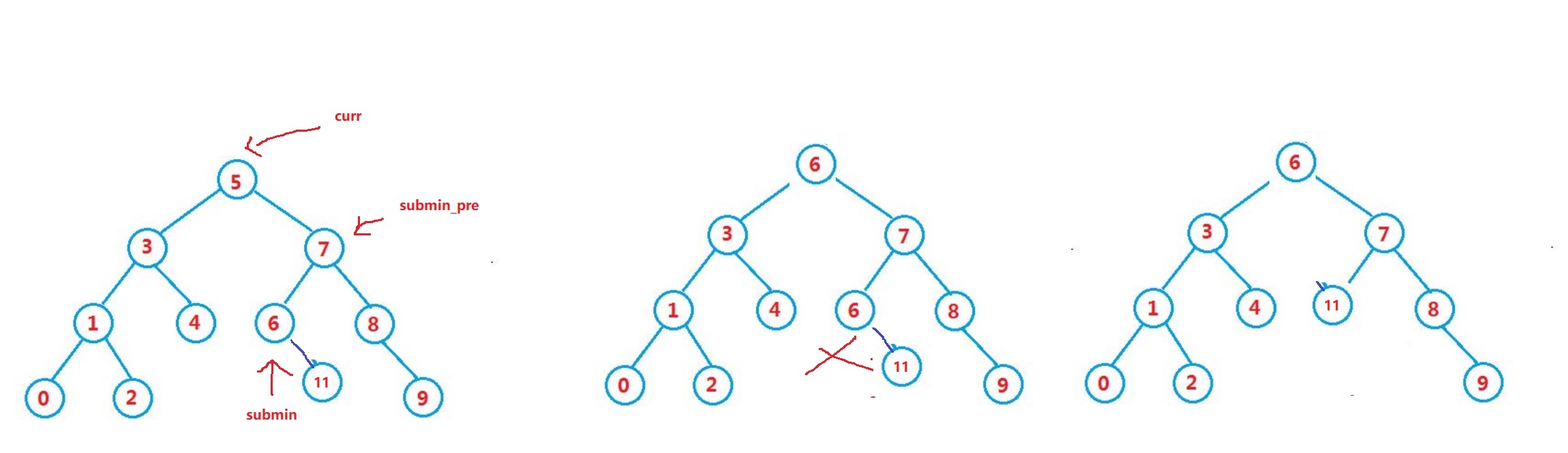
但是要注意一个特殊情况，就是要submin本身就是要删除结点cur右子树的最小结点，所以submin_pre在赋值时，一定要赋值为cur

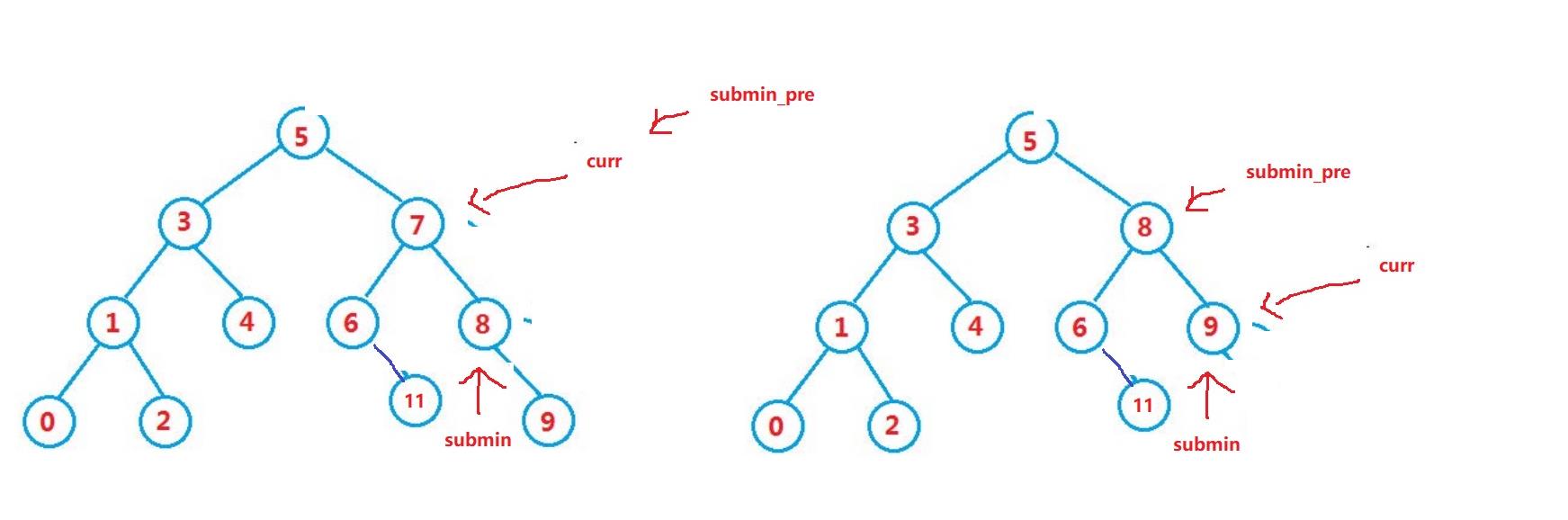
代码如下

bool Erase(const K& key)//二叉搜索树删除
{
	Node* pre = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (key > cur->_key)
		{
			pre = cur;
			cur = cur->_right;
		}
		else if (key < cur->_key)
		{
			pre = cur;
			cur = cur->_left;
		}
		else//找到，开始删除
		{
			//情况1：左子树为空
			if (cur->_left == nullptr)
			{
				if (cur == _root)//如果要删除的结点是根节点
				{
					_root = cur->_right;//让根节点的右节点直接作为根节点
					delete cur;
				}
				else
				{
					if (pre->_left == cur)//如果父亲左不空
					{
						pre->_left = cur->_right;//父亲的左指向我的右
					}
					else//如果父亲的右不空
					{
						pre->_right = cur->_right;//父亲的右指向我的右面
					}
				}
			}
			//情况2：右子树为空
			else if (cur->_right == nullptr)
			{
				if (cur == _root)
				{
					_root = cur->_left;
					delete cur;
				}
				else
				{
					if (pre->_left == cur)
					{
						pre->_left = cur->_left;
					}
					else
					{
						pre->_right = cur->_left;
					}
				}
			}
			//情况3：左右都不为空
			else
			{
				Node* submin_pre = cur;
				Node* submin = cur->_right;
				while (submin->_left)//找寻要删除结点的右子树的最小节点
				{
					submin_pre = submin;
					submin = submin->_left;
				}

				//移花接木
				cur->_key = submin->_key;
				//这种找法下，submin的左子树一定为空,所以删除
				if (submin_pre->_left == submin)
				{
					submin_pre->_left = submin->_right;
				}
				else
				{
					submin_pre->_right = submin->_right;
				}
				delete submin;
			}
			return true;
		}
	}
	return false;

}

测试如下

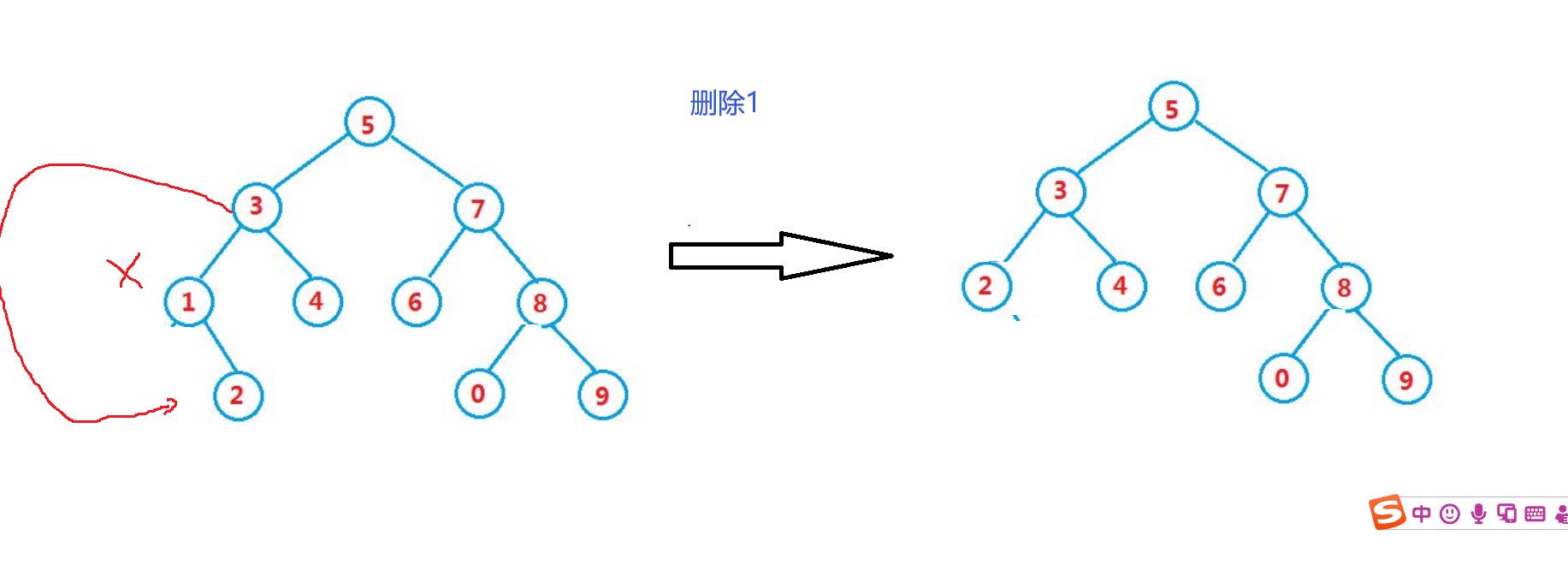
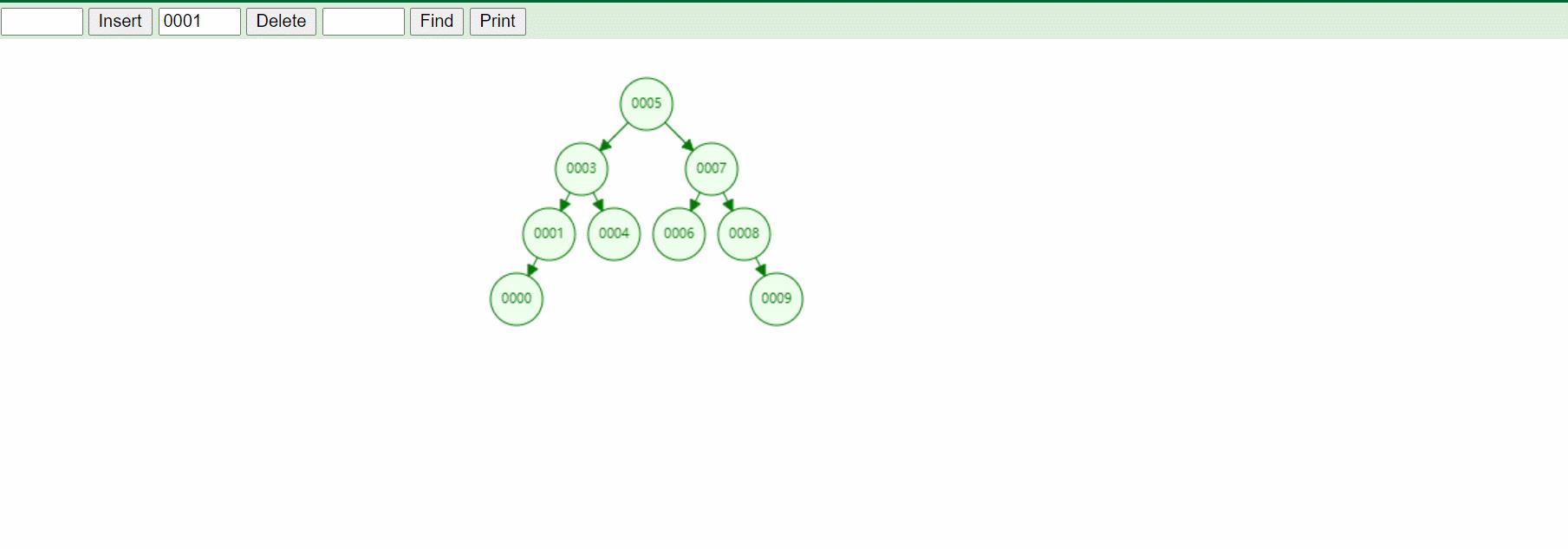
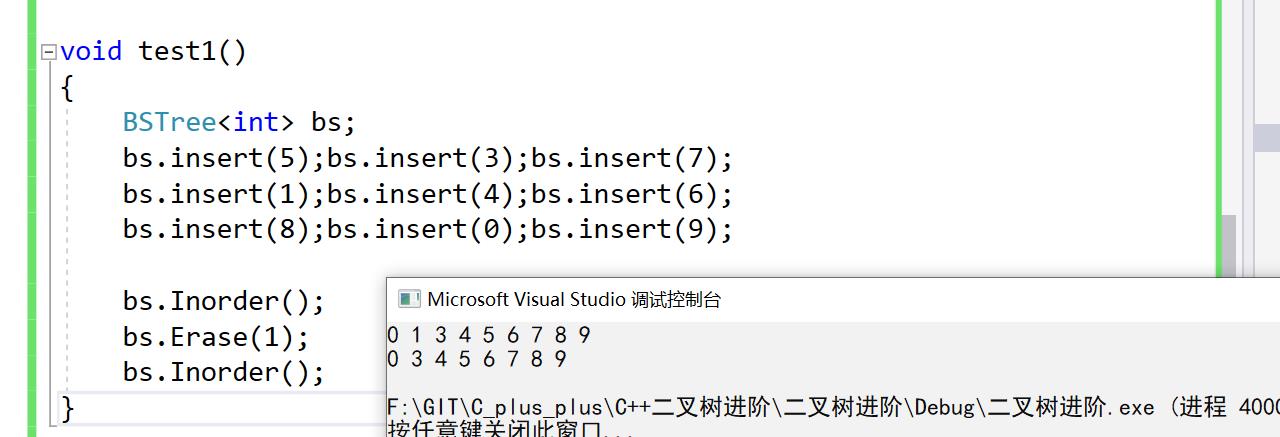
1：删除结点1（右子树空）

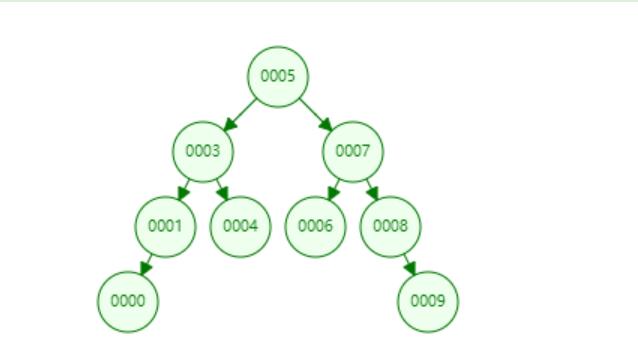
void test1()
{
	BSTree<int> bs;
	bs.insert(5);bs.insert(3);bs.insert(7);
	bs.insert(1);bs.insert(4);bs.insert(6);
	bs.insert(8);bs.insert(0);bs.insert(9);

	bs.Inorder();
	bs.Erase(1);
	bs.Inorder();
}

2:删除节点5，特殊情况下的左子树为空


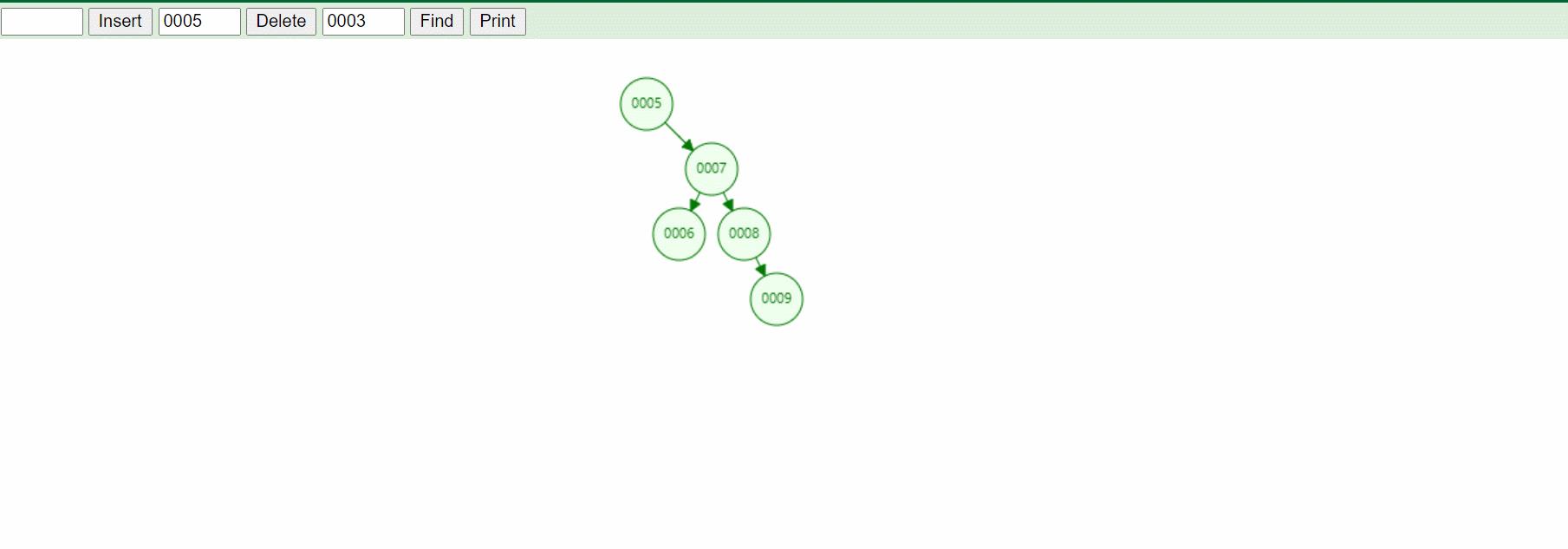
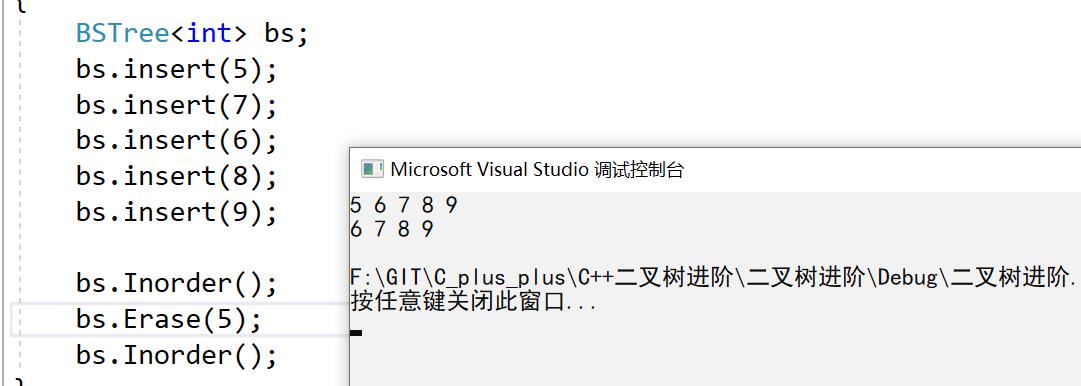
3：删除节点5，特殊情况下的右子树为空

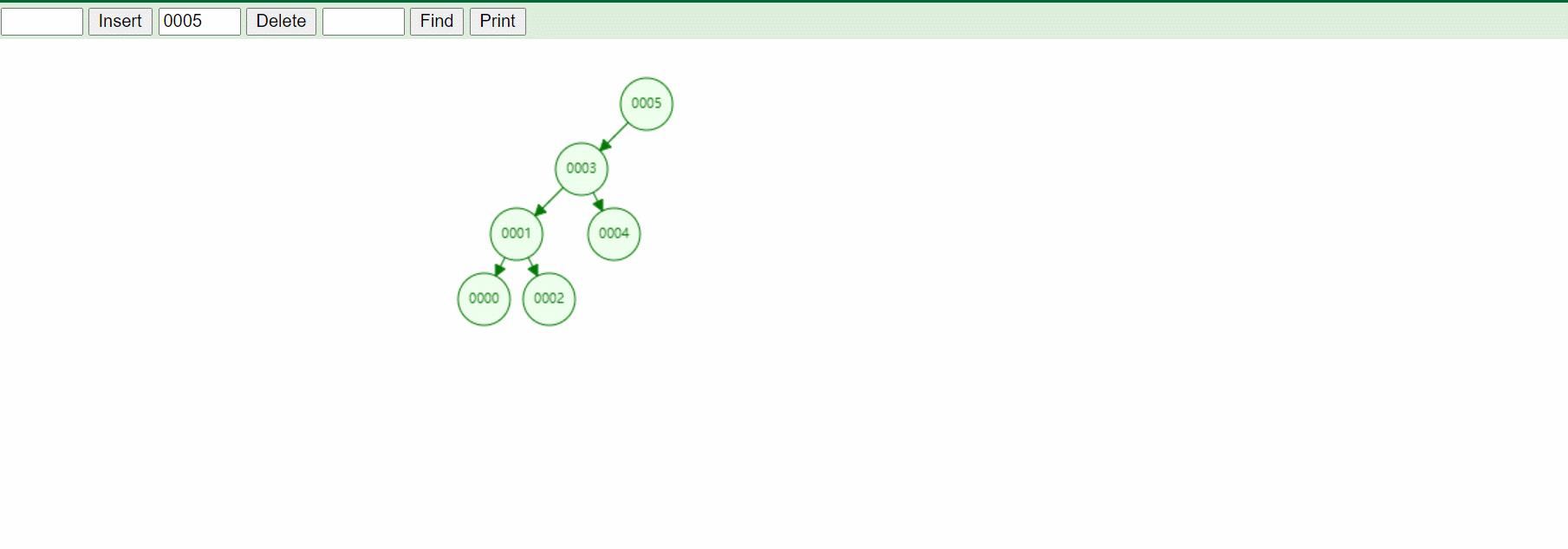
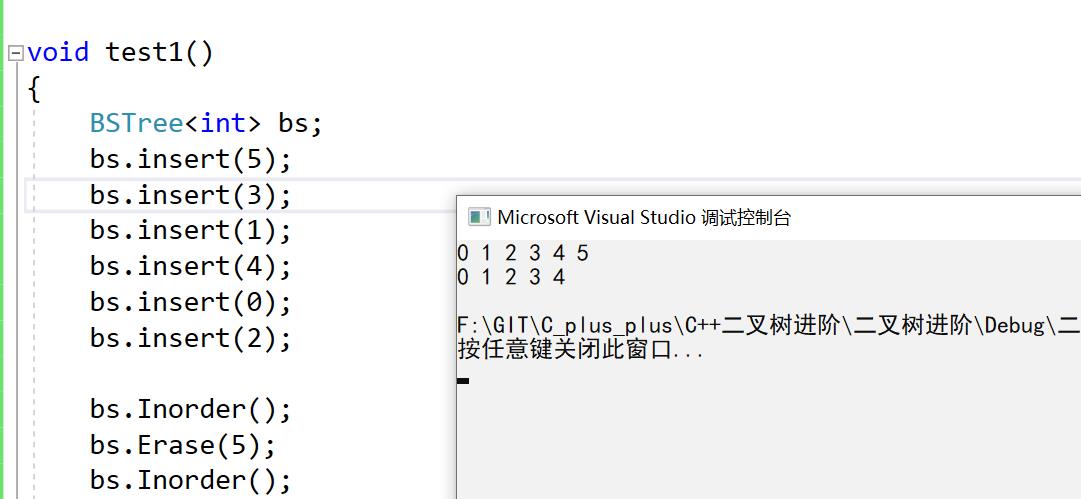
4：删除节点7，属于结点左右子树都存在的情况，其要删除的结点的右子树已经是最小结点的情况


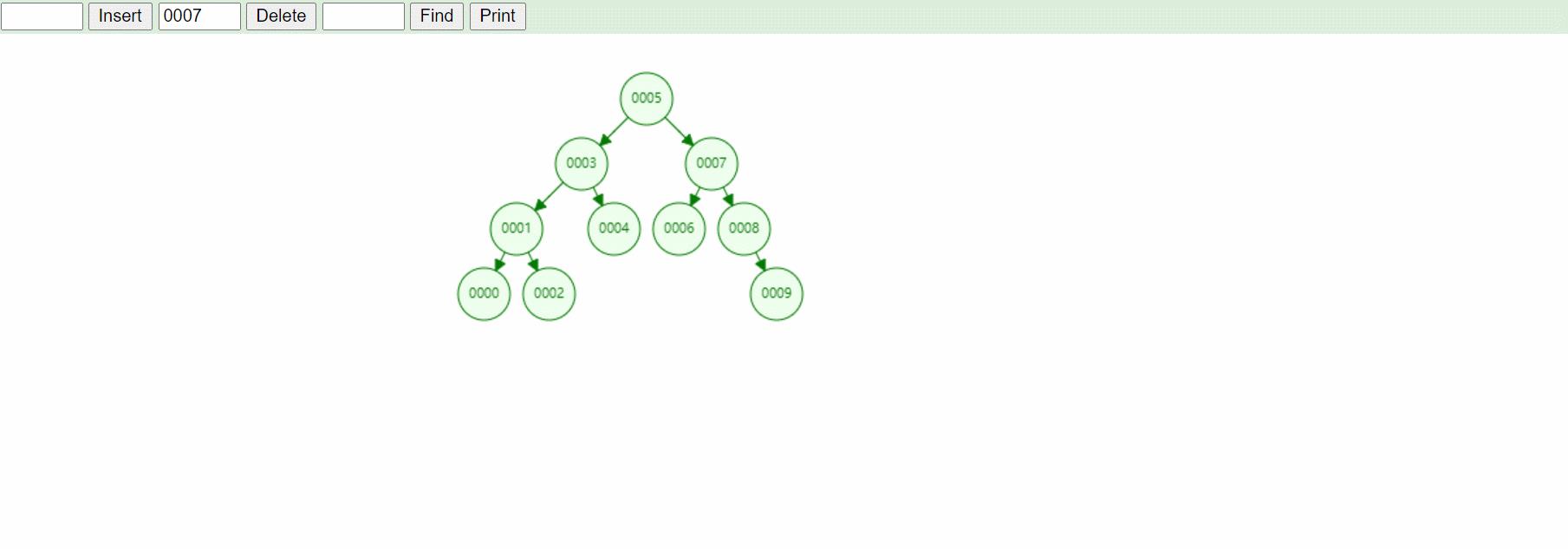
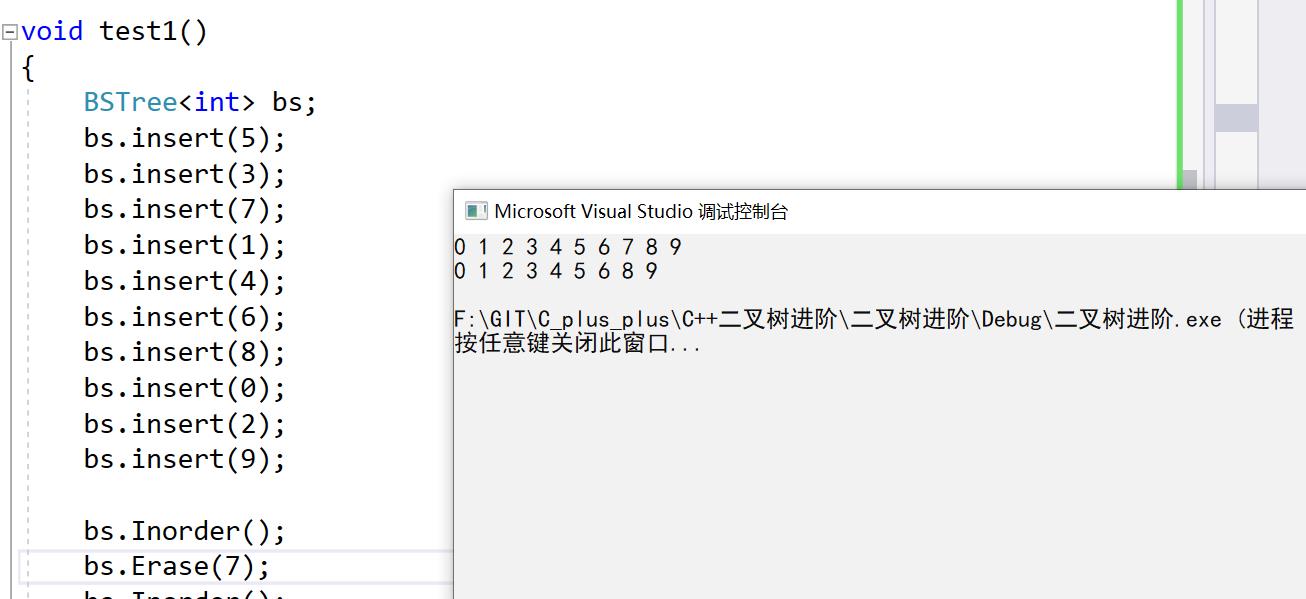
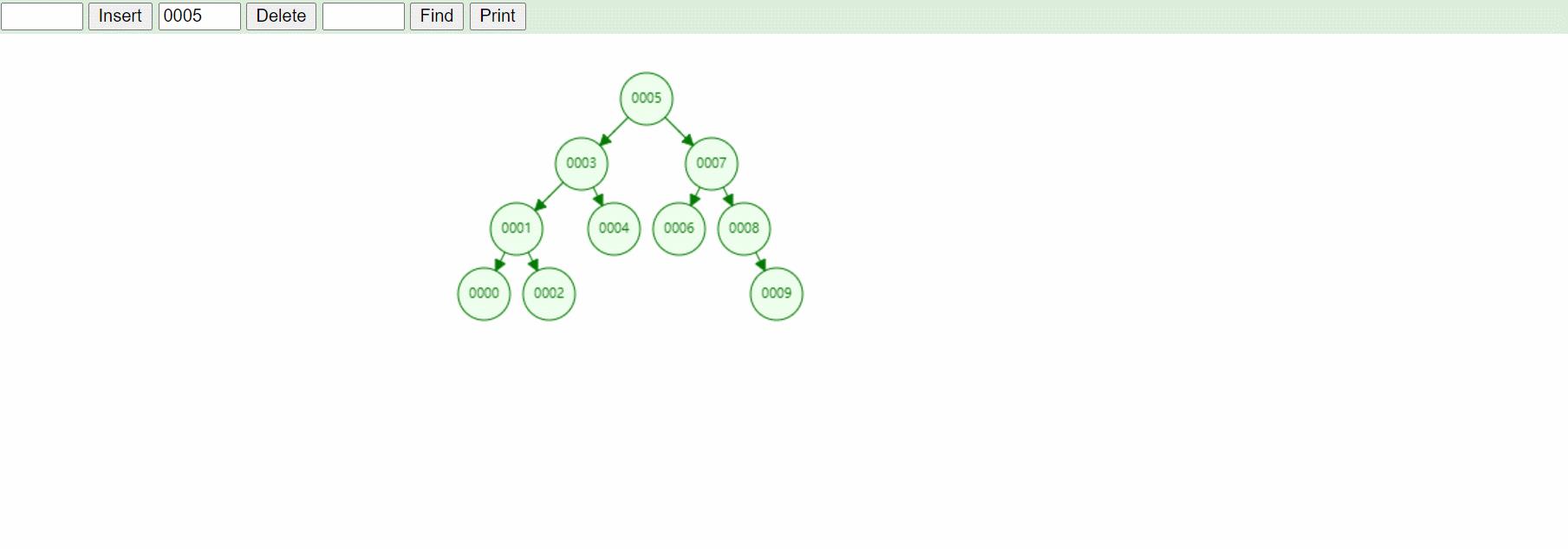
5：删除结点5，正常情况

三：二叉搜索树的应用

1：K模型

K模型以key作为关键码，结构中只需要存储key即可，关键码即为需要搜索的值。比如给定一个单词word判断该单词是否拼写正确，具体方式如下

• 以单词集合中的每个单词作为key，构建一颗二叉搜索树
• 在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则错误

2：KV模型

每一个关键码key，都有一个值value与之对应，也即<key,value>的键值对。比如经典的英文和中文的对应关系，通过因为可以快速的找到与其对应的中文，因为单词与其对应的中文<apple,苹果>就构成了一种键值对。