第十五章15.1矩阵奇异值分解步骤
Posted oldmao_2001
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第十五章15.1矩阵奇异值分解步骤相关的知识,希望对你有一定的参考价值。
本课程来自深度之眼,部分截图来自课程视频以及李航老师的《统计学习方法》第二版。
公式输入请参考: 在线Latex公式
本章内容
任务简介:学习矩阵奇异值分解的定义与基本定理,理解奇异值分解的紧凑和截断形式、几何解释、主要性质,掌握奇异值分解的主要步骤。
本章讲了矩阵奇异值分解的基本原理与实现过程。通过学习第1节,理解奇异值分解的定义与性质,掌握奇异值分解基本定理;通过学习第2节,掌握奇异值分解的计算-5步法;第3节描述奇异值分解与矩阵近似的关系,引入弗罗贝尼乌斯范数,矩阵的最优近似和外积展开式。
学习目标:
1.掌握矩阵奇异值分解法原理。
2.理解奇异值分解的两种形式:紧奇异值分解和截断奇异值分解。
3.理解矩阵奇异值分解与的特征值、特征向量的关系。
4.掌握矩阵奇异值分解步骤与几何意义。
5.理解矩阵的弗罗贝尼乌斯范数定义与性质。
矩阵的奇异值分解
SVD可以很容易得到任意矩阵的满秩分
解,⽤满秩分解可以对数据做压缩。
可以⽤SVD来证明对任意
M
×
N
M\\times N
M×N的矩阵
均存在如下图的分解:
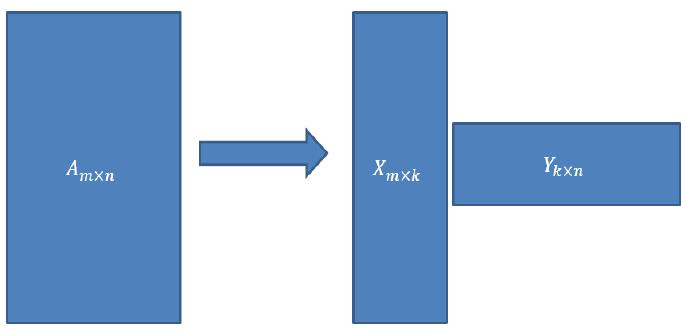
其中
k
=
r
a
n
k
(
A
)
k=rank(A)
k=rank(A)
这个经常用来数据降维,例如有m个样本,每个样本的维度是n,如果要降维至r维,那么就将m×n矩阵乘以一个n×r的矩阵,就得到m×r的矩阵,达到降维的目的。
注意降维是特征筛选的一种。
正交矩阵
正交矩阵是在欧⼏⾥得空间⾥的名称,在⾣空间⾥被称为⾣矩阵。
⼀个正交矩阵对应的变换叫正交变换,这个变换的特点是不改变向量的尺⼨和向量间的夹⻆。
正交变换是将变换向量⽤另⼀组正交基表示,在这个过程中并没有对向量做拉伸,也不改变向量的空间位置。(可以看成改变是坐标系)
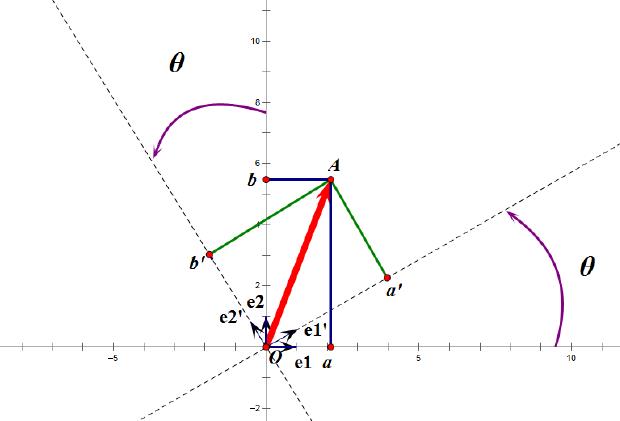
在新坐标系下向量的投影当然是有旋转和变化的。
如果选择
e
1
′
e1'
e1′、
e
2
′
e2'
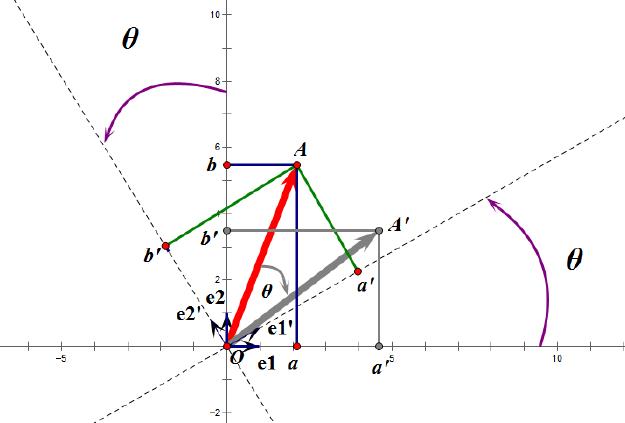
e2′作为新的标准坐标系,那么在新坐标系中OA(原标准坐标系的表示)变成OA’,看起来像坐标系不动,把OA往顺时针⽅向旋转了θ⻆度。
正交矩阵的⾏(列)向量都是两两正交的单位向量,正交矩阵对应的变换为正交变换,它有两种表现:旋转和反射。
正交矩阵将标准正交基映射为标准正交基(即上图中从
e
1
e1
e1、
e
2
e2
e2到
e
1
′
e1'
e1′、
e
2
′
e2'
e2′)
矩阵的奇异值分解
现在假设存在M*N矩阵A,事实上,A矩阵将n维空间中的向量映射到k(k<=m)维空间中,k=Rank(A)。
现在的目标是:在n维空间中找一组正交基,使得经过A变换后还是正交的。假设已经找到这样一组正交基:
{
v
1
,
v
2
…
,
v
n
}
\\{v_1,v_2…,v_n\\}
{v1,v2…,vn}
则A将这组基映射为:
{
A
v
1
,
A
v
2
,
…
,
A
v
n
}
\\{Av_1,Av_2,…,Av_n\\}
{Av1,Av2,…,Avn}
现在假设存在两组相互正交的基,且其模长为1:
v
i
T
v
j
=
v
i
⋅
v
j
=
0
v_i^Tvj=v_i\\cdot v_j=0
viTvj=vi⋅vj=0
所以如果正交基
v
v
v选择为
A
T
A
A^TA
ATA的特征向量的话,由于
A
T
A
A^TA
ATA是对称阵,
v
v
v之间两两正交,那么这样就找到了正交基使其映射后还是正交基了,现在,将映射后的正交基单位化。因为
A
v
i
⋅
A
v
i
=
λ
i
v
i
⋅
v
i
=
λ
i
Av_i\\cdot Av_i=\\lambda_iv_i\\cdot v_i=\\lambda_i
Avi⋅Avi=λivi⋅vi=λi
所以有
∣
A
v
i
∣
2
=
λ
i
≥
0
|Av_i|^2=\\lambda_i\\ge0
∣Avi∣2=λi≥0
上面的内容感觉老师讲的和ppt内容相差太远。。。
摘录一点板书内容
如果矩阵
A
m
×
n
A_{m\\times n}
Am×n的秩
r
a
n
k
(
A
)
=
k
≤
min
(
m
,
n
)
rank(A)=k\\le \\min(m,n)
rank(A)=k≤min(m,n),那么
A
T
A
A^TA
ATA或者
A
A
T
AA^T
AAT的秩也是k
证明:
假设矩阵方程
A
X
=
0
AX=0
AX=0成立
等式两边同时乘以一个东西也成立:
A
T
A
X
=
0
A^TAX=0
ATAX=0
也就是说X是两个矩阵方程的解,也就是说上面方程的解空间属于下面方程的解空间。
也就是上面方程的解空间维度(
n
−
r
a
n
k
(
A
)
n-rank(A)
n−rank(A))小于下面方程的解空间的维度(
n
−
r
a
n
k
(
A
T
A
)
n-rank(A^TA)
n−rank(ATA))。
n
−
r
a
n
k
(
A
)
≤
n
−
r
a
n
k
(
A
T
A
)
−
r
a
n
k
(
A
)
≤
−
r
a
n
k
(
A
T
A
)
r
a
n
k
(
A
)
≥
r
a
n
k
(
A
T
A
)
n-rank(A)\\le n-rank(A^TA)\\\\ -rank(A)\\le -rank(A^TA)\\\\ rank(A)\\ge rank(A^TA)
n−rank(A)≤n−rank(ATA)−rank(A)≤−rank(ATA)rank(A)≥rank(ATA)
上面的方程
A
T
A
X
=
0
A^TAX=0
ATAX=0再左右乘以一个东西还是成立的:
X
T
A
T
A
X
=
0
=
∣
∣
A
X
∣
∣
2
X^TA^TAX=0=||AX||^2
XTATAX=0=∣∣AX∣∣2
也就是
A
X
=
0
AX=0
AX=0,从这个推导我们可以得出结论
r
a
n
k
(
A
)
=
r
a
n
k
(
A
T
A
)
=
r
a
n
k
(
A
A
T
)
=
rank(A)= rank(A^TA)=rank(AA^T)=
rank(A)=rank(ATA)=rank(AAT)=
接上面,由于
A
T
A
,
A
A
T
A^TA,AA^T
ATA,AAT都是半正定矩阵,因此有k个特征向量,写为: 以上是关于第十五章15.1矩阵奇异值分解步骤的主要内容,如果未能解决你的问题,请参考以下文章
λ
1
2
≥
λ
2
2
≥
⋯
≥
λ
k
2
\\lambda^2_1\\ge\\lambda^2_2\\ge\\cdots\\ge\\lambda^2_k
λ12≥λ22≥⋯≥λk2
A
v
i
⋅
A
v
i