今天老夫就把完全背包的底裤给你扒出来瞅瞅！！！

Posted 2021-05-23 大忽悠爱忽悠

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了今天老夫就把完全背包的底裤给你扒出来瞅瞅！！！相关的知识，希望对你有一定的参考价值。

来我房里有些好康的，来看看完全背包的底裤

完全背包
双重for循环遍历顺序再探
C++测试代码
总结
最后再啰嗦一下，稍微总结一下完全背包需要的注意事项

完全背包

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

在下面的讲解中，我依然举01背包的底裤里面的这个例子：

背包最大重量为4。

物品为：

在这里插入图片描述
每件商品都有无限个！

问背包能背的物品最大价值是多少？

01背包和完全背包唯一不同就是体现在遍历顺序上，所以本文就不去做动规五部曲了，我们直接针对遍历顺序经行分析！

首先再回顾一下01背包的核心代码:

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

我们知道01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。

而完全背包的物品是可以添加多次的，所以要从小到大去遍历，即：

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j < bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

至于为什么，我在01背包问题中也做了讲解。

这里需要注意j的起点，考虑放入当前物品的前提是当前物品的大小没有超过当前背包容量的大小，对于那些容量小于当前物品大小的状态来说，就维持旧状态即可，等于不选择当前物品

dp状态图如下：
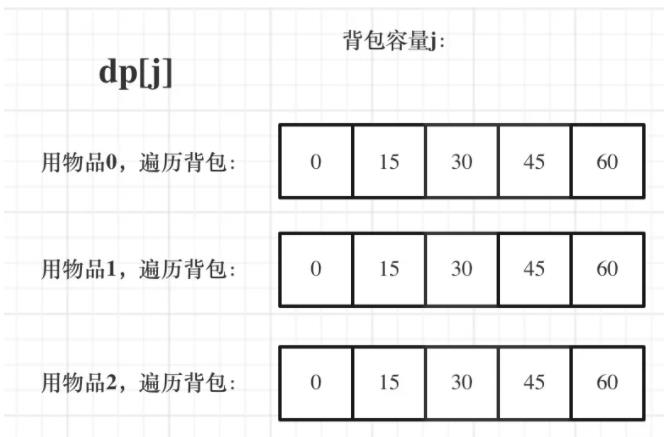
在这里插入图片描述
完全背包先介绍到这，因为之前已经写过关于完全背包的文章了，文章链接放在下面:
LintCode 440 · 背包问题 III—完全背包问题
 leetcode 279. 完全平方数----完全背包的套路
 leetcode 322. 零钱兑换----完全背包套路解法详细再探

双重for循环遍历顺序再探

其实还有一个很重要的问题，为什么遍历物品在外层循环，遍历背包容量在内层循环？

这个问题很多题解关于这里都是轻描淡写就略过了，大家都默认遍历物品在外层，遍历背包容量在内层，好像本应该如此一样，那么为什么呢？

难道就不能遍历背包容量在外层，遍历物品在内层？

看过这篇的话：01背包问题就知道了，01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一位dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。

在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序同样无所谓！，二维不用提更加无所谓

因为dp[j] 是根据下标j之前所对应的dp[j]计算出来的。只要保证下标j之前的dp[j]都是经过计算的就可以了。

遍历物品在外层循环，遍历背包容量在内层循环，状态如图：
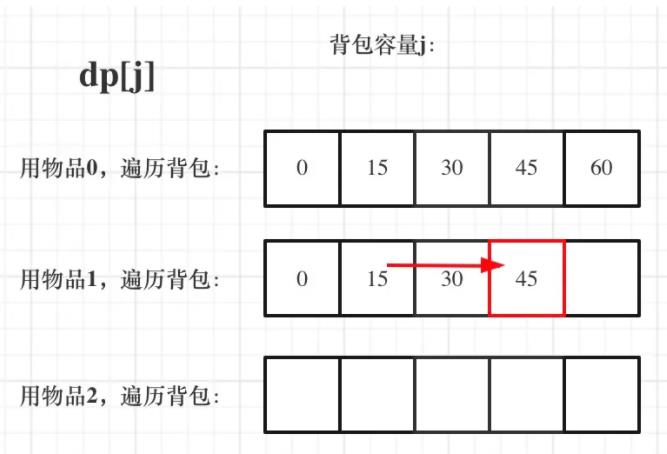
在这里插入图片描述
遍历背包容量在外层循环，遍历物品在内层循环，状态如图：

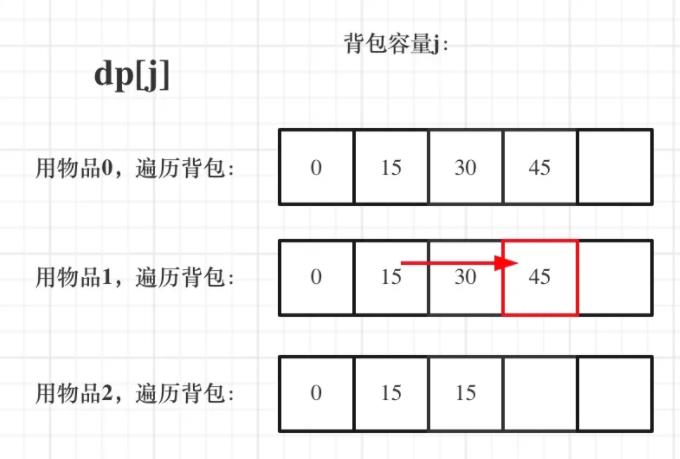
看了这两个图，大家就会理解，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值（这个值就是下标j之前所对应的dp[j]）。

先遍历背包再遍历物品，代码如下：

// 先遍历背包，再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

C++测试代码

题目链接—LintCode 440背包问题|||

1.先遍历物品再遍历背包容量的版本

class Solution {
public:
	int backPackIII(vector<int>& A, vector<int>& V, int m)
	{
		int size = A.size();//物品个数
		vector<int> dp(m + 1, 0);

		for (int i = 0; i < size; i++)
		{
			for (int j =A[i]; j <= m; j++)//注意j起点值，从小到大遍历
			{
				dp[j] = max(dp[j], dp[j - A[i]] + V[i]);
			}
		}
		return dp[m];
	}
};

在这里插入图片描述

2.先遍历背包容量再遍历物品的版本

class Solution {
public:
	int backPackIII(vector<int>& A, vector<int>& V, int m)
	{
		int size = A.size();//物品个数
		vector<int> dp(m + 1, 0);
        
		for (int j = 0; j <= m; j++)
		{
			for (int i = 0; i < size; i++)
			{
				//因为这里把物品遍历放在内侧,因此这里需要做可否放进背包的判断
				if (j >= A[i]) dp[j] = max(dp[j], dp[j - A[i]] + V[i]);
			}
		}
		return dp[m];
	}
};