Leetcode No.44 通配符匹配

Posted 2021-05-22 AI算法攻城狮

一、题目描述

给定一个字符串 (s) 和一个字符模式 (p) ，实现一个支持 '?' 和 '*' 的通配符匹配。

'?' 可以匹配任何单个字符。
'*' 可以匹配任意字符串（包括空字符串）。
两个字符串完全匹配才算匹配成功。

说明:s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 *。

示例 1:
输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

示例 2:
输入:
s = "aa"
p = "*"
输出: true
解释: '*' 可以匹配任意字符串。

示例 3:
输入:
s = "cb"
p = "?a"
输出: false
解释: '?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。

示例 4:
输入:
s = "adceb"
p = "*a*b"
输出: true
解释: 第一个 '*' 可以匹配空字符串, 第二个 '*' 可以匹配字符串 "dce".

示例 5:
输入:
s = "acdcb"
p = "a*c?b"
输出: false

二、解题思路：动态规划

思路与算法

在给定的模式 p 中，只会有三种类型的字符出现：

小写字母 a−z，可以匹配对应的一个小写字母；

问号 ?，可以匹配任意一个小写字母；

星号 *，可以匹配任意字符串，可以为空，也就是匹配零或任意多个小写字母。

其中「小写字母」和「问号」的匹配是确定的，而「星号」的匹配是不确定的，因此我们需要枚举所有的匹配情况。为了减少重复枚举，我们可以使用动态规划来解决本题。

我们用 dp[i][j] 表示字符串 s 的前 i 个字符和模式 p 的前 j 个字符是否能匹配。在进行状态转移时，我们可以考虑模式 p 的第 j个字符 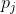 ，与之对应的是字符串 s 中的第 i个字符 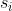,如果 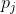是小写字母，那么 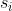必须也为相同的小写字母，状态转移方程为：
dp[i][j]=(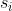与 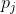相同)∧dp[i−1][j−1]

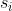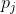其中 ∧ 表示逻辑与运算。也就是说，dp[i][j] 为真，当且仅当dp[i−1][j−1] 为真，并且 与相同。

如果 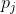是问号，那么对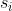没有任何要求，状态转移方程为：
dp[i][j]=dp[i−1][j−1]

如果 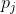是星号，那么同样对 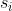没有任何要求，但是星号可以匹配零或任意多个小写字母，因此状态转移方程分为两种情况，即使用或不使用这个星号：
dp[i][j]=dp[i][j−1]∨dp[i−1][j]

其中∨ 表示逻辑或运算。如果我们不使用这个星号，那么就会从 dp[i][j−1] 转移而来；如果我们使用这个星号，那么就会从dp[i−1][j] 转移而来。

最终的状态转移方程如下：

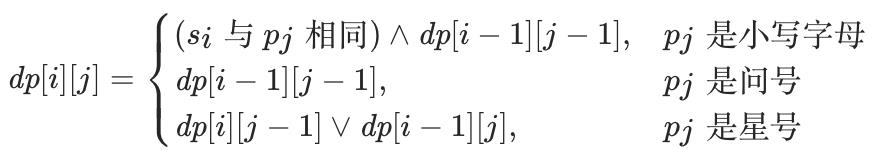
我们也可以将前两种转移进行归纳：

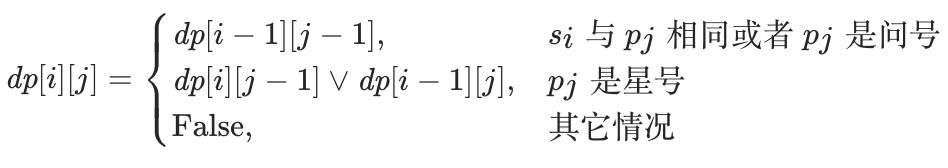
细节

只有确定了边界条件，才能进行动态规划。在上述的状态转移方程中，由于 dp[i][j] 对应着 s 的前 i 个字符和模式 p 的前 j 个字符，因此所有的 dp[0][j] 和dp[i][0] 都是边界条件，因为它们涉及到空字符串或者空模式的情况，这是我们在状态转移方程中没有考虑到的：

dp[0][0]=True，即当字符串 s 和模式 p 均为空时，匹配成功；

dp[i][0]=False，即空模式无法匹配非空字符串；

dp[0][j] 需要分情况讨论：因为星号才能匹配空字符串，所以只有当模式 p 的前 j 个字符均为星号时，dp[0][j] 才为真。

我们可以发现，dp[i][0] 的值恒为假，dp[0][j] 在 j 大于模式 p 的开头出现的星号字符个数之后，值也恒为假，而dp[i][j] 的默认值（其它情况）也为假，因此在对动态规划的数组初始化时，我们就可以将所有的状态初始化为False，减少状态转移的代码编写难度。

最终的答案即为 dp[m][n]，其中 m 和 n 分别是字符串 s 和模式 p 的长度。需要注意的是，由于大部分语言中字符串的下标从 0 开始，因此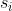 和 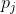分别对应着 s[i-1] 和p[j−1]。

三、代码

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size();
        int n = p.size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        dp[0][0] = true;
        for (int i = 1; i <= n; ++i) {
            if (p[i - 1] == '*') {
                dp[0][i] = true;
            }
            else {
                break;
            }
        }
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (p[j - 1] == '*') {
                    dp[i][j] = dp[i][j - 1] | dp[i - 1][j];
                }
                else if (p[j - 1] == '?' || s[i - 1] == p[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                }
            }
        }
        return dp[m][n];
    }
};

四、复杂度分析

时间复杂度：O(mn)，其中 m 和 n 分别是字符串 s 和模式 p 的长度。

空间复杂度：O(mn)，即为存储所有(m+1)(n+1) 个状态需要的空间。此外，在状态转移方程中，由于dp[i][j] 只会从 dp[i][..] 以及dp[i−1][..] 转移而来，因此我们可以使用滚动数组对空间进行优化，即用两个长度为 n+1 的一维数组代替整个二维数组进行状态转移，空间复杂度为 O(n)。