HDU2815 Mod Tree大步小步法

Posted 2021-05-22 海岛Blog

Mod Tree
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 8555 Accepted Submission(s): 1992

Problem Description

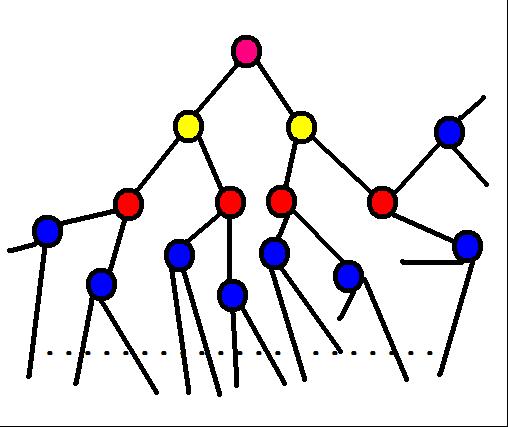
The picture indicates a tree, every node has 2 children.
The depth of the nodes whose color is blue is 3; the depth of the node whose color is pink is 0.
Now out problem is so easy, give you a tree that every nodes have K children, you are expected to calculate the minimize depth D so that the number of nodes whose depth is D equals to N after mod P.

Input
The input consists of several test cases.
Every cases have only three integers indicating K, P, N. (1<=K, P, N<=10^9)

Output
The minimize D.
If you can’t find such D, just output “Orz,I can’t find D!”

Sample Input
3 78992 453
4 1314520 65536
5 1234 67

Sample Output
Orz,I can’t find D!
8
20

Author
AekdyCoin

Source
HDU 1st “Old-Vegetable-Birds Cup” Programming Open Contest

问题链接：HDU2815 Mod Tree
问题简述：（略）
问题分析：用扩展大步小步法来解决，不解释。
程序说明：（略）
参考链接：（略）
题记：（略）

AC的C++语言程序如下：

/* HDU2815 Mod Tree */

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

// 快速模幂
LL qpow(LL x, LL n, LL m)
{
    LL ret = 1;
    while (n) {
        if (n & 1) ret = ret * x % m;
        x = x * x % m;
        n >>= 1;
    }
    return ret;
}

LL exBSGS(LL a, LL b, LL n)
{
    a %= n, b %= n;
    if (b == 1) return 0;

    LL cnt = 0, d = 1, t = __gcd(a, n);
    while (t != 1) {
        if (b % t) return -1;
        b /= t;
        n /= t;
        cnt++;
        d = d * (a / t) % n;
        if (b == d) return cnt;
        t = __gcd(a, n);
    }

    map<int, LL> mp;
    int m = sqrt(n);
    LL ans = b;
    t = qpow(a, m, n);
    mp[ans] = 0;
    for (int i = 1; i <= m; i++)
        ans = ans * a % n, mp[ans] = i;
    for (int i = 1; i <= m + 1; i++) {
        d = d * t % n;
        if (mp[d]) return i * m - mp[d] + cnt;
    }

    return -1;
}

int main()
{
    LL k, p, n, ans;
    while (~scanf("%lld%lld%lld", &k, &p, &n)) {
        if (n >= p) printf("Orz,I can’t find D!\\n");
        else {
            if ((ans = exBSGS(k, n, p)) == -1)
                printf("Orz,I can’t find D!\\n");
            else
                printf("%lld\\n", ans);
        }
    }

    return 0;
}