HDU 2815 Mod Tree

Posted 2020-10-23 Z-Y-Y-S

Problem Description

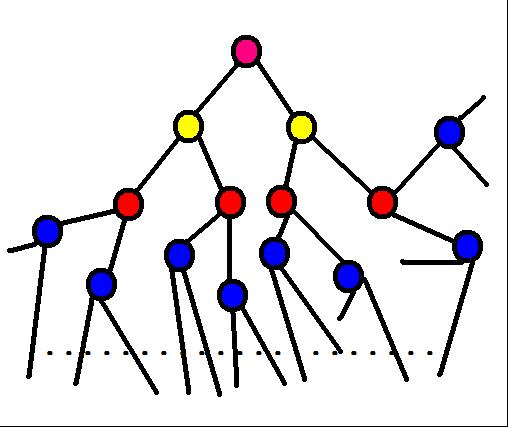
  The picture indicates a tree, every node has 2 children.
  The depth of the nodes whose color is blue is 3; the depth of the node whose color is pink is 0.
  Now out problem is so easy, give you a tree that every nodes have K children, you are expected to calculate the minimize depth D so that the number of nodes whose depth is D equals to N after mod P.

Input

The input consists of several test cases.
Every cases have only three integers indicating K, P, N. (1<=K, P, N<=10^9)

Output

The minimize D.
If you can’t find such D, just output “Orz,I can’t find D!”

Sample Input

3 78992 453

4 1314520 65536

5 1234 67

 

Sample Output

Orz,I can’t find D!

8

20

大意：一个k叉数，求小深度D，使得叶子节点数模P为N

即求解k^D≡N (mod P)

拓展BSGS

注意N不能大于等于P

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<algorithm>
  5 #include<cmath>
  6 using namespace std;
  7 typedef long long lol;
  8 int MOD=250000;
  9 lol ha[300001],id[300001];
 10 void insert(lol x,lol d)
 11 {
 12   lol pos=x%MOD;
 13   while (1)
 14     {
 15       if (ha[pos]==-1||ha[pos]==x)
 16     {
 17       ha[pos]=x;
 18       id[pos]=d;
 19       return;
 20     }
 21       pos++;
 22       if (pos>=MOD) pos-=MOD;
 23     }
 24 }
 25 bool count(lol x)
 26 {
 27   lol pos=x%MOD;
 28   while (1)
 29     {
 30       if (ha[pos]==-1) return 0;
 31       if (ha[pos]==x) return 1;
 32       pos++;
 33       if (pos>=MOD) pos-=MOD;
 34     }
 35 }
 36 lol query(lol x)
 37 {
 38   lol pos=x%MOD;
 39   while (1)
 40     {
 41       if (ha[pos]==x) return id[pos];
 42       pos++;
 43       if (pos>=MOD) pos-=MOD;
 44     }
 45 }
 46 lol qpow(lol x,lol y,lol Mod)
 47 {
 48   lol res=1;
 49   while (y)
 50     {
 51       if (y&1) res=res*x%Mod;
 52       x=x*x%Mod;
 53       y>>=1;
 54     }
 55   return res;
 56 }
 57 lol gcd(lol a,lol b)
 58 {
 59   if (!b) return a;
 60   return gcd(b,a%b);
 61 }
 62 lol BSGS(lol a,lol b,lol Mod)
 63 {lol i;
 64   if (b==1) return 0;
 65   if (a==0&&b!=0) return -1;
 66   if (b>=Mod) return -1;
 67   memset(ha,-1,sizeof(ha));
 68   memset(id,0,sizeof(id));
 69   lol cnt=0,d=1,t;
 70   while ((t=gcd(a,Mod))!=1)
 71     {
 72       if (b%t) return -1;
 73       cnt++;
 74       b/=t;Mod/=t;
 75       d=d*(a/t)%Mod;
 76       if (d==b) return cnt;
 77     }
 78   lol tim=sqrt((double)Mod);
 79   lol tmp=b%Mod;
 80   for (i=0;i<=tim;i++)
 81     {
 82       insert(tmp,i);
 83       tmp=tmp*a%Mod;
 84     }
 85   t=tmp=qpow(a,tim,Mod);
 86   tmp=tmp*d%Mod;
 87   for (i=1;i<=tim;i++)
 88     {
 89       if (count(tmp))
 90     return i*tim-query(tmp)+cnt;
 91       tmp=tmp*t%Mod;
 92     }
 93   return -1;
 94 }
 95 int main()
 96 {lol a,b,Mod,ans;
 97   while (cin>>a>>Mod>>b)
 98     {
 99       ans=BSGS(a,b,Mod);
100       if (ans==-1) printf("Orz,I can’t find D!\n");
101       else printf("%lld\n",ans);
102     }
103 }