开发成长之路（16）-- 算法小抄：思维跃迁

Posted 2021-05-22 看，未来

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了开发成长之路（16）-- 算法小抄：思维跃迁相关的知识，希望对你有一定的参考价值。

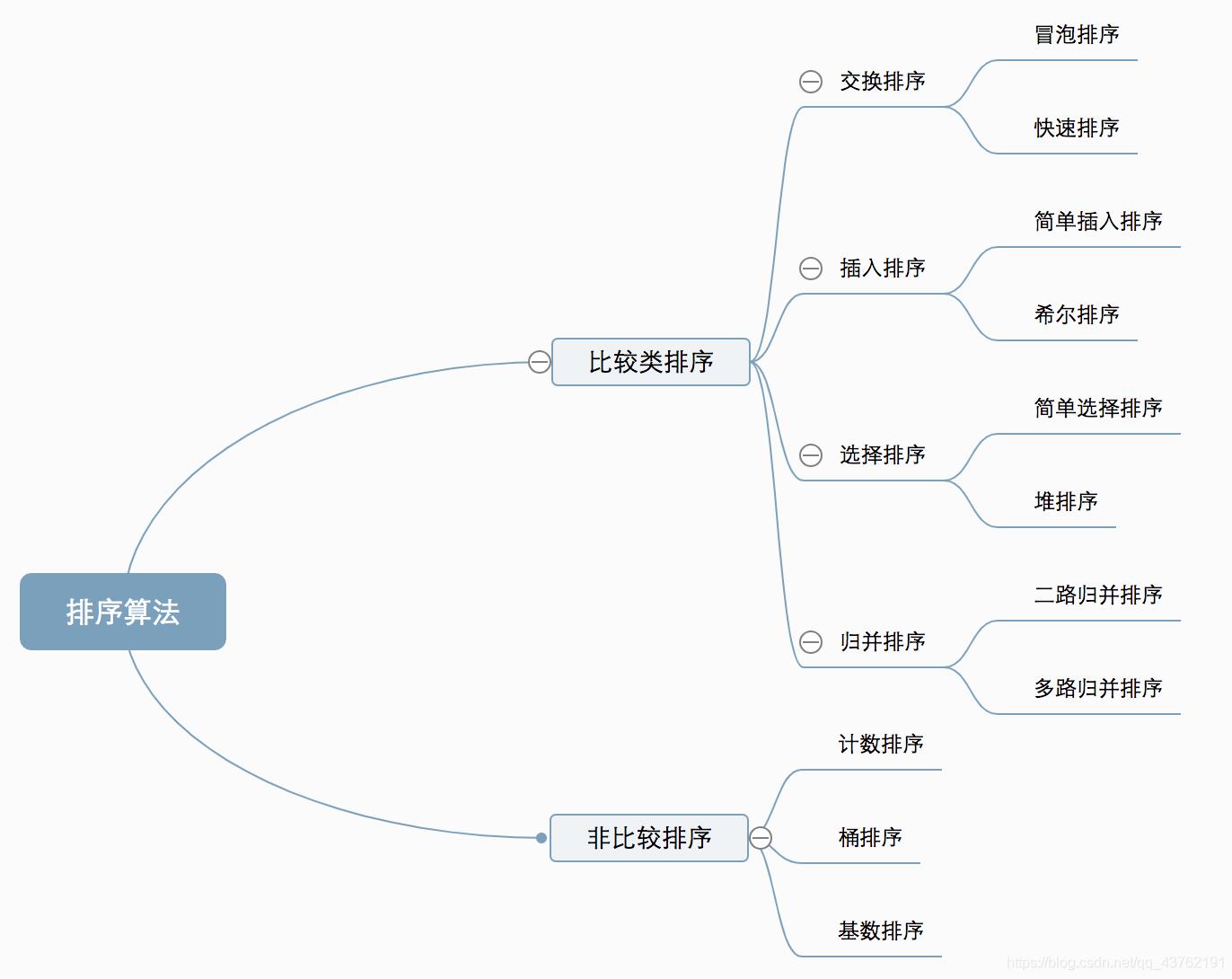
在这里插入图片描述

文章目录

排序算法

在这里插入图片描述

冒泡排序：
在这里插入图片描述

复杂度分析：
在一般情况下，每一个数都要与之后的数进行匹配，所以匹配次数将与数据量n挂钩，又由于每轮匹配都要进行(n-1)次比较，所以平均时间复杂度为O(n^2)。

当然，可以对冒泡排序进行优化，比方说可以设置一个标志位，当哪次匹配没有发生数据交换时，就不用再进行后面的匹配了。
还可以做个优化，纪录下数据尾部已经稳定下的部分，比如说倒数八个数字已经稳定，那么匹配到倒数第九个数，只要和倒八匹配一下即可知道要不要往后继续匹配。

不过，冒泡排序一般也不会用在大数排序上，所以嘛，老老实实的把基础代码写好比较重要。

快速排序：
在这里插入图片描述

快速排序是很重要的算法，和傅里叶变化等算法并称二十世纪最伟大的十大算法。

快速排序的核心思维就是“分而治之”，就像封建王朝的“分封制”。将一大块“领土”，依据“嫡庶长幼”，分为不同部分，各个部分在自行细分，直到分无可分之后，便等级森严了。

说白点，就是在序列中找个元素充当中间量，大的往后，小的往前，一分为二，二分为四，四分为八···

那么，快速排序的技术核心，便呼之欲出了。其一就是这个中间量怎么找，其二就是怎么移动各个元素。

······
此外，插入、希尔、堆排、选排、归并等一系列排序方法尽在：【C++】算法集锦（1）：八大排序算法：GIF + 亲测代码 +专项练习平台

递归算法

1、明确你要干嘛
2、明确递归的结束条件
3、寻找递推关系式
4、注意边界条件与调用方式

递归中的记忆化：
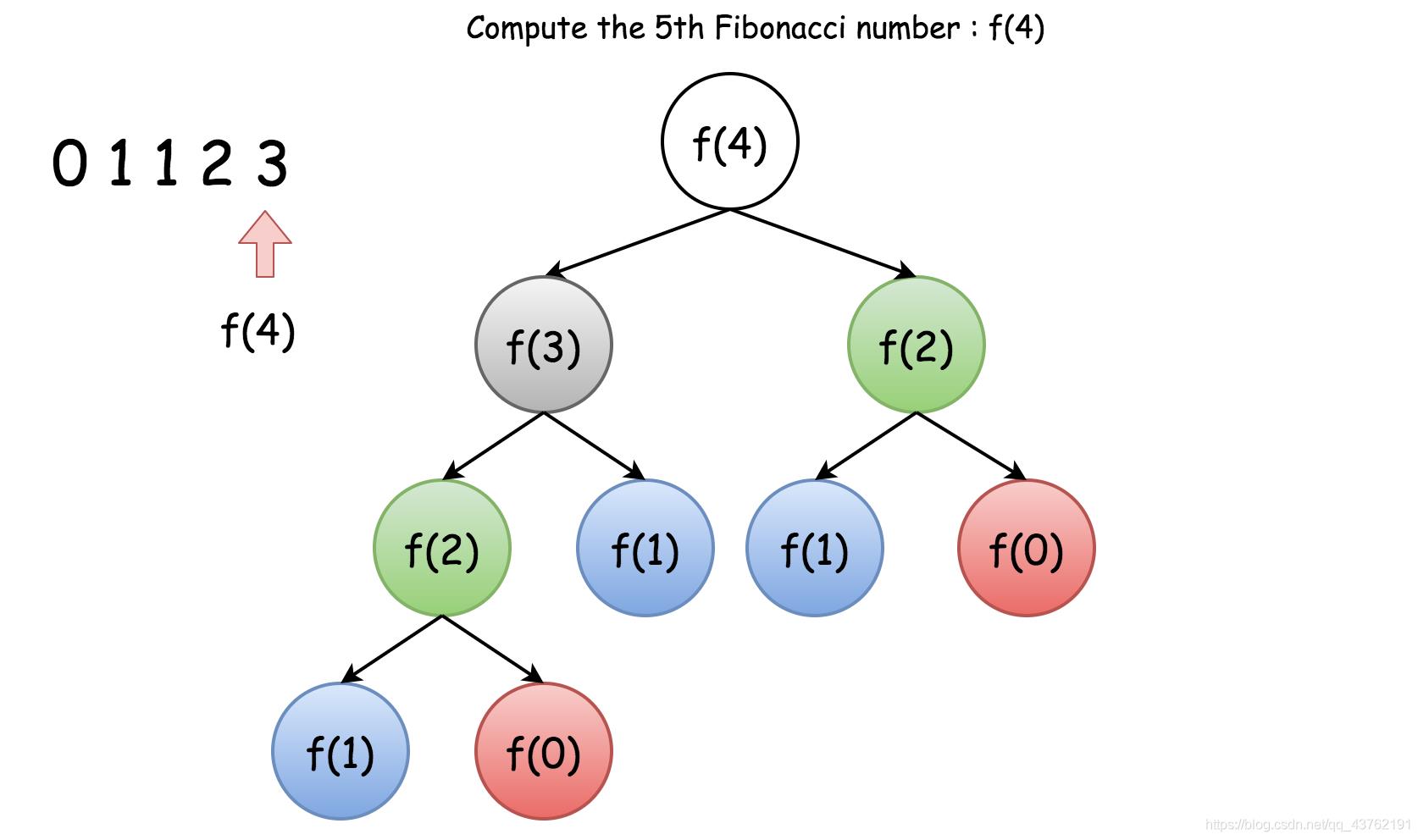
在这里插入图片描述

详细了解递归算法：【C++】算法集锦（2）：递归精讲

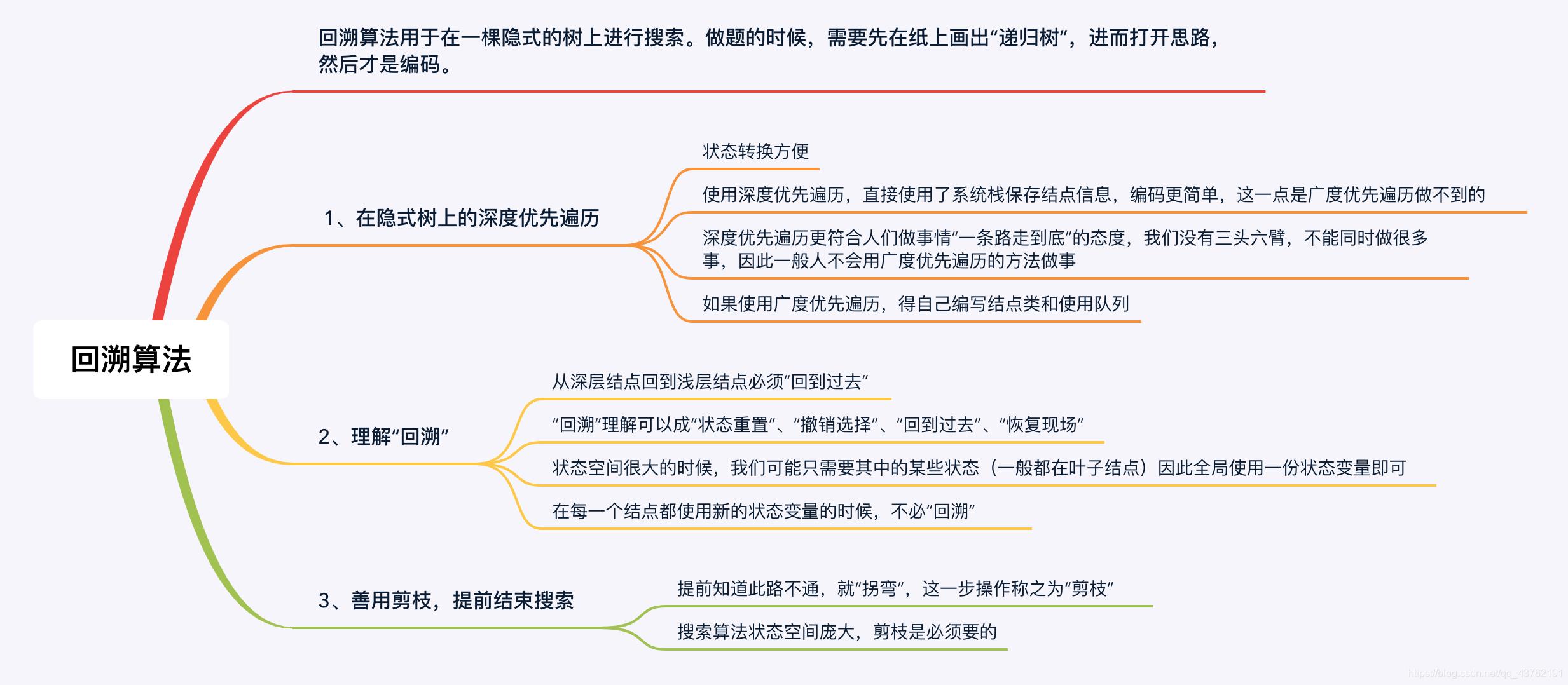
回溯算法

第 1 步都是先画图，画图是非常重要的，只有画图才能帮助我们想清楚递归结构，想清楚如何剪枝。就拿题目中的示例，想一想人手动操作是怎么做的，一般这样下来，这棵递归树都不难画出。

即在画图的过程中思考清楚：
1、分支如何产生；
2、题目需要的解在哪里？是在叶子结点、还是在非叶子结点、还是在从跟结点到叶子结点的路径？
3、哪些搜索是会产生不需要的解的？例如：产生重复是什么原因，如果在浅层就知道这个分支不能产生需要的结果，应该提前剪枝，剪枝的条件是什么，代码怎么写？

在这里插入图片描述

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/
来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

更进一步了解回溯算法：【C++】算法集锦（3）：回溯，从入门到入土，七道试题精选、精讲、精练

动态规划

不扯那些弯弯绕的。
第一步：画出暴力解法流程。
第二步：画出决策树（看着直观）
第三步：写出状态转移方程
第四步：决策树剪枝
第五步：再优化：确定边界

这五步列在这里，并不是说每一步都要严格的执行，我们的目标是解决问题，解决动态规划问题就需要状态转移方程，要写出好的状态转移方程就需要决策树以及决策树的剪枝优化，要画出决策树，最好有个暴力解的流程图。

不要看不起暴力求解，动态规划问题最困难的就是写出状态转移方程，即这个暴力解。优化方法无非是用备忘录或者 DP table，再无奥妙可言。

以练养学：【C++】算法集锦（4）：给人看的动态规划

广度优先遍历

BFS算法和DFS算法属于图论算法的范畴，DFS在前面回溯中，可以去看一下。
BFS算法用于寻找两点之间的最短路径。

碧如说：寻找树的最小高度（迭代法）、走迷宫、导航等问题。
这些问题看起来都会比较抽象，去做也是很抽象。

与其说算法框架难写，倒不如说是把实际问题转化为算法问题来的要难。
还记得我在图论算法那篇里面有讲过：学习图论算法，最难的是要有用图论算法的意识。等下看了例题就知道了。

代码框架：

int BFS(Node start,Node target){
	/*
		这是一个BFS算法的代码框架
		return：返回从start到target的最短步数
		start：起始点
		target：终点
	*/
	
	Queue<Node> q;
	Set<Node> visited;	//避免走回头路
	
	q.offer(start);	//将起点加入队列
	visited.add(start);
	int step = 0;	//纪录扩散的步数

	while(q not empty){
		int sz = q.size();
		for(int i = 0; i<sz; i++){
			Node cur = q.poll();

			//判断是否到终点
			if(cur is target)
				return step;
			
			//将cur相邻节点加入队列
			for(Node x: cur.adj())	//cur.adj()泛指与cur相邻的节点
				if(x not in visited){
					q.offer(x);
					visited.add(x);
				}
		}	
		step++;	//更新步数
	}
}

更多详解：【C++】算法集锦（5）：BFS算法

妙用快慢指针

这个就不用我多介绍吧，前面好多个“算法刷题”的文里面都一直在用了。

【C++】算法集锦（6）：快慢指针

滑动窗口

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组，返回 0。

示例: 

输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。

看到这个题，我不知道大家是怎么想的，我想到的就是暴力解法：
1、从头开始，以每个数字作为结果数组的头，找到刚好能大于s的结果数组。并记下结果数组中 [1:] 的和（Python写法），记为 t 。
2、如果 t 已经大于 s 了，那就结果数组头开始递减，一直减到 t 刚好小于 s 为止。
3、时刻保留一个最短子序列。
4、结果数组往后遍历一格，将值加入 t 当中。
5、回到第二步，直到结果序列的屁股顶到原序列的末位。
6、返回保留的最短子序列的长度。

这是暴力解法吧，不知道为什么他们要叫这种解法为滑动窗口，还给出了不低的难度系数。。
如果看不懂我上面的表述，可以看图：（一图胜千言）

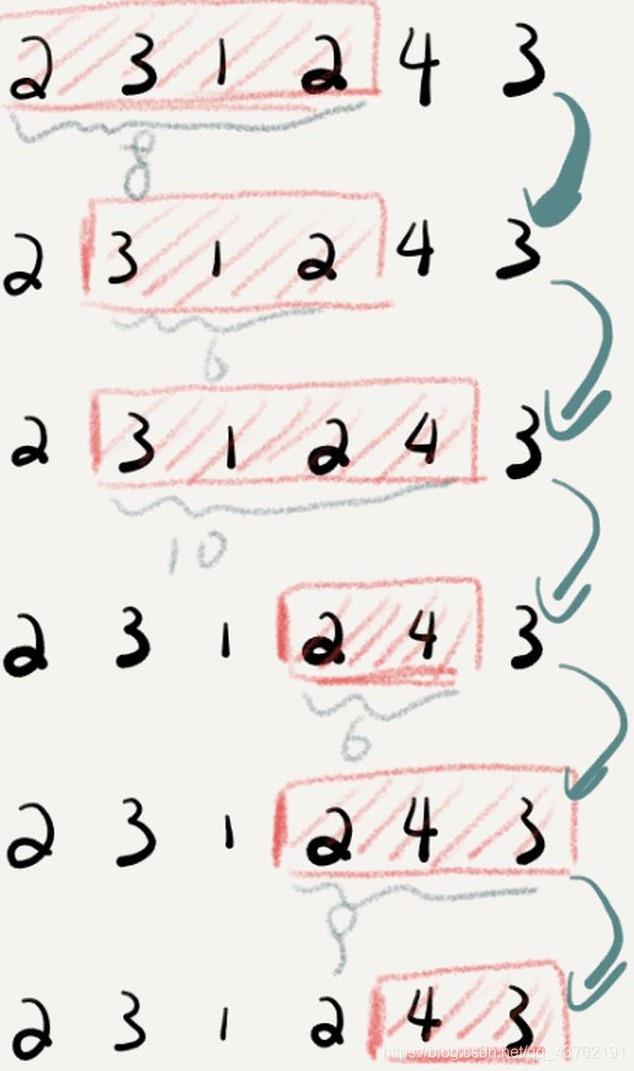
在这里插入图片描述

详解“滑动窗口”算法：【C++】算法集锦（7）滑动窗口

N数和问题

2sum问题：

给定一个数组，以及一个数，从数组里随即找两个数加起来等于给定的那个数。
找出每组符合条件的数（不可重复）。

这表述没有问题吧。

那，这样的题目该怎么实现呢？

如果看过上一篇，的上一篇的小伙伴应该很快就能想到用双指针吧（其实那篇我就想写这个了，但是想了想，还是憋住了）

这里有两个地方要注意：
1、数组要有序
2、跳过同类项

然后，就没什么难度了吧，我把伪代码写一下：

def two_sum(sum,nums):
	ret = []
	sz = len(nums)
	i = 0
	j = sz-1
	while i<j:
		if nums[i]+nums[j] == sum:
			ret.append([nums[1],nums[j]])
		elif nums[i]+nums[j] > sum:
			while nums[j-1] == nums[j]:
				j-=1
			j-=1
		else:
			while nums[i+1] == nums[i]:
				i+=1
			i+=1
	
	return ret