数学 函数 图形
Posted 流星蝴蝶没有剑
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学 函数 图形相关的知识,希望对你有一定的参考价值。
数学函数对应的图形
下面函数介绍可能会有描述错误,请指出
没有多余介绍,重点是大概了解函数的图形
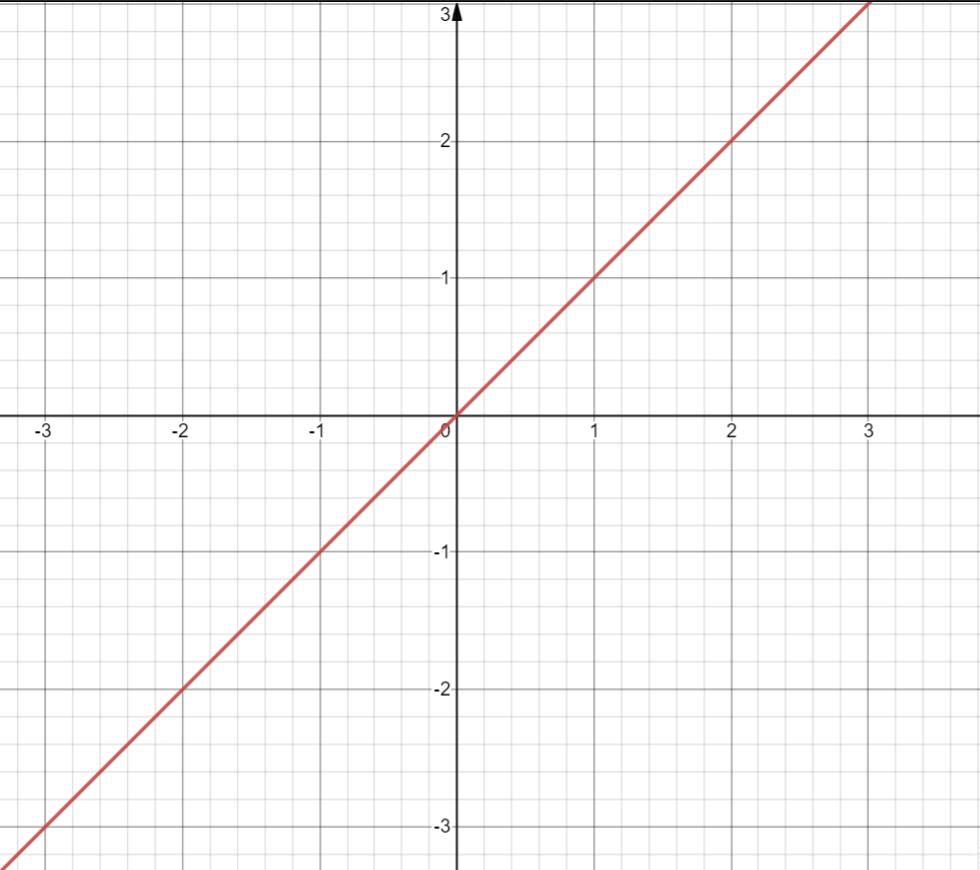
1. y =x
定义域 R
值域 R
奇函数
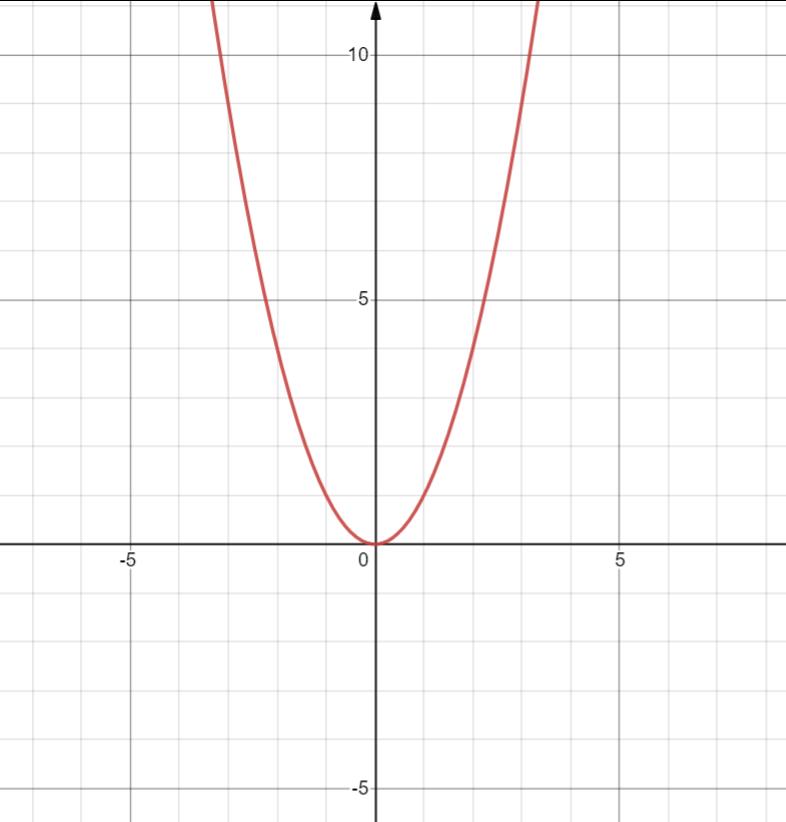
2. y = x2
定义域 R
值域 R
偶函数
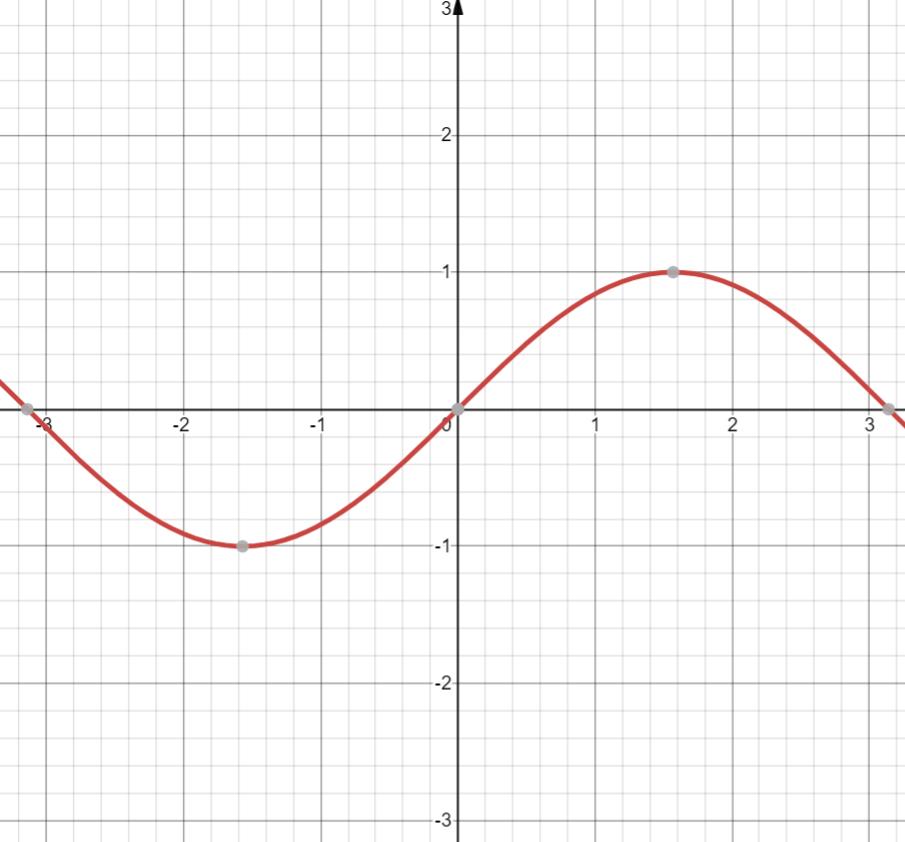
3. y = sinx
定义域 R
值域 [-1,1]
奇函数
周期 2
π
\\pi
π
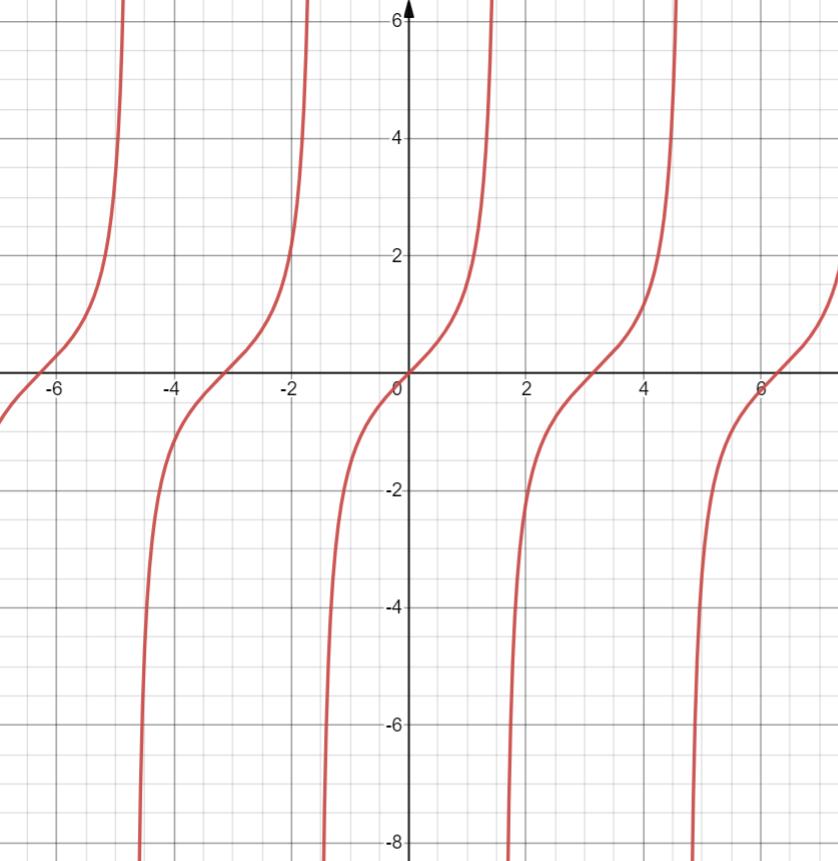
4. y = tanx
定义域 x
≠
\\ne
=
π
2
\\frac \\pi 2
2π + n
π
\\pi
π
值域 R
奇函数
周期
π
\\pi
π
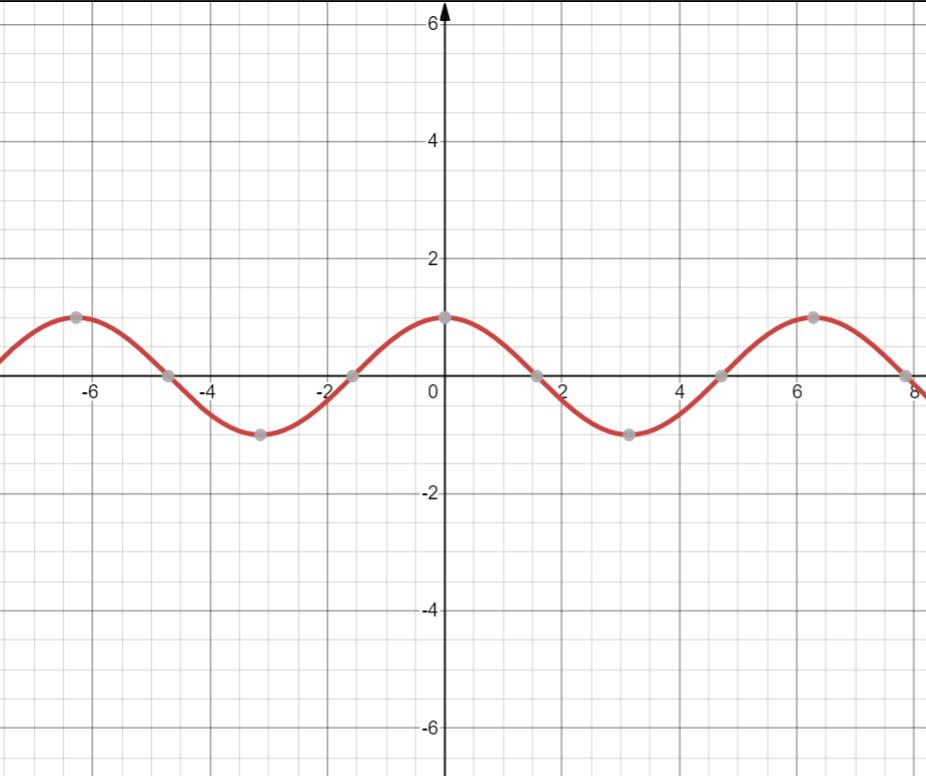
5. y = cosx
定义域 R
值域 [-1,1]
偶函数
周期 2
π
\\pi
π
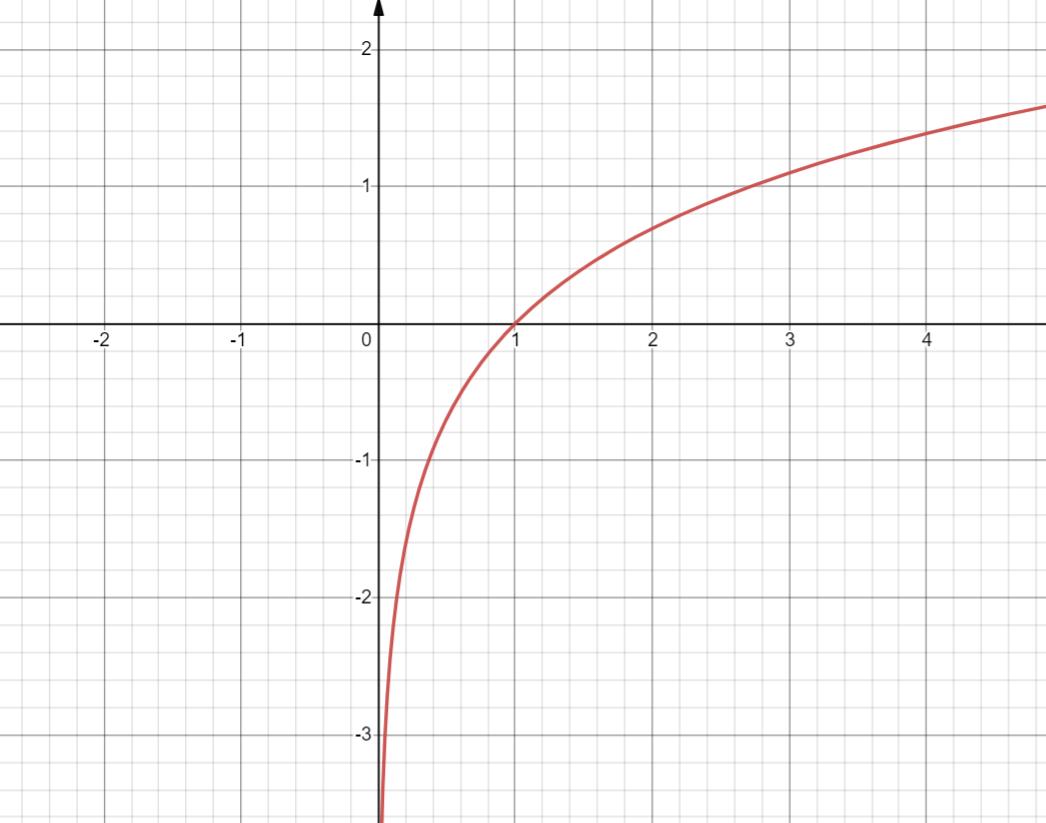
6. y = lnx
定义域 (0,+
∞
\\infin
∞)
值域 [-1,1]
偶函数
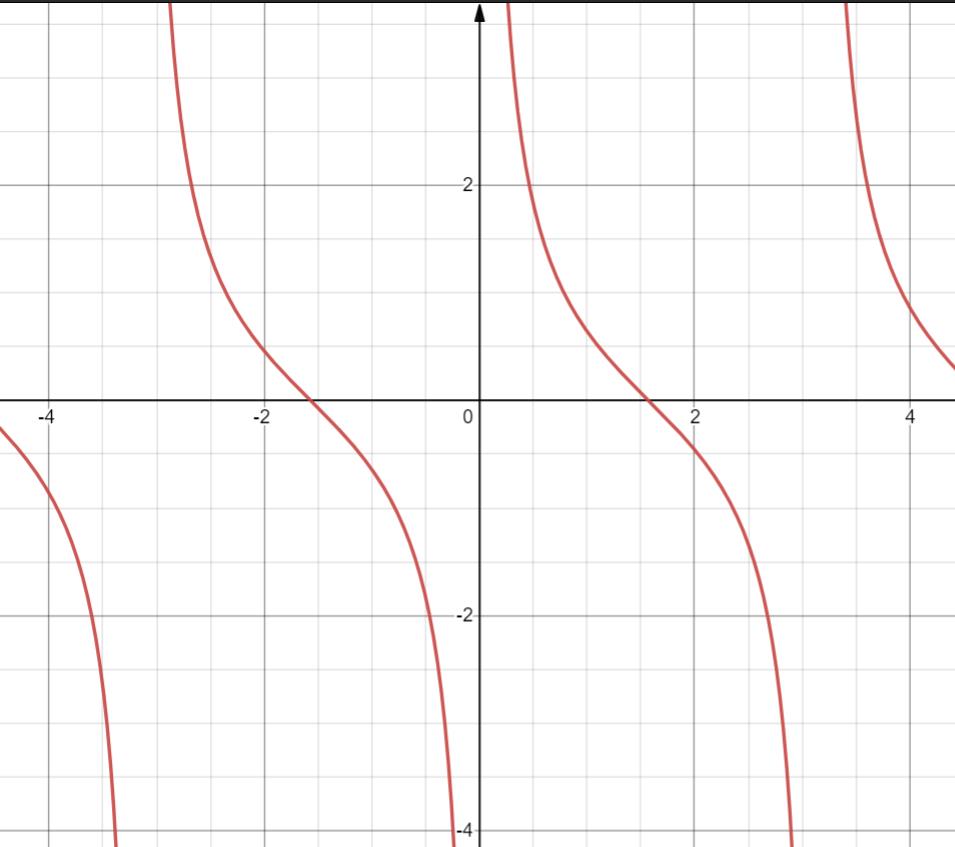
7. y = cotx = 1 t a n x \\frac 1 {tanx} tanx1
定义域 x
≠
\\ne
=n
π
\\pi
π
值域 R
奇函数
周期
π
\\pi
π
8. y = cscx = 1 s i n x \\frac 1 {sinx} sinx1
定义域 x
≠
\\ne
= n
π
\\pi
π
值域 x≥1, x≤-1
奇函数
周期 2
π
\\pi
π
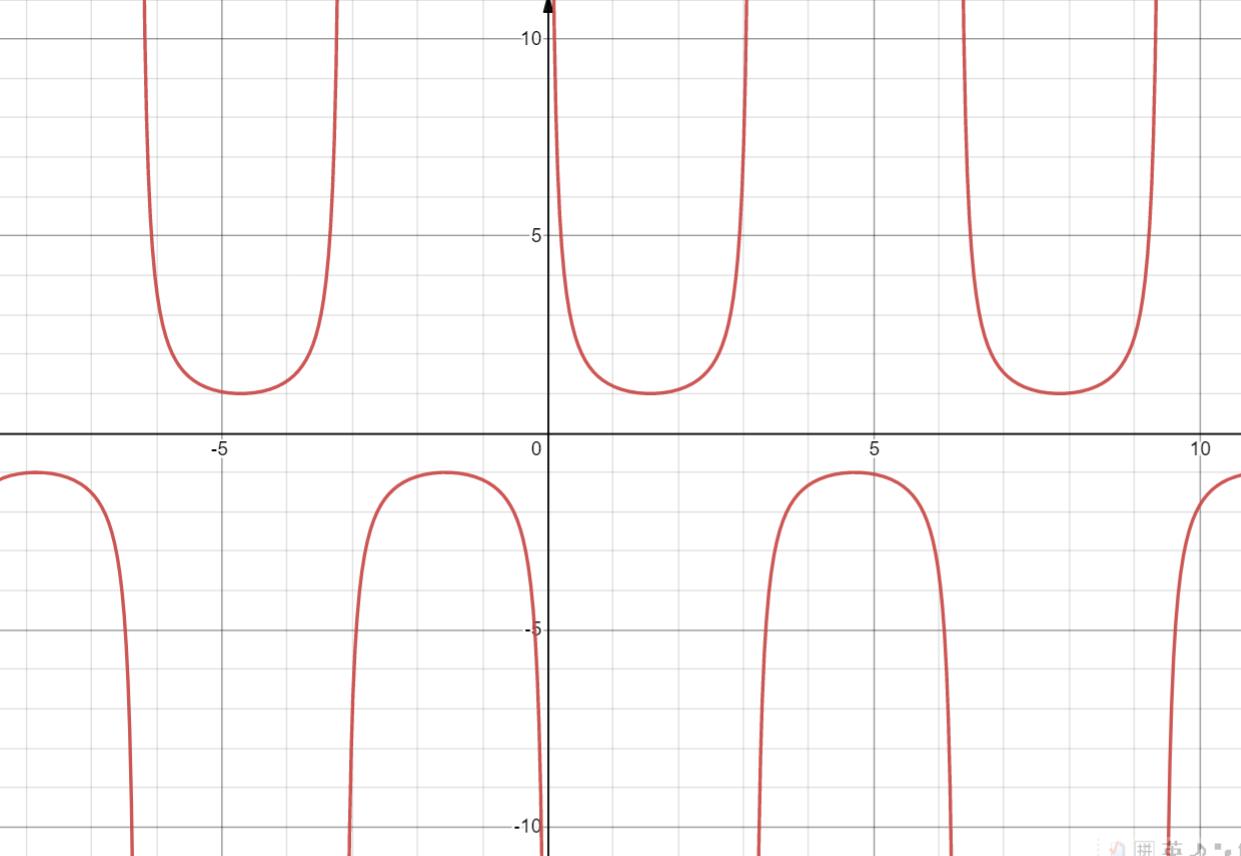
9. y = secx = 1 c o s x \\frac 1 {cosx} cosx1
定义域 x
≠
\\ne
=
π
2
+
n
π
\\frac \\pi 2 + n\\pi
2π+nπ
值域 x≥1 , x≤-1
偶函数
周期 2
π
\\pi
π
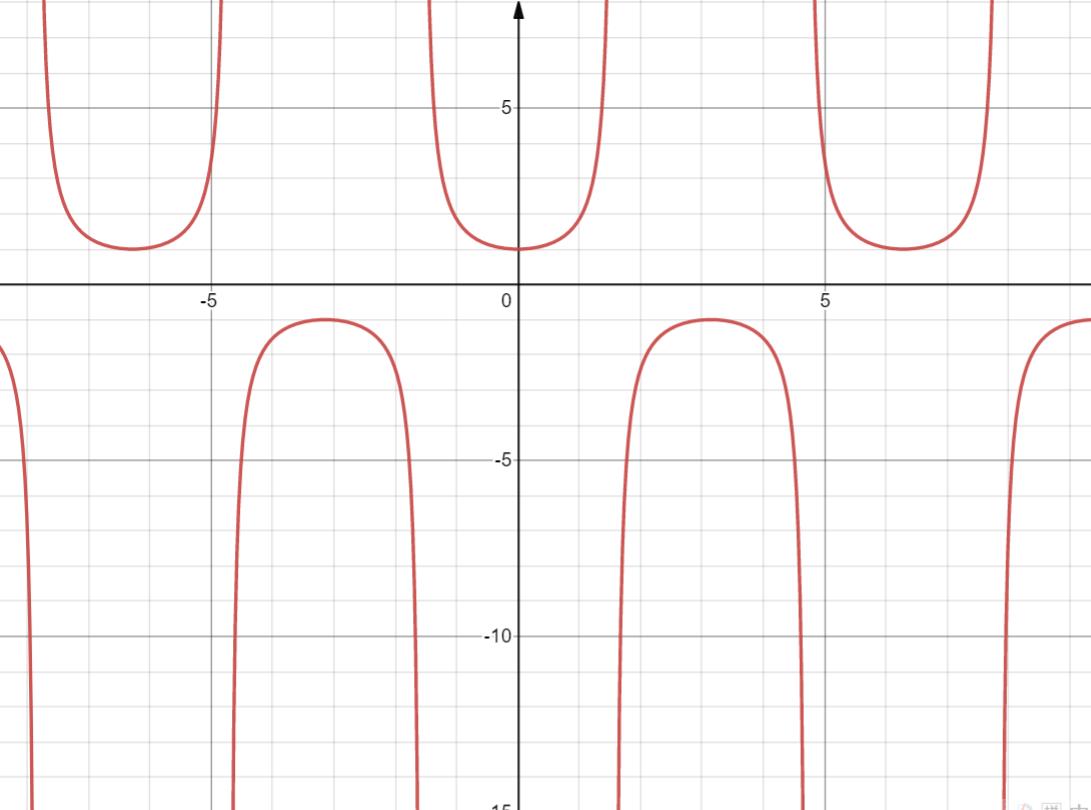
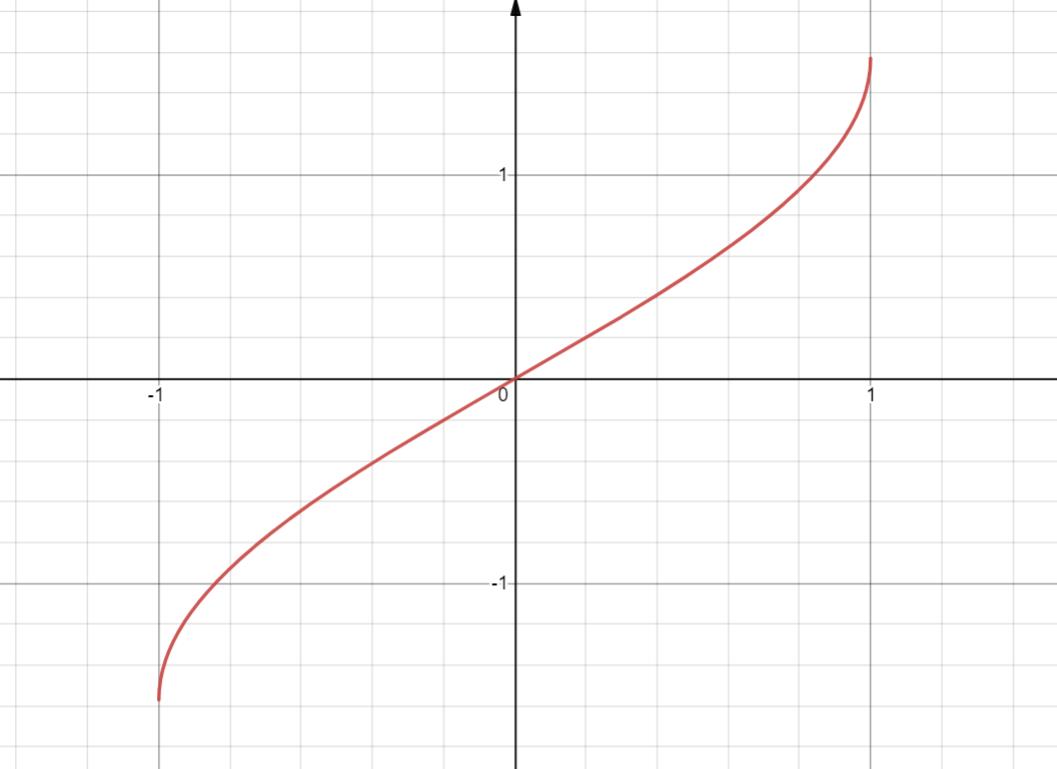
10. y = arcsinx
定义域 [-1, 1]
值域 [
−
π
2
,
π
2
-\\frac \\pi 2 , \\frac \\pi 2
−2π,2π]
奇函数
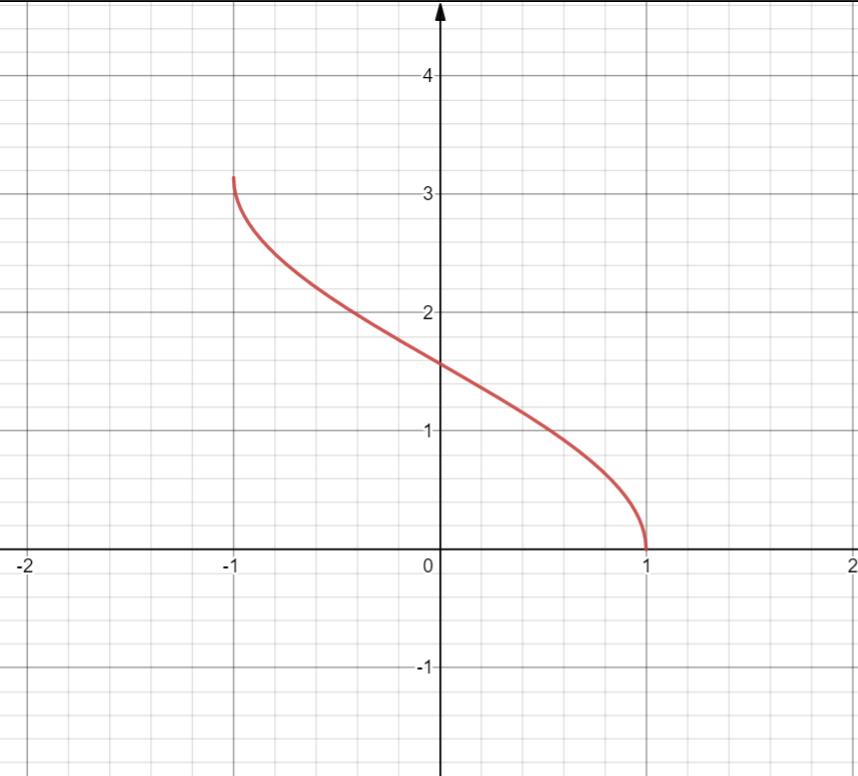
11. y = arccosx
x=cosy
定义域 [-1, 1]
值域 [
0
,
π
0 , \\pi
0,π]
12. y = arctanx
x = tany
定义域 R
值域 (
−
π
2
,
π
2
-\\frac \\pi 2 , \\frac \\pi 2
−2π,2π)
奇函数
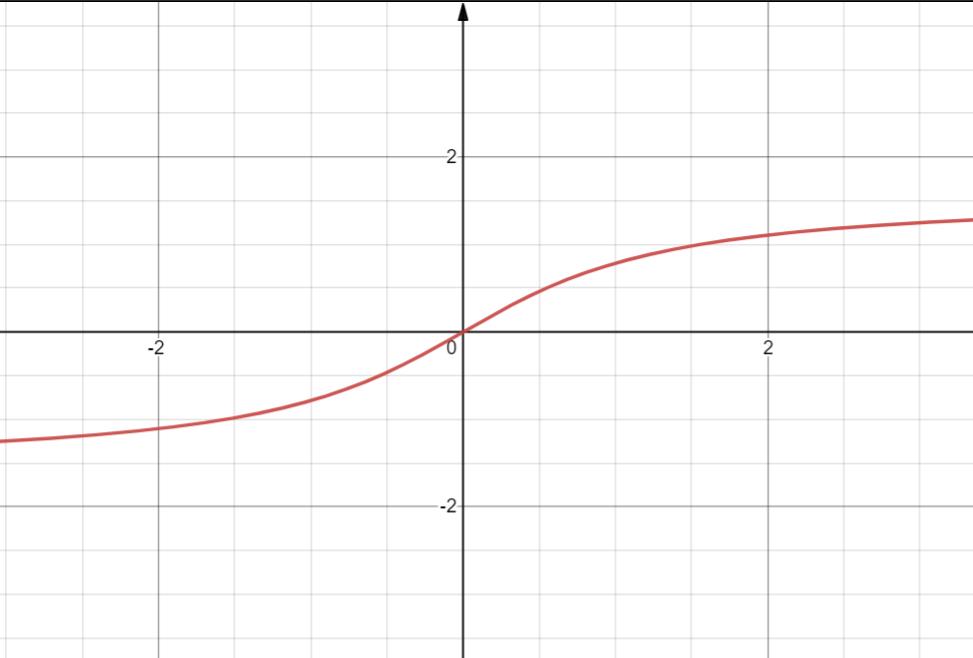
13. y = arccotx
x = coty
定义域 R
值域 (
0
,
π
0 ,\\pi
0,π)
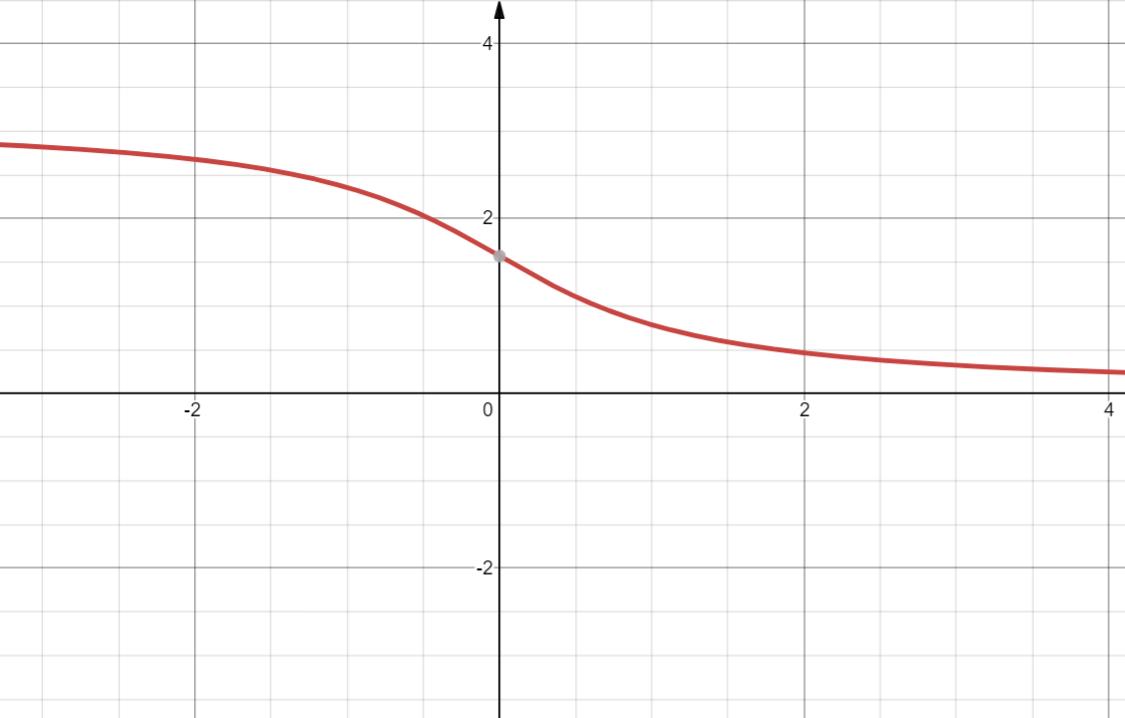
14. y=arccscx.
x = secy
定义域 (-
∞
,
−
1
]
,
[
1
,
+
∞
)
\\infin, -1], [1,+\\infin)
∞,−1],[1,+∞)
值域 [
−
π
2
,
0
-\\frac \\pi 2 ,0
−2π,0) ,(0
,
π
2
, \\frac \\pi 2
,2π)
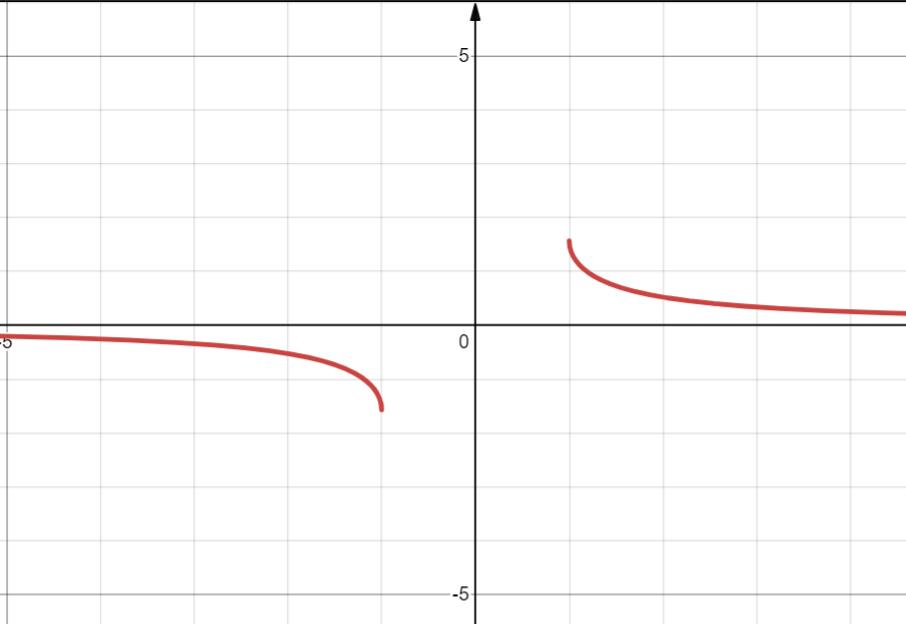
14. y=arcsecx
x = secy
定义域 (-
∞
,
−
1
]
,
[
1
,
+
∞
)
\\infin, -1], [1,+\\infin)
∞,−1],[1,+∞)
值域 [
0
,
π
2
)
,
(
π
2
,
π
0 ,\\frac \\pi 2) ,(\\frac \\pi 2, \\pi
0,2π),(2π,π]
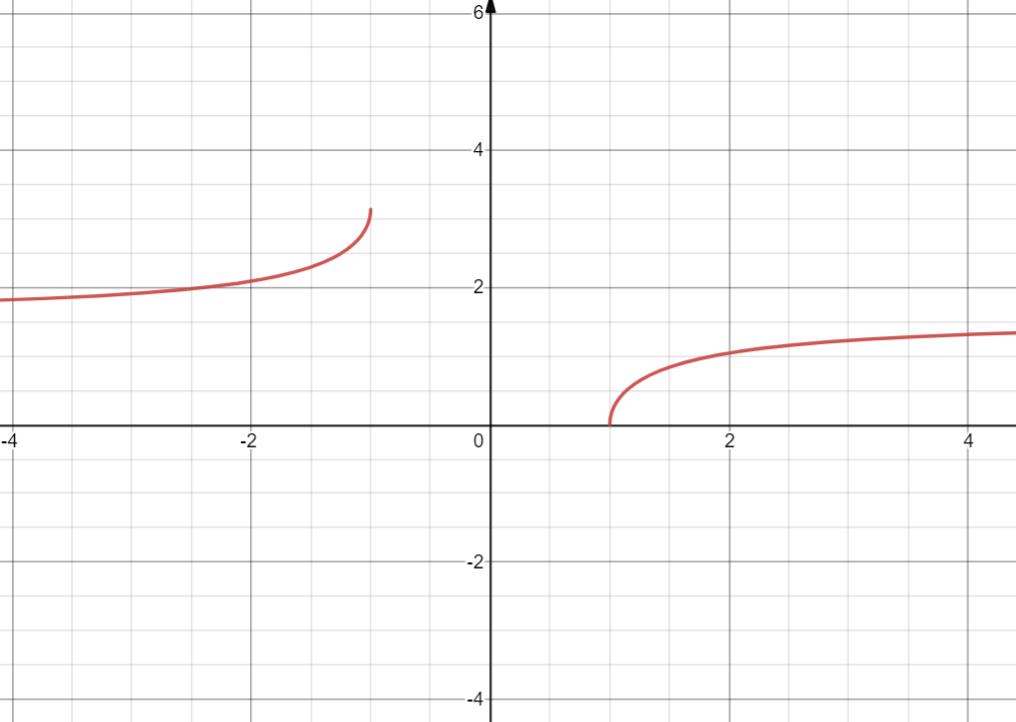
15. y = ex
定义域 R
值域 (
0
,
+
∞
0 , +\\infin
0,+∞)
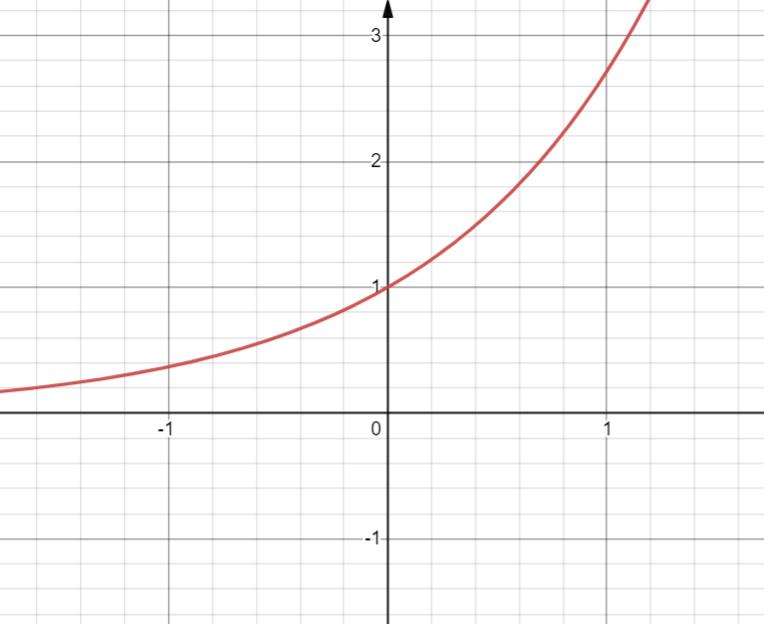
16. y=( e x − e − x 2 \\frac {e^x-e^{-x}} 2 2ex−e−x) = shx = sinh x
双曲正弦
定义域 R
值域 R
奇函数
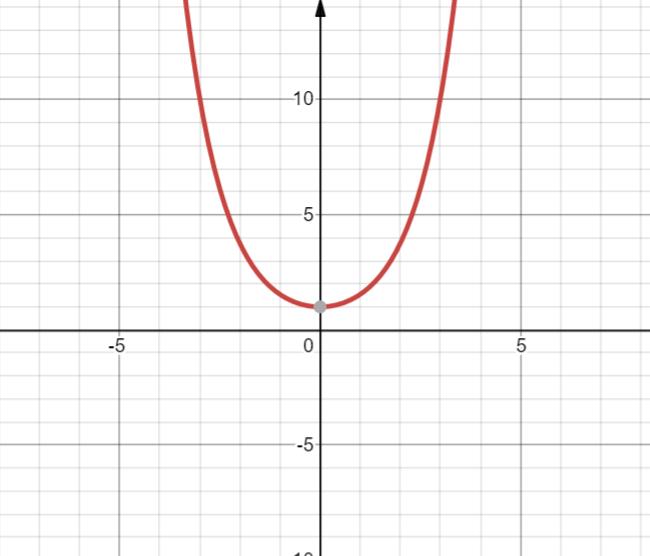
17. y=( e x + e − x 2 \\frac {e^x+e^{-x}} 2 2ex+e−x) = chx = cosh x
双曲余弦
定义域 R
值域 R
偶函数
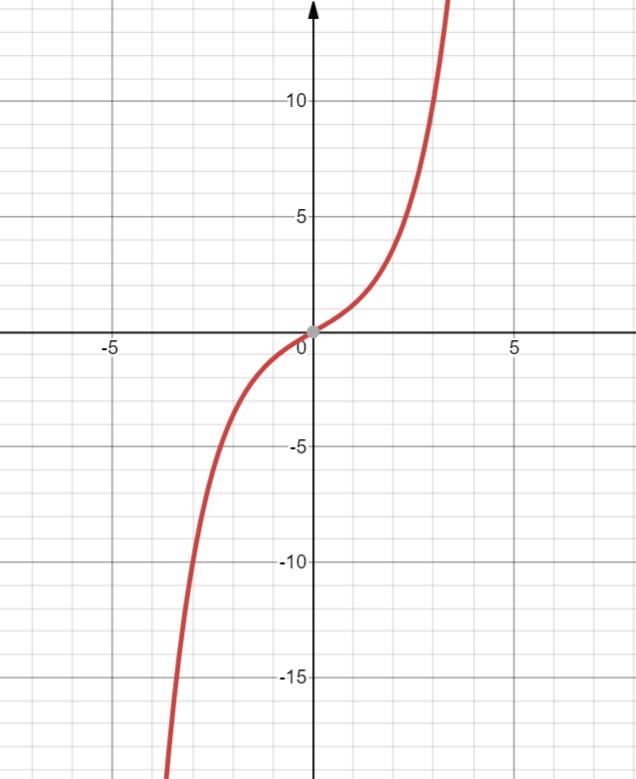
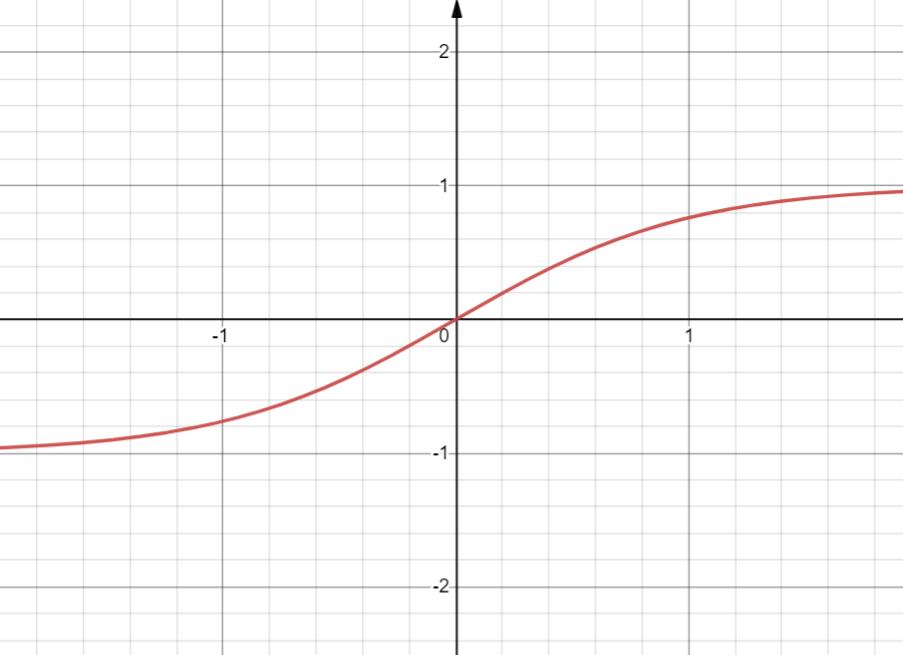
18. y=( e x − e − x e x + e − x \\frac {e^x-e^{-x}} {e^x+e^{-x}} ex+e−xex−e−x) = thx = tanh x
双曲正切
定义域 R
值域 (-1,1)
奇函数
19. y=coth x = 1 t h x \\frac 1 {thx} thx1
双曲余切
定义域 x!=0
值域
(
−
∞
,
−
1
)
,
(
1
,
+
∞
)
(-\\infin,-1), (1,+\\infin)
(−∞,−1),(1,+∞)
奇函数
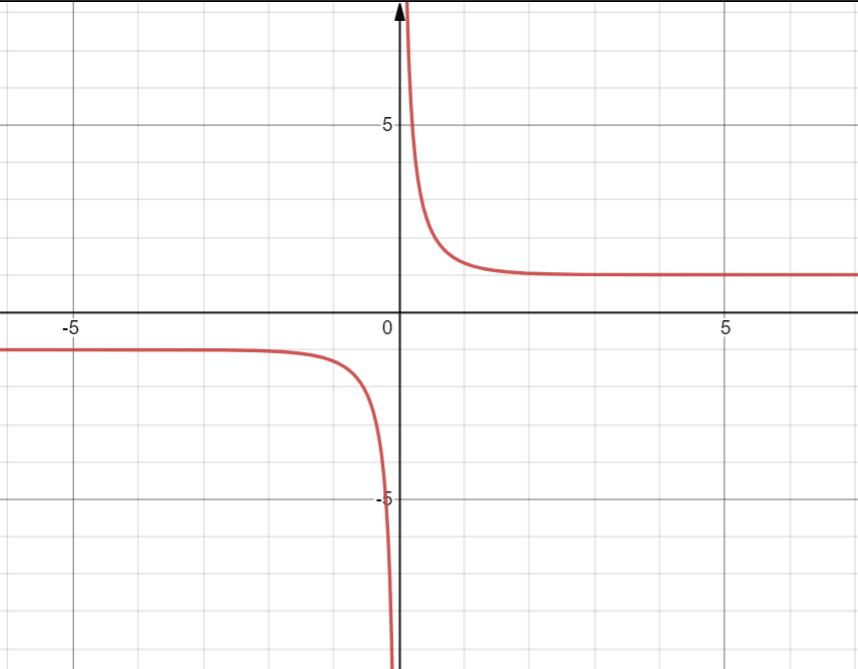
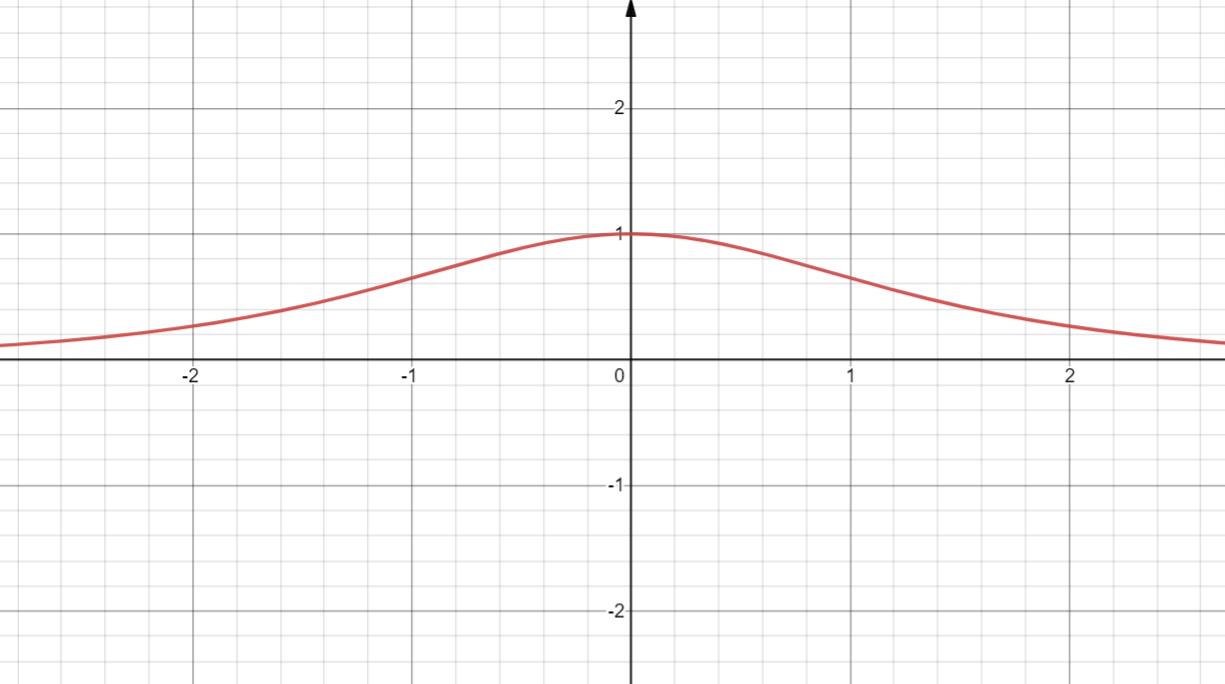
20. y=sech x = 1 c h x \\frac 1 {ch x} chx1
双曲正割
定义域 R
值域
(
0
,
1
]
(0,1]
(0,1]
偶函数
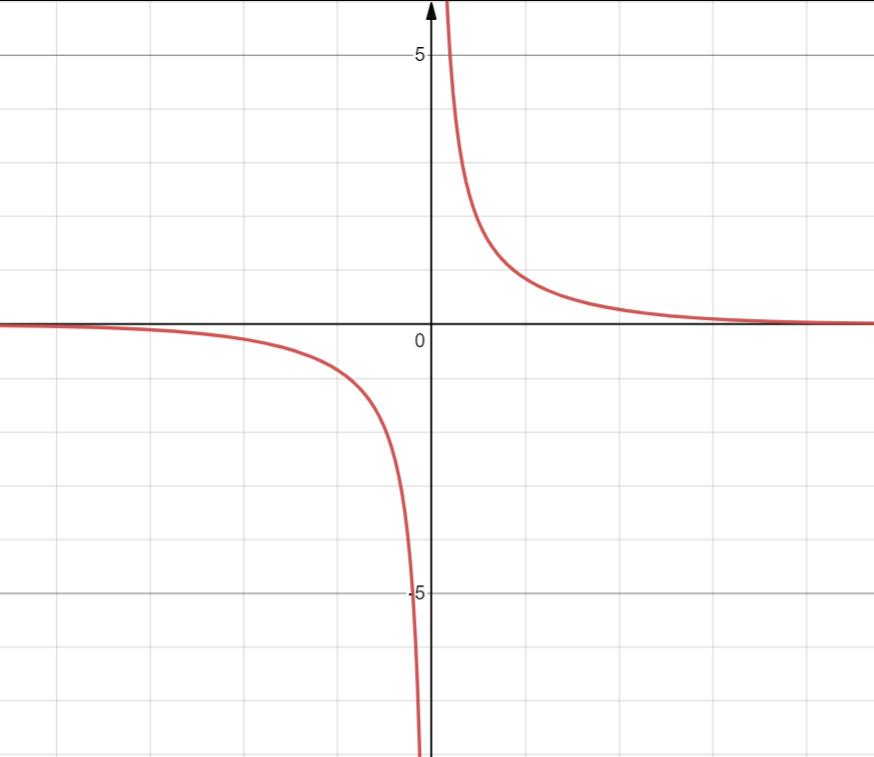
21. y=csch x = 1 s h x \\frac 1 {sh x} shx1
双曲正割
定义域 R
值域
(
0
,
1
]
(0,1]
(0,1]
奇函数
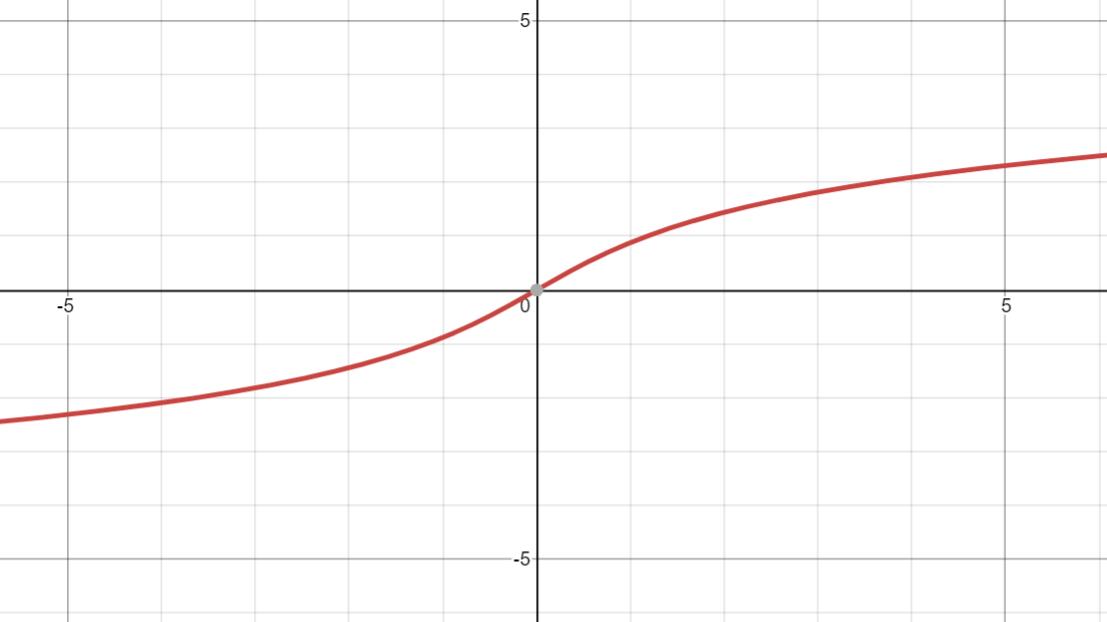
22. y= ln(x+ x 2 + 1 \\sqrt {x^2+1} x2+1) = arcsh x
x=shy
反双曲正弦
定义域R
值域R
奇函数
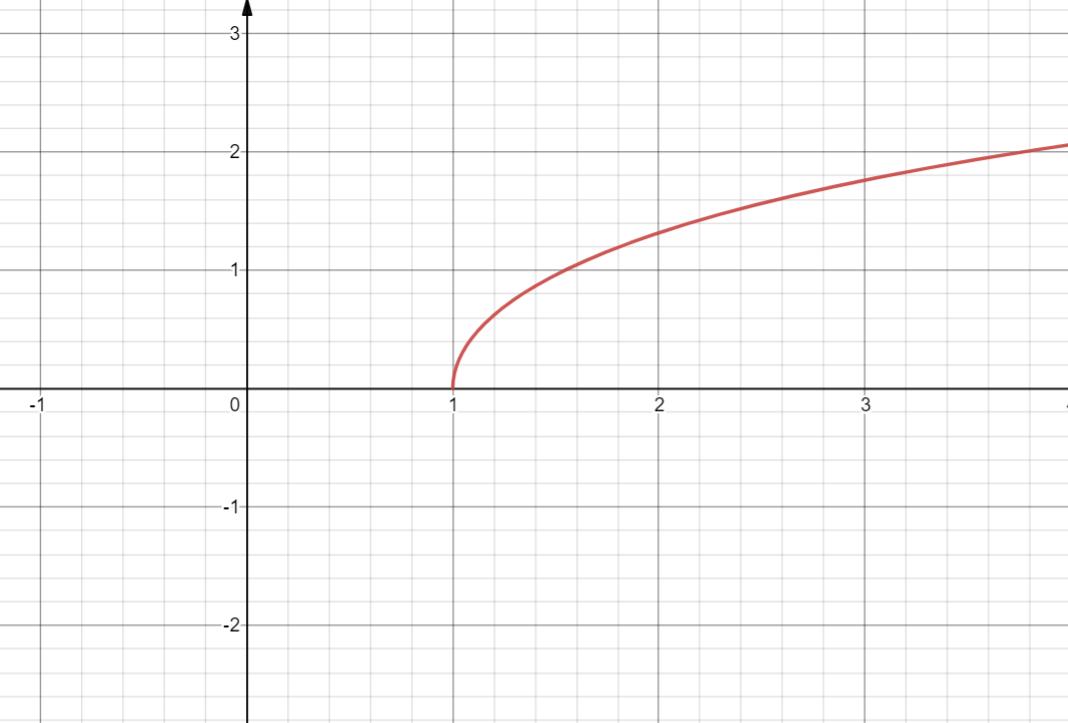
23. y=ln(x+ x 2 − 1 \\sqrt {x^2-1} x2−1) =arcch x
x=chy
反双曲余弦
定义域 [1, +
∞
\\infin
∞)
值域 [0,
+
∞
+\\infin
+∞)
24. y= 1 2 l n 1 + x 1 − x \\frac 1 2 ln\\frac {1+x} {1-x} 21ln1−x1+x =arcth x
x=thy
反双曲正切
定义域为(-1,1)
值域 R
奇函数