优化求解多目标灰狼优化算法MOGWOmatlab源码

Posted Matlab走起

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了优化求解多目标灰狼优化算法MOGWOmatlab源码相关的知识，希望对你有一定的参考价值。

Grey Wolf Optimizer是Seyedali Mirjalili受大灰狼捕食策略的启发，于2014年提出的一种元启发式算法，主要模拟了搜索猎物、包围猎物和攻击猎物，源代码关注公众号后，回复"灰狼"或"GWO"获取。

启发

灰狼属于犬科动物，是食物链顶端的顶级掠食者，它们大多喜欢群居生活，每个种群平均5~12不等。特别有趣的是，它们有非常严格的社会等级，如下图所示。

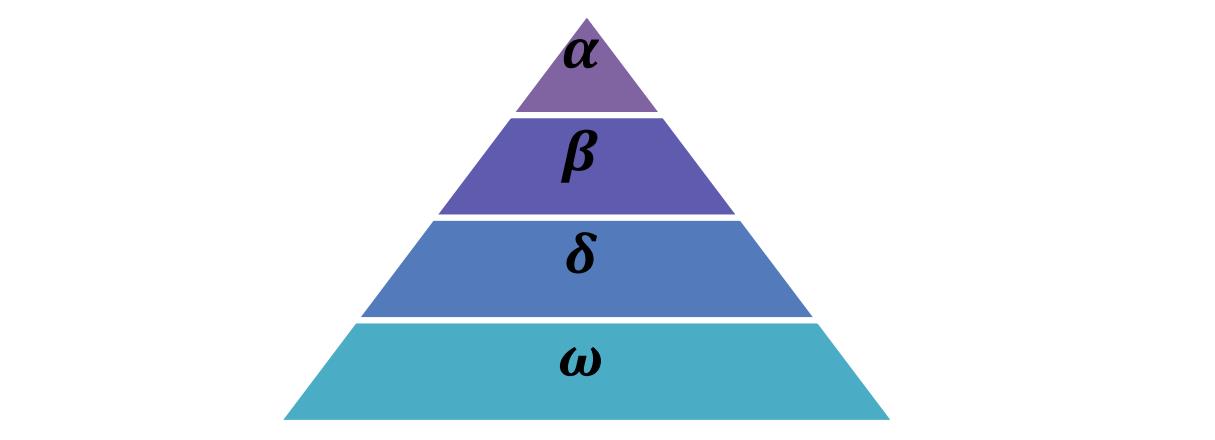
图1 灰狼分层

领头狼（领导者）是一公一母，称为alphas（个人理解，之所以这么叫，是因为alpha是希腊字幕中的第一个，用来表示最前面的）。alpha狼主要负责决策狩猎、睡觉地点、起床时间等等，然后再将决策下达至整个种群，如果狼群垂下尾巴说明它们都认可。然而种群中也会存在民主行为，alpha狼也会听从种群中的其他狼。有趣的是，alpha狼不一定是最强壮的成员，但在管理团队方面是最好的。这说明一个狼群的组织和纪律远比它的力量重要。

第二层是beta。deta狼是从属狼，可公可母，用于辅助alpha狼制定决策或其他种群活动。当其中一只alpha狼去世或变老时，它就是alpha狼的最佳替补。beta狼应该遵从alpha狼，但也会命令其他低级别的狼，因而起到承上启下的作用。

最底层的是omega狼。它们扮演了"替罪羊"的角色（好惨）,必须屈服于其他领头狼，进食时也是排在最后。看起来omega狼在狼群中并不是一个重要的个体，但是一旦失去omega狼，整个狼群就会面临内部争斗和问题。

如果一头狼既不是alpha，beta，也不是omega，就称为从属狼或delta狼。delta狼必须听从于alpha和beta狼，但会支配omega狼。侦察狼、守卫狼、老狼、捕食狼和看管狼都是这一类。侦察狼负责监视领地的边界，一旦有危险就向狼群发出警告；守卫狼保护和保证狼群的安全；老狼是从alpha或beta退下来的经验丰富的狼；捕食狼帮助alpha和beta捕猎并为狼群提供食物；看管狼负责照顾狼群中的老弱病残。

除此之外，群体狩猎是灰狼的另一个有趣的社会行为，主要包括以下几个阶段：

  • 跟踪、追逐和接近猎物；
  • 追捕、包围和骚扰猎物，直到它停止移动；
  • 向猎物发起攻击。

图2 灰狼捕食行为：(A)追逐、接近和跟踪猎物。(B-D)追捕、骚扰和包围猎物。(E)静止状态与攻击

 

数学模型和算法

首先给出社会等级、跟踪、包围和攻击猎物的数学模型，然后再提供完整的GWO算法。

社会等级

为了在设计GWO时对狼的社会等级进行数学建模，认为最合适的解是alpha(α \\alphaα)，那么第二和第三最优解分别表示为beta(β \\betaβ)和delta(δ \\deltaδ),而剩余其他解都假定为omega(ω \\omegaω)。在GWO中，通过α \\alphaα、β \\betaβ和δ \\deltaδ来导引捕食（优化），ω \\omegaω听从于这三种狼。

包围捕食

灰狼在捕食时会将猎物包围，使用下式进行表达这种行为：

D ⃗ = ∣ C ⃗ ⋅ X p → ( t ) − X ⃗ ( t ) ∣ (1) \\vec{D}=|\\vec{C} \\cdot \\overrightarrow{X_{p}}(t)-\\vec{X}(t)|\\tag{1}D=∣C⋅Xp​​(t)−X(t)∣(1)

X ⃗ ( t + 1 ) = X p → ( t ) − A ⃗ ⋅ D ⃗ (2) \\vec{X}(t+1)=\\overrightarrow{X_{p}}(t)-\\vec{A} \\cdot \\vec{D}\\tag{2}X(t+1)=Xp​​(t)−A⋅D(2)

其中t tt表示当前迭代次数，A ⃗ \\vec{A}A和C ⃗ \\vec{C}C为系数向量，X p → \\overrightarrow{X_{p}}Xp​​是猎物的位置向量，X ⃗ \\vec{X}X是灰狼的位置向量。

向量A ⃗ \\vec{A}A和C ⃗ \\vec{C}C的计算如下：
A ⃗ = 2 a ⃗ ⋅ r ⃗ 1 − a ⃗ (3) \\vec{A}=2 \\vec{a} \\cdot \\vec{r}_{1}-\\vec{a}\\tag{3}A=2a⋅r1​−a(3)

C ⃗ = 2 ⋅ r 2 → (4) \\vec{C}=2 \\cdot \\overrightarrow{r_{2}}\\tag{4}C=2⋅r2​​(4)

其中a ⃗ \\vec{a}a的各个分量在迭代过程中线性地从2减少到0，r ⃗ 1 \\vec{r}_{1}r1​和r 2 → \\overrightarrow{r_{2}}r2​​为[0,1]之间的随机向量。

为了清楚地反映等式(1)和(2)的效果，图3(a)中显示了二维的位置向量以及可能的邻域，可以看出，灰狼的位置( X , Y ) (X,Y)(X,Y)可以根据猎物的位置( X ∗ , Y ∗ ) (X^*,Y^*)(X∗,Y∗)进行更新，通过调整A ⃗ \\vec{A}A和C ⃗ \\vec{C}C的值，可以在最优代理周围到达相对于当前位置的不同地方。例如，当A ⃗ = ( 0 , 1 ) \\vec{A}=(0,1)A=(0,1)和C ⃗ = ( 1 , 1 ) \\vec{C}=(1,1)C=(1,1)时，灰狼的新位置为( X ∗ − X , Y ∗ ) (X^*-X,Y^*)(X∗−X,Y∗)。三维空间中也是类似。注意，此处的两张图仅仅展示了A ⃗ = ( 0 , 1 ) \\vec{A}=(0,1)A=(0,1)和C ⃗ = ( 1 , 1 ) \\vec{C}=(1,1)C=(1,1)这一种情况，当随机向量r 1 r_1r1​和r 2 r_2r2​取不同的值时，灰狼可以到达任意两点之间的位置。同时还注意到，A AA的取值不同还会决定灰狼靠近还是远离猎物，后面再详细说明。

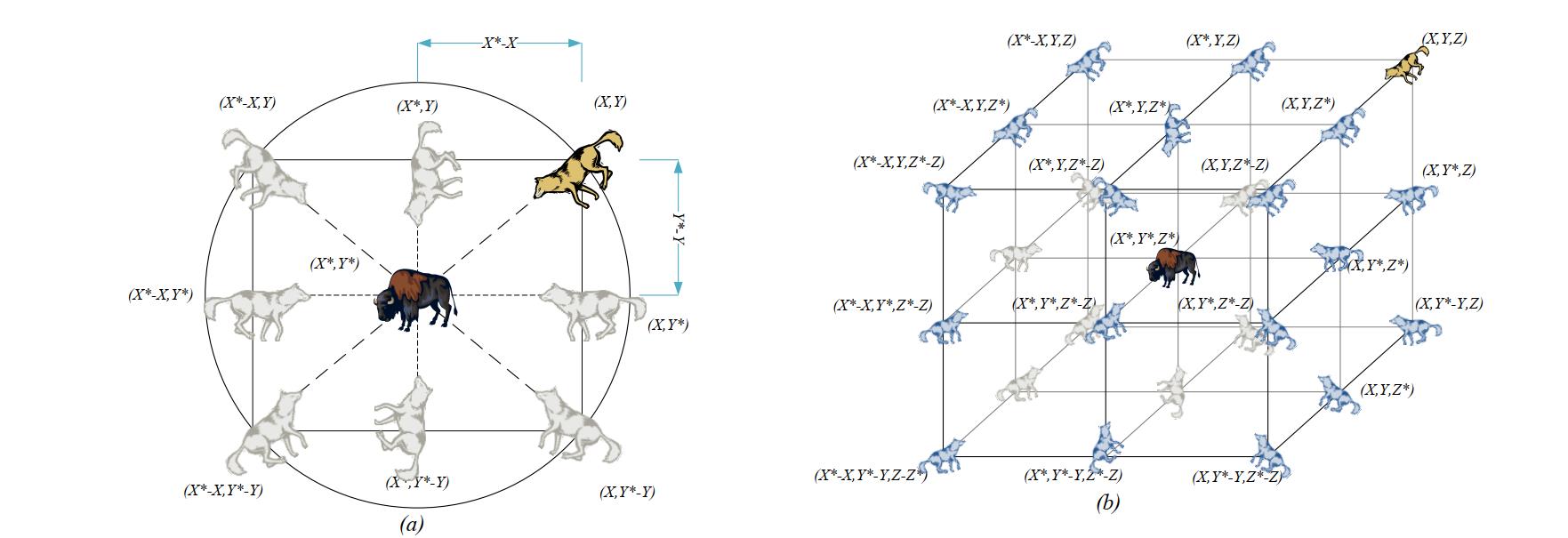
图3 2D和3D位置向量及其可能的下一位置

图3 2D和3D位置向量及其可能的下一位置

 

狩猎

灰狼能够识别猎物的位置并包围它们，狩猎通常是是由alpha狼领导的，beta和和delta狼偶尔也会参与狩猎。然而，在一个抽象的搜索空间中，我们不知道最佳(猎物)的位置。为了在数学上模拟灰狼的狩猎行为，我们假设alpha(最佳候选解)、beta和delta狼对猎物的潜在位置有更好的了解。因此，我们保存到目前为止获得的前三个最佳解，并迫使其他搜索代理(包括omegas)根据最佳搜索代理的位置更新其位置。对此，提出以下公式：

D α → = ∣ C ⃗ 1 ⋅ X α → − X ⃗ ∣ , D β → = ∣ C ⃗ 2 ⋅ X β → − X ⃗ ∣ , D δ → = ∣ C 3 → ⋅ X δ → − X ⃗ ∣ (5) \\overrightarrow{D_{\\alpha}}=\\left|\\vec{C}_{1} \\cdot \\overrightarrow{X_{\\alpha}}-\\vec{X}\\right|, \\overrightarrow{D_{\\beta}}=\\left|\\vec{C}_{2} \\cdot \\overrightarrow{X_{\\beta}}-\\vec{X}\\right|, \\overrightarrow{D_{\\delta}}=|\\overrightarrow{C_{3}} \\cdot \\overrightarrow{X_{\\delta}}-\\vec{X}|\\tag{5}Dα​​=∣∣∣​C1​⋅Xα​​−X∣∣∣​,Dβ​​=∣∣∣​C2​⋅Xβ​​−X∣∣∣​,Dδ​​=∣C3​​⋅Xδ​​−X∣(5)

X 1 → = X α → − A 1 → ⋅ ( D α → ) , X 2 → = X β → − A 2 → ⋅ ( D β → ) , X 3 → = X δ → − A 3 → ⋅ ( D δ → ) 6 ) (() \\overrightarrow{X_{1}}=\\overrightarrow{X_{\\alpha}}-\\overrightarrow{A_{1}} \\cdot(\\overrightarrow{D_{\\alpha}}), \\overrightarrow{X_{2}}=\\overrightarrow{X_{\\beta}}-\\overrightarrow{A_{2}} \\cdot(\\overrightarrow{D_{\\beta}}), \\overrightarrow{X_{3}}=\\overrightarrow{X_{\\delta}}-\\overrightarrow{A_{3}} \\cdot(\\overrightarrow{D_{\\delta}})\\tag(6)X1​​=Xα​​−A1​​⋅(Dα​​),X2​​=Xβ​​−A2​​⋅(Dβ​​),X3​​=Xδ​​−A3​​⋅(Dδ​​)6)(()

X ⃗ ( t + 1 ) = X 1 → + X 2 → + X 3 → 3 (7) \\vec{X}(t+1)=\\frac{\\overrightarrow{X_{1}}+\\overrightarrow{X_{2}}+\\overrightarrow{X_{3}}}{3}\\tag{7}X(t+1)=3X1​​+X2​​+X3​​​(7)

图4展示了2D空间中如何根据alpha，beta和delta进行代理位置的更新。可以看到，最终位置将是圆内的一个随机位置，该圆由alpha、beta和delta定义，换句话说，alpha、beta和delta狼对猎物的位置进行估计，而其他狼则再猎物周围随机更新它们的位置。

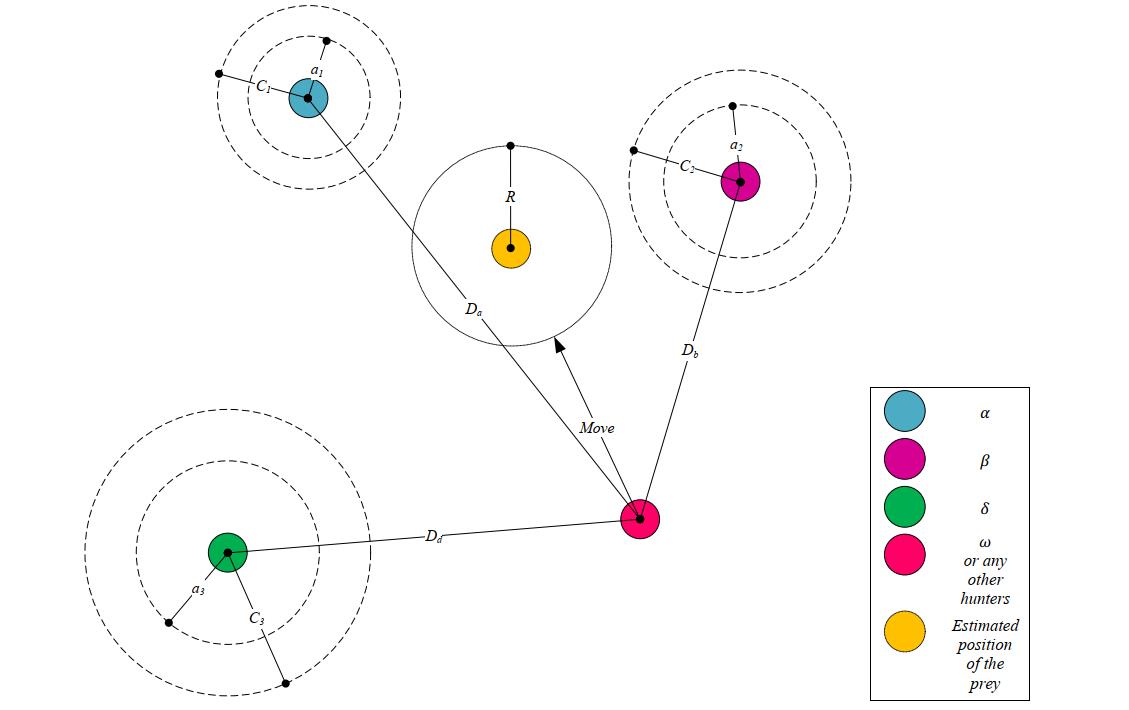
图4 GWO中的位置更新示意图

图4 GWO中的位置更新示意图

攻击猎物（利用）

正如上面提到的，当猎物停止移动时，灰狼就会攻击它来完成狩猎。为了对接近猎物进行建模，需要不断降低a ⃗ \\vec aa的值，那么A ⃗ \\vec AA的波动范围也会降低。当A ⃗ ∈ [ − 1 , 1 ] \\vec A\\in[-1,1]A∈[−1,1]，搜索代理的下一位置可以是代理当前位置和猎物位置之间的任意位置。图5(a)表明当∣ A ∣ < 1 |A|<1∣A∣<1时，灰狼向猎物发起攻击。

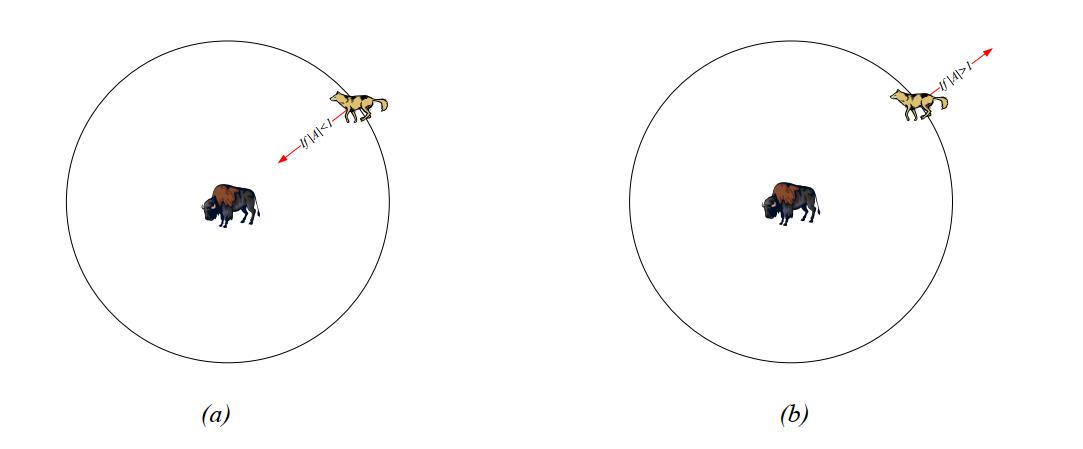
图5 猎物攻击vs搜索猎物

图5 猎物攻击vs搜索猎物

搜索猎物（探索）

灰狼通常根据alpha、beta和delta狼的位置进行搜索，它们彼此分散寻找猎物，然后汇聚攻击猎物。为了数学上对分散建模，利用随机值大于1或小于-1的A ⃗ \\vec AA迫使搜索代理偏离猎物，从而保证了探索。图5(b)表明当∣ A ∣ > 1 |A|>1∣A∣>1时，迫使灰狼离开猎物，希望能找到更合适的猎物。另一个支持GWO进行探索的因素是C ⃗ \\vec CC，根据公式(4)，C ⃗ \\vec CC的取值范围为[ 0 , 2 ] [0,2][0,2]，该分量为猎物提供随机权重，以随机强调(C>1)或弱化(C<1)
猎物在定义等式(1)中的距离时的作用。这有助于GWO在整个优化过程中表现出更随机的行为，有利于探索和避免局部最优。C CC并不是和A AA一样线性递减，特意要求C CC在任何时候都提供随机值，以便不仅在初始迭代中强调探索，而且在最终迭代中也强调探索。

C CC向量也可以被认为是在自然界中障碍物对接近猎物的影响，一般来说，自然中的障碍出现在狼的捕猎路径上，实际上阻碍了它们快速、方便地接近猎物。这就是向量C CC的作用。根据狼所处的位置，它可以随机地给猎物一个权重，从而让狼的捕食变得更加困难和遥远，反之亦然。

GWO算法

总之，搜索过程从在GWO算法中创建一个随机的灰狼种群(候选解)开始。在迭代过程中，alpha、beta和delta狼估计猎物可能的位置。每一个候选解更新它与猎物的距离。为了分别强调探索和利用，将参数a aa从2降低到0。当∣ A ⃗ ∣ > 1 |\\vec A|>1∣A∣>1时,候选解有偏离猎物的倾向，当∣ A ⃗ ∣ < 1 |\\vec A|<1∣A∣<1时,候选解收敛于猎物。最后，当满足结束条件时终止GWO算法。GWO的伪代码如下。

初始化灰狼种群X i ( i = 1 , 2 , . . . , n ) X_i(i=1,2,...,n)Xi​(i=1,2,...,n)

初始化a , A , C a,A,Ca,A,C

计算每个搜索代理的适应度值

X α = X_{\\alpha}=Xα​=最优搜索代理

X β = X_{\\beta}=Xβ​=第二优搜索代理

X δ = X_{\\delta}=Xδ​=第三优搜索代理

while(t<最大迭代次数)

  for 每个搜索代理

    根据等式(7)更新当前代理的位置

  end for

  更新a , A , C a,A,Ca,A,C

  计算所有搜索代理的适应度值

  更新X α X_{\\alpha}Xα​、X β X_{\\beta}Xβ​、X δ X_{\\delta}Xδ​

KaTeX parse error: Expected 'EOF', got '&' at position 1: &̲emsp;&emsp;t=t+…

end while

return X α X_{\\alpha}Xα​

通过以下几点可以了解GWO在理论上是如何解决优化问题的：

  • 所提出的社会等级有助于GWO在迭代过程中保存目前的最优解；
  • 所提出的包围机制在解周围定义了一个圆形邻域，该邻域可以作为超球体扩展到更高维度；
  • 随机参数A AA和C CC辅助候选解具有不同随机半径的超球体；
  • 所提出的狩猎方法允许候选解确定猎物的可能位置；
  • a aa和A AA的适配保证了探索和利用；
  • 参数a aa和A AA的自适应值使GWO在探索和利用之间实现平稳过渡；
  • 随着A AA的下降，一半迭代致力于探索(∣ A ∣ ≥ 1 |A|≥1∣A∣≥1)，另一半致力于利用(∣ A ∣ < 1 |A|<1∣A∣<1)；
  • GWO只有两个主要参数需要调整(a aa和C CC)。
  •  
 
clear all
clc
 
drawing_flag = 1;
 
TestProblem='UF1';
nVar=10;
 
fobj = cec09(TestProblem);
 
xrange = xboundary(TestProblem, nVar);
 
% Lower bound and upper bound
lb=xrange(:,1)';
ub=xrange(:,2)';
 
VarSize=[1 nVar];
 
GreyWolves_num=100;
MaxIt=1000;  % Maximum Number of Iterations
Archive_size=100;   % Repository Size
 
alpha=0.1;  % Grid Inflation Parameter
nGrid=10;   % Number of Grids per each Dimension
beta=4; %=4;    % Leader Selection Pressure Parameter
gamma=2;    % Extra (to be deleted) Repository Member Selection Pressure
 
% Initialization
 
GreyWolves=CreateEmptyParticle(GreyWolves_num);
 
 
for i=1:GreyWolves_num
    GreyWolves(i).Velocity=0;
    GreyWolves(i).Position=zeros(1,nVar);
    for j=1:nVar
        GreyWolves(i).Position(1,j)=unifrnd(lb(j),ub(j),1);
    end
    GreyWolves(i).Cost=fobj(GreyWolves(i).Position')';
    GreyWolves(i).Best.Position=GreyWolves(i).Position;
    GreyWolves(i).Best.Cost=GreyWolves(i).Cost;
end
 
GreyWolves=DetermineDomination(GreyWolves);
 
Archive=GetNonDominatedParticles(GreyWolves);
 
Archive_costs=GetCosts(Archive);
G=CreateHypercubes(Archive_costs,nGrid,alpha);
 
for i=1:numel(Archive)
    [Archive(i).GridIndex Archive(i).GridSubIndex]=GetGridIndex(Archive(i),G);
end
 
% MOGWO main loop
 
for it=1:MaxIt
    a=2-it*((2)/MaxIt);
    for i=1:GreyWolves_num
        
        clear rep2
        clear rep3
        
        % Choose the alpha, beta, and delta grey wolves
        Delta=SelectLeader(Archive,beta);
        Beta=SelectLeader(Archive,beta);
        Alpha=SelectLeader(Archive,beta);
        
        % If there are less than three solutions in the least crowded
        % hypercube, the second least crowded hypercube is also found
        % to choose other leaders from.
        if size(Archive,1)>1
            counter=0;
            for newi=1:size(Archive,1)
                if sum(Delta.Position~=Archive(newi).Position)~=0
                    counter=counter+1;
                    rep2(counter,1)=Archive(newi);
                end
            end
            Beta=SelectLeader(rep2,beta);
        end
        
        % This scenario is the same if the second least crowded hypercube
        % has one solution, so the delta leader should be chosen from the
        % third least crowded hypercube.
        if size(Archive,1)>2
            counter=0;
            for newi=1:size(rep2,1)
                if sum(Beta.Position~=rep2(newi).Position)~=0
                    counter=counter+1;
                    rep3(counter,1)=rep2(newi);
                end
            end
            Alpha=SelectLeader(rep3,beta);
        end
        
        % Eq.(3.4) in the paper
        c=2.*rand(1, nVar);
        % Eq.(3.1) in the paper
        D=abs(c.*Delta.Position-GreyWolves(i).Position);
        % Eq.(3.3) in the paper
        A=2.*a.*rand(1, nVar)-a;
        % Eq.(3.8) in the paper
        X1=Delta.Position-A.*abs(D);
        
        
        % Eq.(3.4) in the paper
        c=2.*rand(1, nVar);
        % Eq.(3.1) in the paper
        D=abs(c.*Beta.Position-GreyWolves(i).Position);
        % Eq.(3.3) in the paper
        A=2.*a.*rand()-a;
        % Eq.(3.9) in the paper
        X2=Beta.Position-A.*abs(D);
        
        
        % Eq.(3.4) in the paper
        c=2.*rand(1, nVar);
        % Eq.(3.1) in the paper
        D=abs(c.*Alpha.Position-GreyWolves(i).Position);
        % Eq.(3.3) in the paper
        A=2.*a.*rand()-a;
        % Eq.(3.10) in the paper
        X3=Alpha.Position-A.*abs(D);
        
        % Eq.(3.11) in the paper
        GreyWolves(i).Position=(X1+X2+X3)./3;
        
        % Boundary checking
        GreyWolves(i).Position=min(max(GreyWolves(i).Position,lb),ub);
        
        GreyWolves(i).Cost=fobj(GreyWolves(i).Position')';
    end
    
    GreyWolves=DetermineDomination(GreyWolves);
    non_dominated_wolves=GetNonDominatedParticles(GreyWolves);
    
    Archive=[Archive
        non_dominated_wolves];
    
    Archive=DetermineDomination(Archive);
    Archive=GetNonDominatedParticles(Archive);
    
    for i=1:numel(Archive)
        [Archive(i).GridIndex Archive(i).GridSubIndex]=GetGridIndex(Archive(i),G);
    end
    
    if numel(Archive)>Archive_size
        EXTRA=numel(Archive)-Archive_size;
        Archive=DeleteFromRep(Archive,EXTRA,gamma);
        
        Archive_costs=GetCosts(Archive);
        G=CreateHypercubes(Archive_costs,nGrid,alpha);
        
    end
    
    disp(['In iteration ' num2str(it) ': Number of solutions in the archive = ' num2str(numel(Archive))]);
    save results
    
    % Results
    
    costs=GetCosts(GreyWolves);
    Archive_costs=GetCosts(Archive);
    
    if drawing_flag==1
        hold off
        plot(costs(1,:),costs(2,:),'k.');
        hold on
        plot(Archive_costs(1,:),Archive_costs(2,:),'rd');
        legend('Grey wolves','Non-dominated solutions');
        drawnow
    end
    
end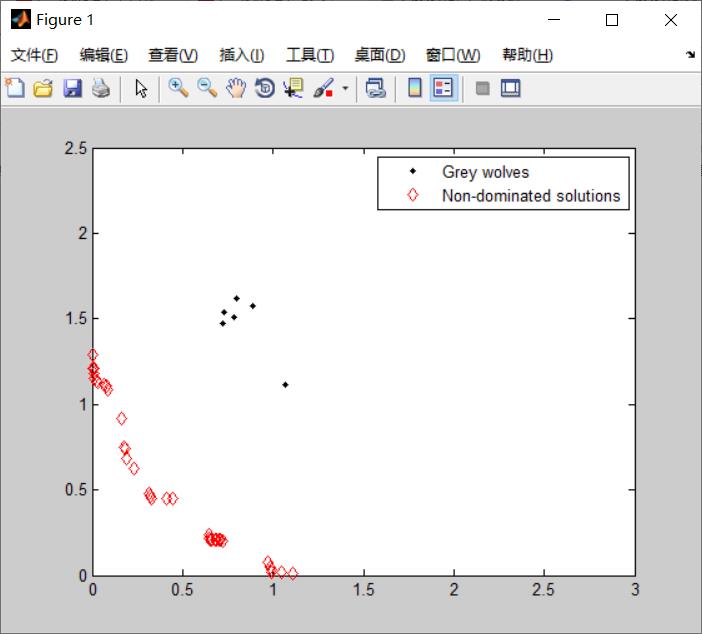

    完整代码或者代写添加QQ1575304183

以上是关于优化求解多目标灰狼优化算法MOGWOmatlab源码的主要内容，如果未能解决你的问题，请参考以下文章

多目标优化求解基于matlab非支配排序灰狼优化（NS-GWO）算法求解多目标优化问题含Matlab源码 2015期

优化求解改进灰狼算法求解重油热解模型matlab源码

优化求解改进灰狼算法求解重油热解模型matlab源码

单目标优化求解基于matlab贪婪非分级灰狼算法求解单目标优化问题（G-NHGWO）含Matlab源码 2005期

matlab改进灰狼算法求解路径优化

matlab改进灰狼算法求解路径优化