优化求解改进灰狼算法求解重油热解模型matlab源码
Posted 博主QQ2449341593
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了优化求解改进灰狼算法求解重油热解模型matlab源码相关的知识,希望对你有一定的参考价值。
一、简介
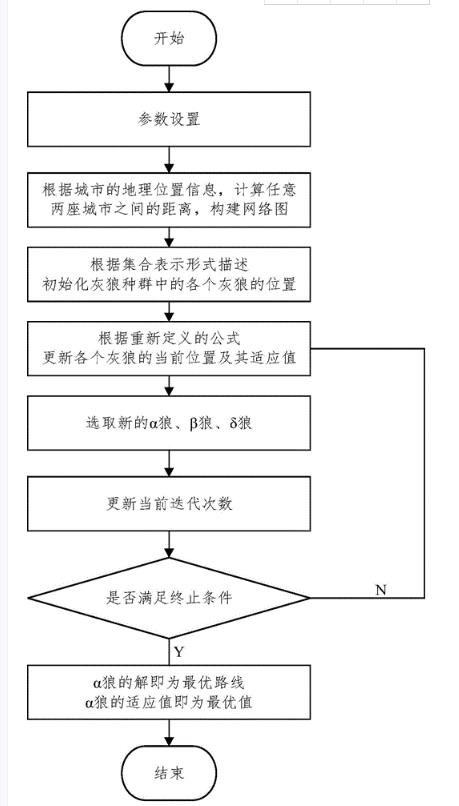
本文提供的一种基于多目标的改进灰狼优化算法,包括:
S1、设置狼群的初始化参数及方向修正概率,在解空间中随机初始化每个狼个体的位置;
S2、根据求解目标计算每个狼个体的适应度值,并选择排名靠前的三只狼个体依次赋予Xα、Xβ、Xδ;
S3、根据Xα、Xβ、Xδ优化狼群每个狼个体的位置,产生中庸狼,并计算中庸狼的适应度值和更新狼群位置;
S4、对更新后的狼群执行方向修正操作并根据方向修正概率控制更新后的狼群参与修正维的规模,产生新的中庸狼,并计算新的中庸狼的适应度值,获得修正后的狼群位置;
S5、判断迭代次数是否达到预设最大迭代次数,若是,则输出修正后的狼群位置作为最终优化结果,否则,转至S3继续进行迭代搜索。
可选地,S1具体包括:
设置狼群的大小M、最大迭代次数max gen及方向修正概率pv,在解空间中随机初始化每个狼个体的位置。
可选地,S2具体包括:
根据求解目标计算每个狼个体的适应度值,并依据快速非劣解排序操作、拥挤距离计算、精英保留策略选择排名靠前的三只狼个体依次赋予Xα、Xβ、Xδ。
可选地,快速非劣解排序操作具体包括:
找到狼群中的非支配解集,将非支配解集标记为第一非支配层F1并将非支配解集中的所有狼个体赋予第一非支配序值,并将所有狼个体剔除;
在剔除后的狼群中找出下一层非支配解集并进行标记、非支配序值赋予操作及剔除操作;
依次持续进行对狼群进行非支配解集分层、标记、非支配序值赋予操作及剔除操作,直至整个狼群被完全分层并使得同一非支配层内的狼个体具有相同的非支配序值。
可选地,拥挤距离计算具体包括:
初始化同一非支配层内的狼个体的距离,令狼个体i的拥挤距离L[i]d为0;
同一非支配层内的狼个体按第m个目标值进行递增排序;
给定边缘上的两只狼个体赋予一个大数Inf,使两只狼个体具有绝对选择优势;
对排序中间的狼个体根据公式八求排序中间的狼个体的拥挤距离,公式八具体为:
其中,Nobj为目标数,分别为第i+1和第i-1只狼个体的第m个适应度值,分别为非劣解集中第m个适应度值的最大值和最小值。
可选地,S3具体包括:
根据Xα、Xβ、Xδ通过狼群包围和狼群猎捕的步骤优化狼群每个狼个体的位置,产生中庸狼,并计算中庸狼的适应度值和依据快速非劣解排序操作、拥挤距离计算、精英保留策略选择性更新狼群位置。
可选地,S3与S4之间还包括:
对更新后的狼群的所有狼个体的每一维通过公式九执行归一化操作,公式九具体为:
其中,D为维数,为狼的第d维变量,为归一化后所对应的标量,max(d)、min(d)分别为狼群中第d维变量的上下限。
可选地,S4具体包括:
对更新后的狼群执行方向修正操作并根据方向修正概率控制更新后的狼群参与修正维的规模,产生新的中庸狼,并计算新的中庸狼的适应度值,根据快速非劣解排序操作、拥挤距离计算、精英保留策略择优保留狼个体位置,并根据狼群中的狼个体排名,将狼群划分为Xα、Xβ、Xδ、Xω,获得修正后的狼群位置。
可选地,对更新后的狼群执行方向修正操作具体包括:
通过公式十对更新后的狼群执行方向修正操作,公式十具体为:
其中,d1,d2∈(1,D),r为0到1的随机数,为中庸狼个体标量的第d1维;
对产生的中庸狼个体标量的每一维通过公式十一进行反归一化操作,公式十一具体为:
其中,为中庸狼的第d维。
可选地,S5具体包括:
判断迭代次数是否达到预设最大迭代次数,若是,则输出修正后的狼群位置作为最终优化结果,并结合模糊决策方法选择最优折中解,否则,转至S3继续进行迭代搜索。
从以上技术方案可以看出,本发明实施例具有以下优点:
本例提供了一种基于多目标的改进灰狼优化算法,包括:S1、设置狼群的初始化参数及方向修正概率,在解空间中随机初始化每个狼个体的位置;S2、根据求解目标计算每个狼个体的适应度值,并选择排名靠前的三只狼个体依次赋予Xα、Xβ、Xδ;S3、根据Xα、Xβ、Xδ优化狼群每个狼个体的位置,产生中庸狼,并计算中庸狼的适应度值和更新狼群位置;S4、对更新后的狼群执行方向修正操作并根据方向修正概率控制更新后的狼群参与修正维的规模,产生新的中庸狼,并计算新的中庸狼的适应度值,获得修正后的狼群位置;S5、判断迭代次数是否达到预设最大迭代次数,若是,则输出修正后的狼群位置作为最终优化结果,否则,转至S3继续进行迭代搜索。本发明实施例中通过利用纵横交叉算法中纵向交叉操作处理部分维容易陷入局部最优问题的独有优势,在标准灰狼算法基础上,融入方向修正操作(纵向交叉操作),提供一种新的狼群位置更新方法,以帮助部分陷入局部最优的维摆脱当前困局,修正狼群的前进方向,增强算法的全局收敛性,解决了现有技术中的标准灰狼算法在处理多目标优化问题时存在着收敛速度慢、容易陷入局部最优值等缺陷的技术问题。
-
%__________________________________________ clear all clc for t = 1:1 SearchAgents_no=30; % Number of search agents Max_iteration=100; % Maximum numbef of iterations % Load details of the selected benchmark function % [lb,ub,dim,fobj]=Get_Functions_details(Function_name); fobj = @heavyoilevaluate; ub = [10,10,10,1500,4000,4500,5,5]; lb = [0,0,0,800,1500,1500,0,0]; dim = size(ub,2); [Best_score,Best_pos,GWO_cg_curve]=GWO(SearchAgents_no,Max_iteration,ub,lb,dim,fobj); display(['The best solution obtained by GWO is : ', num2str(Best_pos)]); display(['Best value by GWO is : ', num2str(Best_score)]); end opt=heavyoilevaluate(Best_pos,20); %重油热解模型 陶毕业论文第7章 function opt=heavyoilevaluate(input,select) B=0; Klp0=input(1);%范围(0,10) Kwp0=input(2);%(0,10) Kwlp0=input(3);%(0,10) Elp=input(4);%(800,1500) Ewp=input(5);%(1500,4000) Ewlp=input(6);%(1500,4500) nl=input(7);%(0,5) nw=input(8);%(0,5) if select == 20 T=[673,683,693,703,698,713,723,733,663,708,703,689,725,715,695,663,683,703,713,723];%自变量 X=[0.3122,0.3348,0.405,0.4034,0.2674,0.4514,0.51,0.574,0.1739,0.4719,0.3478, 0.3562,0.5918,0.4075,0.3355,0.1893,0.222,0.3927,0.3306,0.342]; XL0=[0.2034,0.2305,0.3041,0.3209,0.1638,0.3282,0.3555,0.3685,0.1064,0.3222,0.2346,0.2609,0.4101,0.2724,0.2369,0.1104,0.1447,0.3049,0.2426,0.2559]; end if select == 56 T=[ 673 723 673 723 673 673 683 683 683 703 683 683 693 683 695 698 703 723 708 713 698 713 713 733 708 733 713 713 715 733 723 733 725 663 733 663 708 673 689 673 693 673 693 683 684 683 703 693 703 703 708 713 713 723 719 723]; X = [ 0.3122 0.4371 0.3138 0.3637 0.3879 0.2075 0.3348 0.3110 0.3384 0.3927 0.4684 0.2220 0.4050 0.2599 0.3355 0.2846 0.4034 0.3420 0.4266 0.3306 0.2674 0.2062 0.4514 0.4585 0.4534 0.4720 0.4552 0.4447 0.4075 0.3729 0.5100 0.4234 0.5918 0.1739 0.5740 0.1893 0.3637 0.2169 0.3562 0.1619 0.3397 0.0649 0.2381 0.2512 0.3031 0.1410 0.5436 0.2532 0.3478 0.3973 0.4719 0.4162 0.4232 0.4203 0.5367 0.3011]; XL0 = [ 0.2034 0.2802 0.2136 0.2674 0.2806 0.1282 0.2305 0.2276 0.2497 0.3049 0.3693 0.1447 0.3041 0.1822 0.2369 0.2045 0.3209 0.2559 0.3107 0.2426 0.1638 0.1397 0.3326 0.2977 0.3260 0.3099 0.3282 0.3441 0.2724 0.2688 0.3555 0.3083 0.4101 0.1064 0.3685 0.1104 0.2449 0.1541 0.2609 0.1103 0.2482 0.0439 0.1483 0.1867 0.1976 0.0983 0.3831 0.1833 0.2346 0.3018 0.3222 0.3266 0.2945 0.3390 0.3354 0.2510]'; end N = max(size(XL0)); for k=1:1:N temp1=Klp0*exp(-Elp/T(k))/nl*(1-(1-X(k))^nl); temp2=Kwp0*Kwlp0*exp(-(Ewp+Ewlp)/T(k))/(nw-Kwlp0*exp(-Ewlp/T(k))); temp3=(1-(1-X(k))^(Kwlp0*exp(-Ewlp/T(k))))/(Kwlp0*exp(-Ewlp/T(k))); temp4=((1-X(k))^nw-1)/nw; XXL(k)=temp1+temp2*(temp3+temp4);%模型输出 B=B+abs(XL0(k)-XXL(k));%目标函数值 end if size(input,1) <= 1 subplot(2,1,1) t = 1:1:N; plot(t,XL0,'-k','linewidth',1.5); hold on plot(t,XXL,'--b','linewidth',1.5); hold off xlabel('sample point','fontsize',9); ylabel('output','fontsize',9); legend('actual output','estimate output'); set(legend,'fontname','Times New Roman') set(legend,'fontsize',9) subplot(2,1,2) plot(t,XL0 -XXL,'-.g','linewidth',1.5) hold off xlabel('sample point','fontsize',9); ylabel('output','fontsize',9); legend('output error'); set(legend,'fontname','Times New Roman') set(legend,'fontsize',9) data = [XL0',XXL'] end opt=B;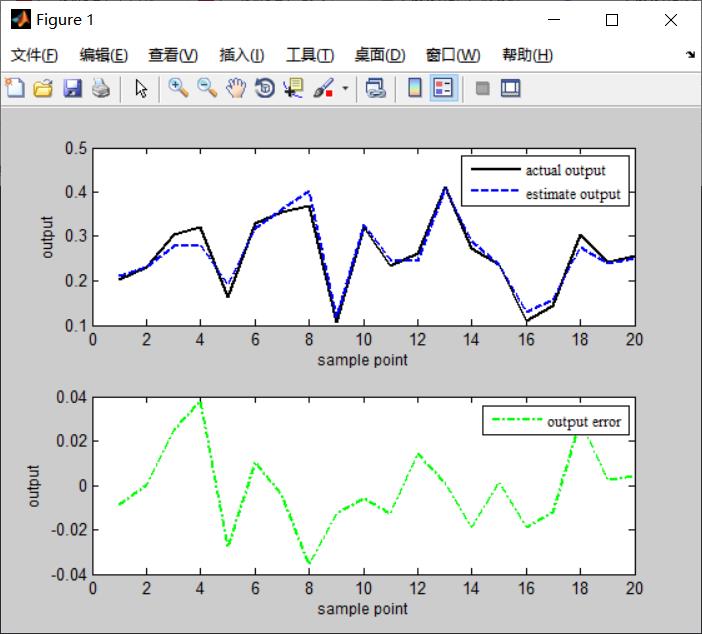
以上是关于优化求解改进灰狼算法求解重油热解模型matlab源码的主要内容,如果未能解决你的问题,请参考以下文章