JZ1.二维数组中的查找；JZ4. 重建二叉树；JZ7. 斐波那契数列；JZ.13 调整数组顺序使奇数位于偶数前；JZ19. 顺序打印矩阵

Posted 2021-05-18 小猪媛不圆

剑指Offer——数组

• JZ1.二维数组中的查找
• JZ4. 重建二叉树
• JZ7. 斐波那契数列
• JZ.13 调整数组顺序使奇数位于偶数前
• JZ19. 顺序打印矩阵

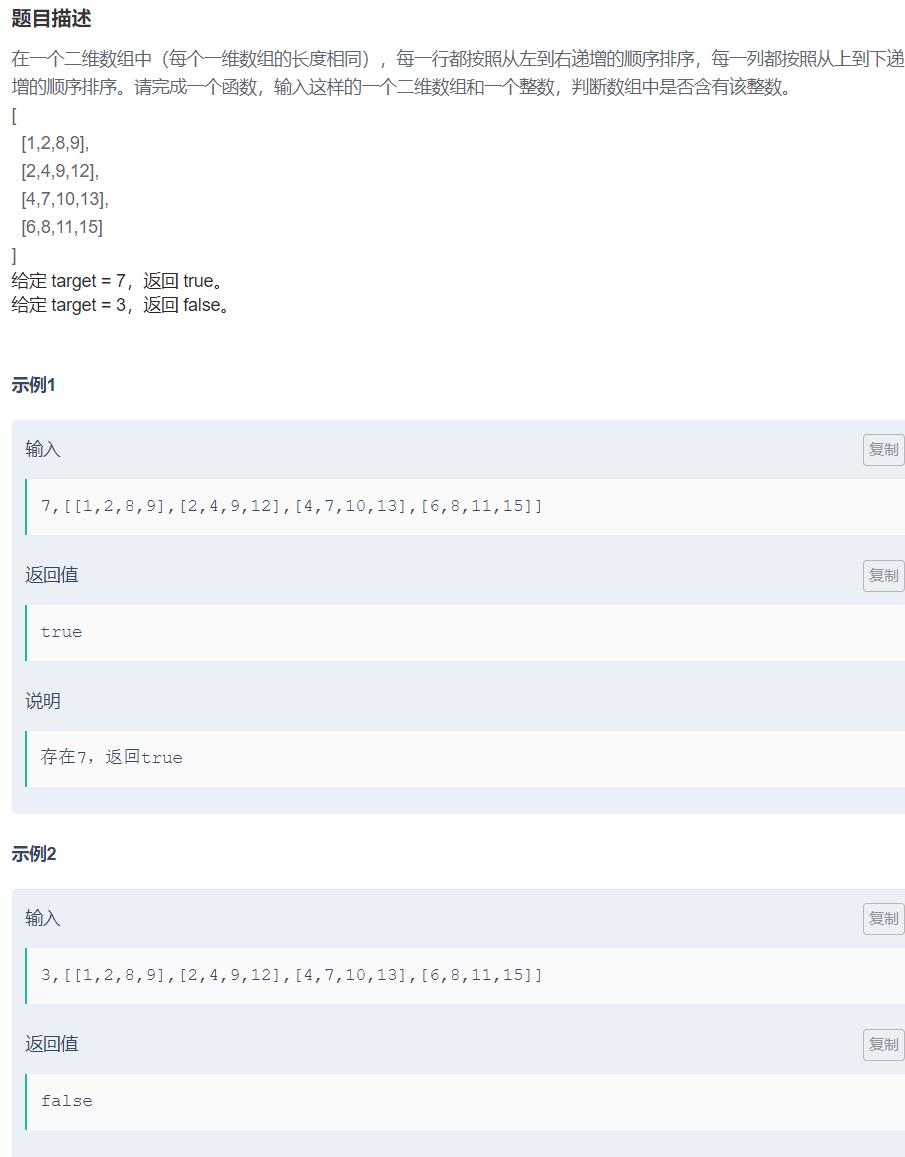
JZ1.二维数组中的查找

题目链接

• 程序代码

public class Solution {
    public boolean Find(int target, int [][] array) {
        int rows = array.length;
        if(rows == 0)return false;
        int cols = array[0].length;
        if(cols == 0) return false;
        int row = 0;
        int col = cols-1;
        while(row < rows && col >= 0) {
            if(array[row][col] < target) {
                row++;
            } else if(array[row][col] > target) {
                col--;
            } else {
                return true;
            }
        }
        return false;
    }
}

• 简单描述

这里可以使用两层for循环，但是效率不是很高，所以我们选择这种方式

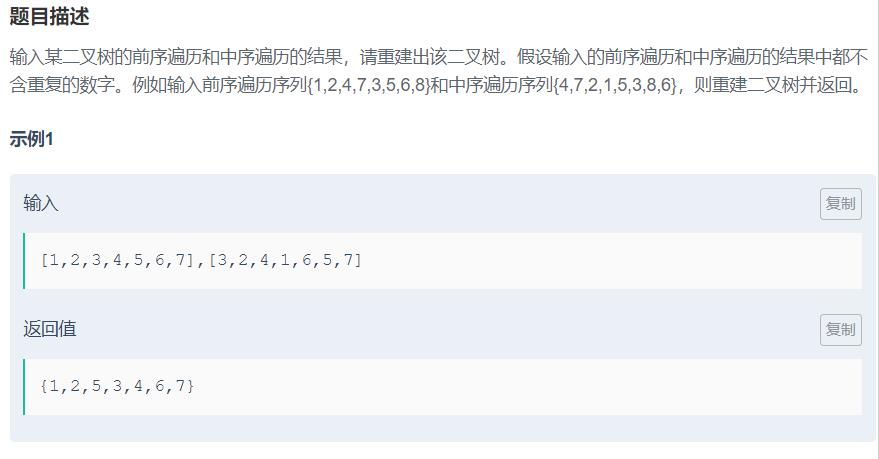
JZ4. 重建二叉树

题目链接

• 程序代码

/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
import java.util.*;
public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        if(pre.length == 0 || in.length == 0) {
            return null;
        }
        TreeNode root = new TreeNode(pre[0]);
        //在中序中找到前序的根
        for(int i = 0; i < in.length; i++) {
            if(in[i] == pre[0]){
                //左子树
                root.left = reConstructBinaryTree(Arrays.copyOfRange(pre,1,i+1),Arrays.copyOfRange(in,0,i));
                //右子树
                root.right = reConstructBinaryTree(Arrays.copyOfRange(pre,i+1,pre.length),Arrays.copyOfRange(in,i+1,in.length));
                break;
            }
        }
        return root;
    }
}

• 简要描述

根据中序遍历和前序遍历可以确定二叉树，具体过程为：
①根据前序序列第一个结点确定根结点
②根据根结点在中序序列中的位置分割出左右两个子序列
③对左子树和右子树分别递归使用同样的方法继续分解
例如：
前序序列{1,2,4,7,3,5,6,8} = pre
中序序列{4,7,2,1,5,3,8,6} = in
根据当前前序序列的第一个结点确定根结点，为 1
找到 1 在中序遍历序列中的位置，为 in[3]
切割左右子树，则 in[3] 前面的为左子树， in[3] 后面的为右子树
则切割后的左子树前序序列为：{2,4,7}，切割后的左子树中序序列为：{4,7,2}；切割后的右子树前序序列为：{3,5,6,8}，切割后的右子树中序序列为：{5,3,8,6}
对子树分别使用同样的方法分解

JZ7. 斐波那契数列

题目链接

• 程序代码

public class Solution {
    public int Fibonacci(int n) {
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;
        return Fibonacci(n-1) + Fibonacci(n-2);
    }
}

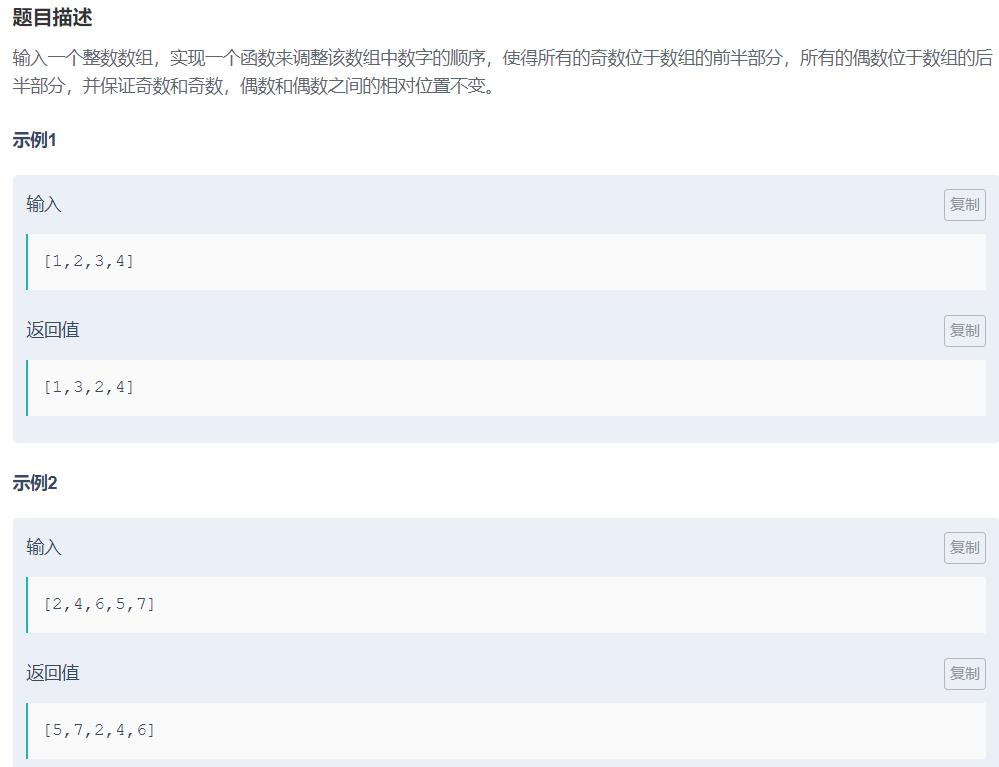
JZ.13 调整数组顺序使奇数位于偶数前

题目链接

• 程序代码

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param array int整型一维数组 
     * @return int整型一维数组
     */
    public int[] reOrderArray (int[] array) {
        // write code here
        if(array.length == 0) return array;
        Queue<Integer> jishu = new LinkedList<>();
        Queue<Integer> oushu = new LinkedList<>();
        for(int i = 0; i < array.length; i++) {
            if(array[i] % 2 != 0) {
                jishu.add(array[i]);
            } else {
                oushu.add(array[i]);
            }
        }
        for(int i = 0; i < array.length; i++) {
            if(! jishu.isEmpty()) {
                array[i] = jishu.poll();
            } else {
                array[i] = oushu.poll();
            }
        }
        return array;
    }
}

• 简单描述

这里参考了牛客上一个博主的解答~
思路：开辟两组新的空间，这里用的是LinkedList，因为想要用到队列的先进先出方法
1.先找出奇数利用3余某个数不为0就是奇数（不考虑0的情况），那么余2是0的就是偶数
2.然后奇数放在一个立案表里，偶数放在一个链表里。链表不需要事先知道长度大小，所以用链表方便。数组是没有办法确定大小的
3.就先将放了奇数的链表一个一个出栈（poll函数）放在题目给的array中，然后就是偶数

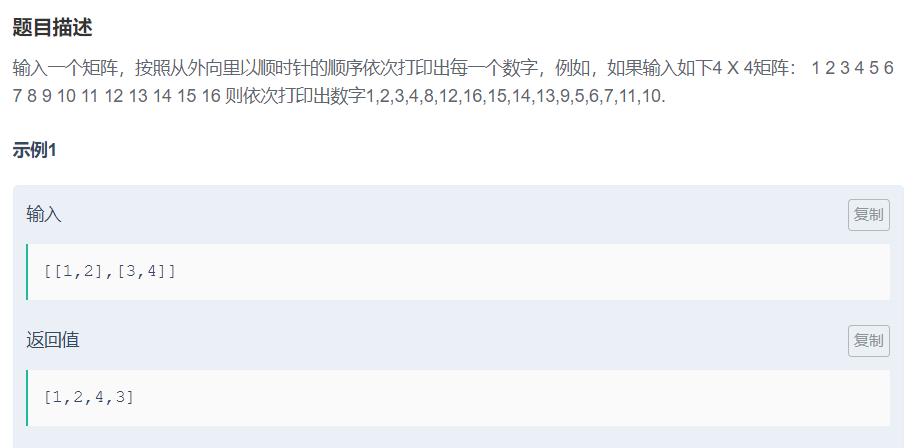
JZ19. 顺序打印矩阵

题目链接

• 程序代码

import java.util.ArrayList;
public class Solution {
    public ArrayList<Integer> printMatrix(int [][] matrix) {
       ArrayList<Integer> list = new ArrayList<>();
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return list;
        }
        int up = 0;
        int down = matrix.length - 1;
        int left = 0;
        int right = matrix[0].length - 1;
        while(true) {
            for(int col = left;col <= right; col++) {
                list.add(matrix[up][col]);
            }
            up++;
            if(up > down) {
                break;
            }
            for(int row = up; row <= down ; row++) {
                list.add(matrix[row][right]);
            }
            right--;
            if(left > right) {
                break;
            }
            for(int col = right;col >= left; col--) {
                list.add(matrix[down][col]);
            }
            down--;
            if(up > down) {
                break;
            }
            for(int row = down; row >= up; row--) {
                list.add(matrix[row][left]);
            }
            left ++;
            if(left > right) {
                break;
            }
        }
        return list;
    }
}

• 简单描述

参考牛客上一个博主的题解~
定义四个变量代表范围：up,down,left,right
1.向右走存入整行的值，当存入后，该行再也不会被遍历，代表上边界的up加一，同时判断是否和代表下边界的down交错
2.向下走存入整列的值，当存入后，该列再也不会被遍历，代表有边界的right减一，同时判断是否和左边界的left交错
3.向左走存入整行的值，当存入后，该行再也不会被遍历，代表下边界的down减一，同时判断是否和上边界up交错
4.向上走存入整列的值，当存入后，该列再也不会被遍历，代表左边界的left加一，同时哦按段是否和代表有边界的right交错