P3834 模板可持久化线段树 2（整体二分做法）

Posted 2021-05-16 Jozky86

P3834 【模板】可持久化线段树 2（主席树）

我们详细讲讲这个整体二分如何求区间第k小
我们都知道二分可以求出区间里某个想要的值，如果有很多询问，我们对每个询问都进行二分，复杂度就是O(QNlog(1e9))铁超，那怎么优化呢？
我们先看第一个图
对于7个数的区间[1,5,2,6,3,7,4]，我们有两个询问，[2,5]的第3小，[4,4]的第1小
我们先对区间[2,5]进行二分，会得到：
[1,7] mid=4 n=2<3,(这里3是我们要求的第3小数，2指的是区间[2,5]内<=mid的数量)
[5,7] mid=6 n=4>=3(以下同里)
[5,6] mid=5 n=3 >=3
[5,5]->（l == r）ans = 5
然后我们对区间[4,4]二分，也会得到差不多的过程：
[1,7] mid=4 n=0<1
[5,7] mid=6 n=1>=1
[5,6] mid=5 n=0<1
[6,6]–>ans=6
我们刚才说过对于每个区间二分是不行的，因为会超时，现在我们对这两个过程进行对比，发现有大量过程是在同一个而区间进行的，都会到[1,7],[5,7],[5,6]这三个区间，所以整体二分的含义就是将所有区间当作一个整体二分。

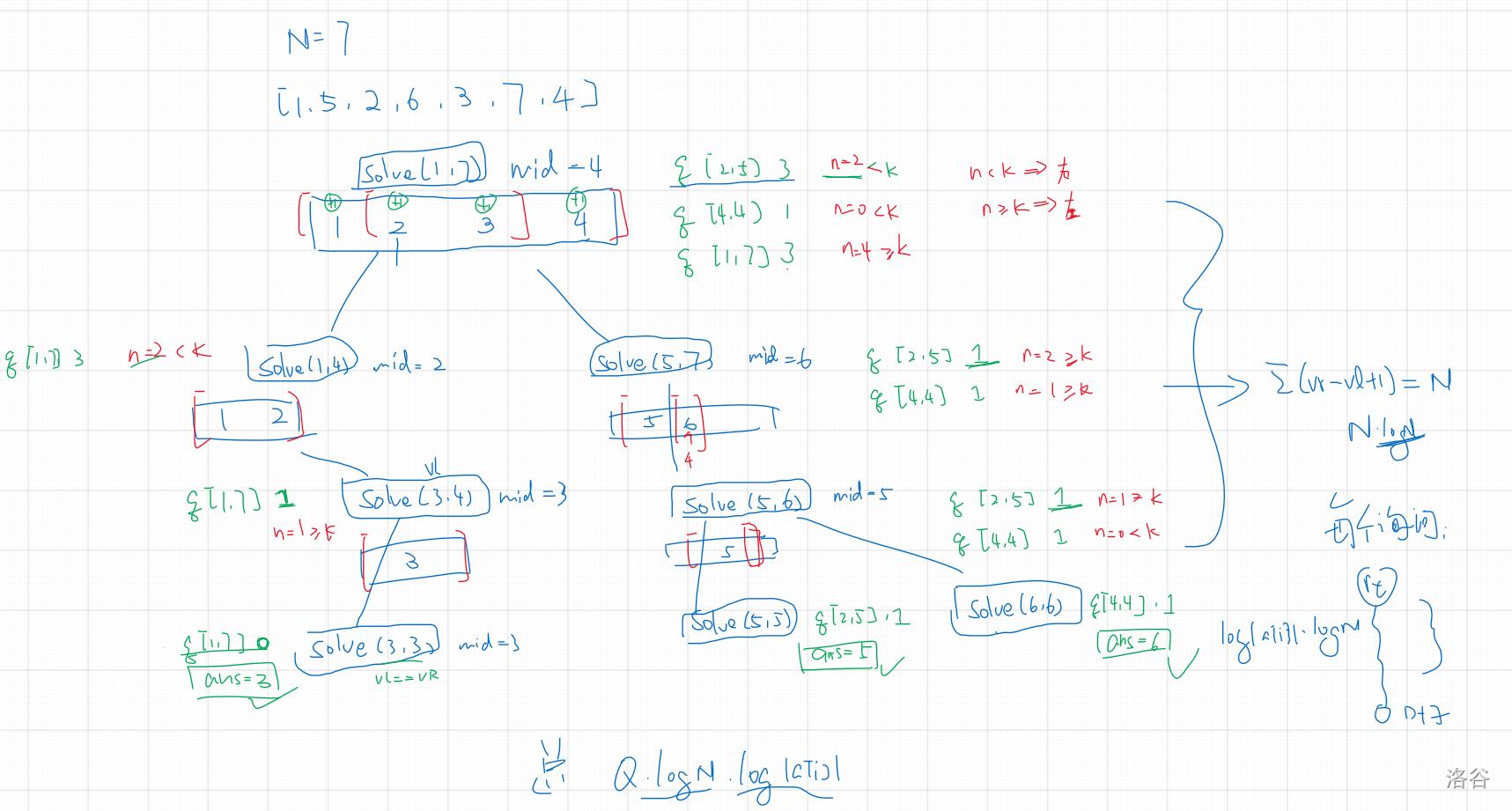
现在看图2：
数组[1,5，2，6，3，7，4]
我们现在要进行三次查询，分别是：
[2,5] 3
[4,4] 1
[1,7] 3
我们现在开始模拟过程：
一开始二分区间[1,7] mid=4
[2,5] K=3 n=2<K
[4,4] K=1 n=0<K
[1,7] K=3 n=4>=K
n<mid的向右继续寻找，n>=mid向右寻找
[1,7] K=3就向左找，此时寻找区间就变成[1,4] mid=2 ,此时n=2<K,向右找，一直到区间左右一样
[2,5]和[4,4]向右找，向右找时K是要减去n的，相当于左边已经有n个小于K的值，我们去右边只需要找第K-n的值就可以了
此时区间为[5,7]mid=6
[2,5] K=1 n=2>=K
[4,4] K=1 n=1>=K
继续上述过程
最终会形成一个类似树的结构，看看图就知道了，这样复杂度就优化了
n的计算要用得到树状数组
复杂度为：O(QlogNlog(1e9))
logN为树状数组，log(1e9)为二分

代码中的lq和rq数组就是将在每次二分中，将询问区间分成两部分，就如图2中将
[2,5] K=3 n=2<K
[4,4] K=1 n=0<K
[1,7] K=3 n=4>=K
这三个操作，将前两个分为一组，第三个分为另一组

代码：

#pragma optimize("Ofast")
#include<bits/stdc++.h>
#define MAXN 400005
#define inf int(1e9)
using namespace std;
typedef long long ll;

int N,M;
struct Node{
    int op,x,y,k;//op=insert+1/remove-1,query2
    int id;
    Node(int op=0, int x=0, int y=0, int k=0, int id=0):op(op), x(x), y(y), k(k), id(id){}
} q[MAXN],lq[MAXN],rq[MAXN];

//
int fw[MAXN];
inline int lbt(int x){
    return x&(-x);
}

inline void change(int x, int dv){
    for(;x<=N;x+=lbt(x)){
        fw[x] += dv;
    }
}

inline int query(int x){
    int ans = 0;
    for(;x>0;x-=lbt(x)){
        ans += fw[x];
    }
    return ans;
}
//
int ANS[MAXN];

void solve(int vl, int vr, int ql, int qr){
    //cerr<<"solve: "<<vl<<" "<<vr<<" "<<ql<<" "<<qr<<endl;
    if(ql > qr) return;
    if(vl == vr){
        for(int i=ql;i<=qr;i++){
            if(q[i].op==2) ANS[q[i].id] = vl;
        }
        return;
    }
    //insert
    int mid = (vl + vr)>>1;
    int nl = 0, nr = 0;
    for(int i=ql;i<=qr;i++){
        if(q[i].op != 2){//insert/remove
            if(q[i].x <= mid) change(q[i].y, q[i].op), lq[++nl] = q[i];
            else rq[++nr] = q[i];
        }
        else{//query
            int n = query(q[i].y) - query(q[i].x-1);
            if(q[i].k <= n) lq[++nl] = q[i];
            else{
                q[i].k -= n;
                rq[++nr] = q[i];
            }
        }
    }

    //remove
    for(int i=ql;i<=qr;i++){
        if(q[i].op != 2){
            if(q[i].x <= mid) change(q[i].y, -q[i].op);
        }
    }

    for(int i=1;i<=nl;i++) q[ql+i-1] = lq[i];
    for(int i=1;i<=nr;i++) q[ql+nl+i-1] = rq[i];
    solve(vl, mid, ql, ql+nl-1);
    solve(mid+1, vr, ql+nl, qr);
}

int main(){
    scanf("%d%d", &N, &M);
    int x,l,r,k;;
    for(int i=1;i<=N;++i){
        scanf("%d", &x);
        q[i] = Node(1,x,i);
    }
    for(int i=1;i<=M;i++){
        scanf("%d%d%d", &l, &r, &k);
        q[N+i] = Node(2,l,r,k,i);
    }

    solve(-1e9,1e9,1,N+M);
    for(int i=1;i<=M;i++){
        printf("%d\\n", ANS[i]);
    }
    return 0;
}