leetcode 99. 恢复二叉搜索树
Posted 大忽悠爱忽悠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了leetcode 99. 恢复二叉搜索树相关的知识,希望对你有一定的参考价值。
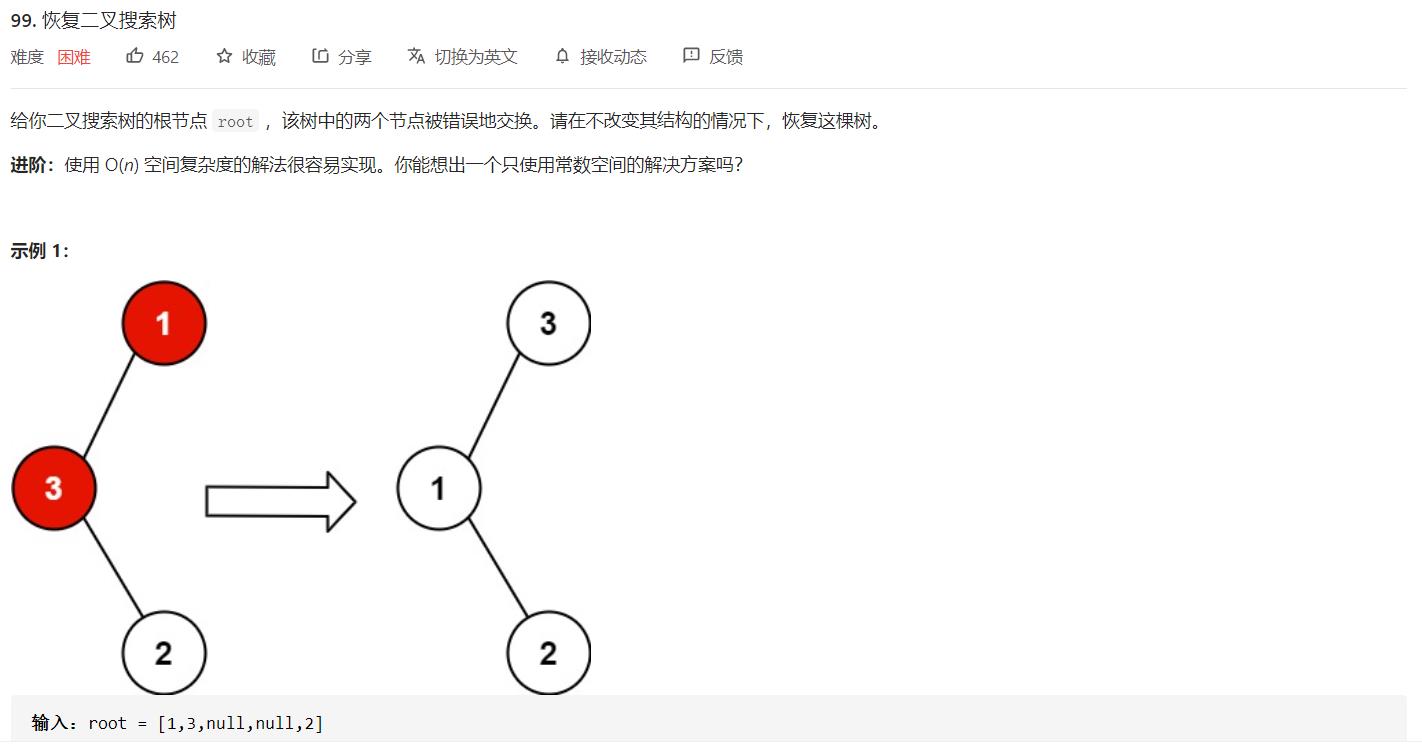
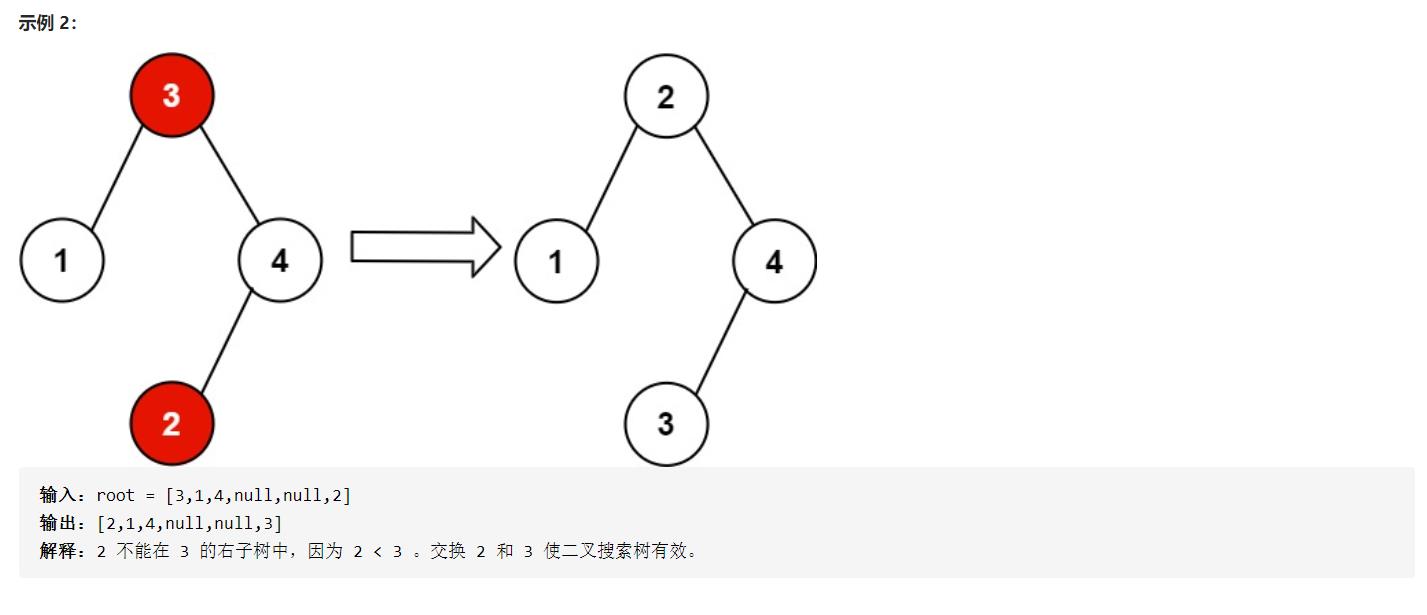
解题方法汇总如下
1.递归法
思路:
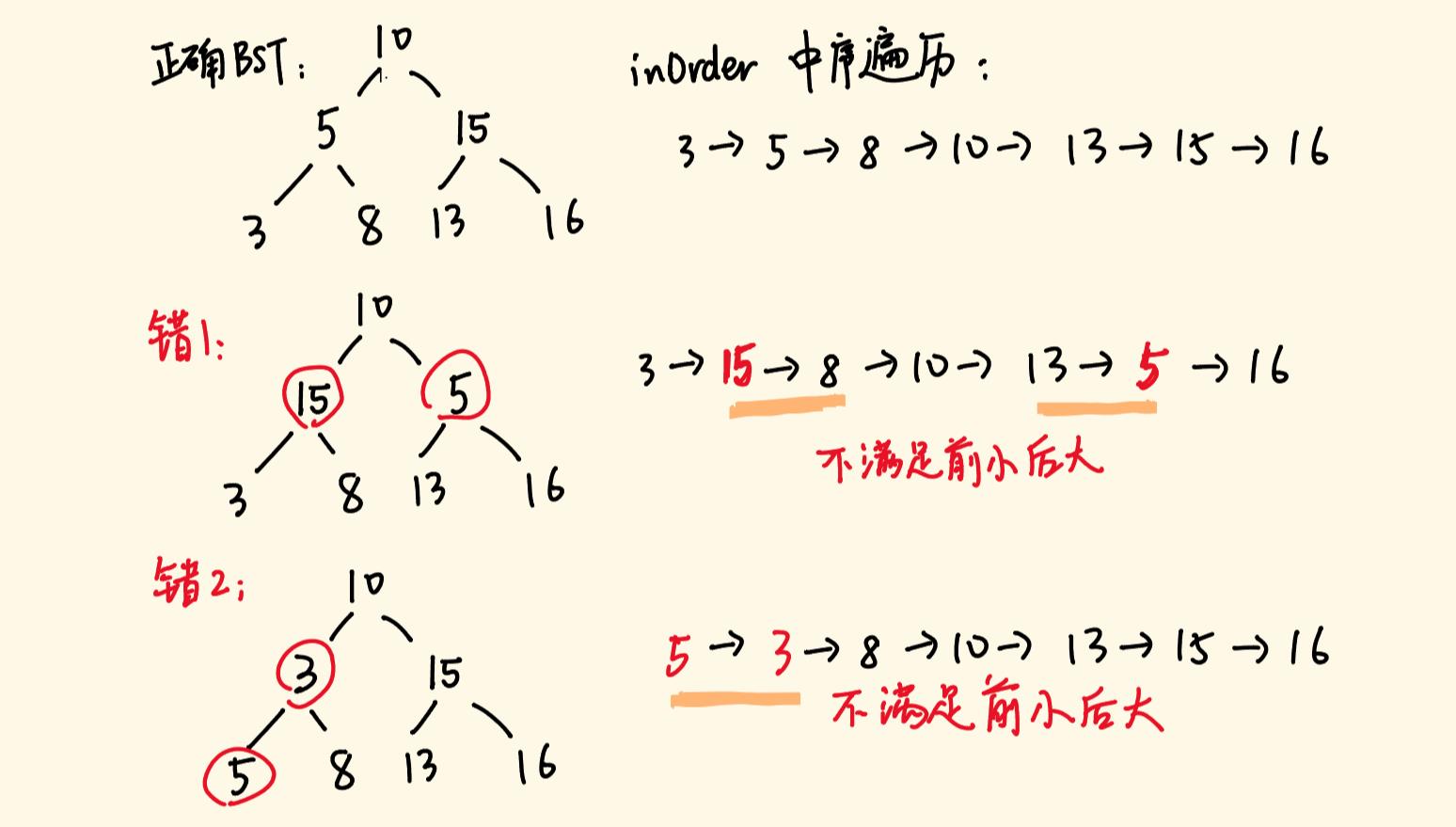
中序遍历BST,依次访问的节点值是递增的,错误的BST会破坏递增性,从而能定位出错误。
我发现,错误有两种:
- 错误1:出现了两对不满足前小后大,需要交换第一对的第一个元素与第二对的第二个元素。
- 错误2:只出现一对不满足前小后大,交换这一对元素即可。
- 比较前后访问的节点值,prev 保存上一个访问的节点,当前访问的是 root 节点。
- 每访问一个节点,如果prev.val>=root.val,就找到了一对“错误对”。
- 检查一下它是第一对错误对,还是第二对错误对。
- 遍历结束,就确定了待交换的两个错误点,进行交换。
特别注意:如果是错误1,交换第一对的第一个元素与第二对的第二个元素
代码:
class Solution {
public:
TreeNode* prev=NULL,*p1=NULL,*p2=NULL;
void recoverTree(TreeNode* root)
{
if (root == NULL)
return;
//这里prev初始默认为最小值
prev = new TreeNode(INT_MIN);
travle(root);
swap(p1->val, p2->val);
}
void travle(TreeNode* root)
{
if (!root) return;
travle(root->left);
if (prev->val > root->val && p1 == NULL)// 当前是第一对错误
p1 = prev; // 记录第一个错误点
if (prev->val > root->val && p1 != NULL)//当前是第二对错误
p2 = root; //记录第二个错误点
//一开始把prev设置成最小值是因为,通过递归最开始处理的是左子树最左下角的叶子节点,
//我们一开始要让该节点赋值给prev,不能让prev满足上面两个条件--取int的最小值
prev = root;// 更新 perv
travle(root->right);
}
};
递归法的第二种写法:
class Solution {
public:
TreeNode* prev=NULL,*p1=NULL,*p2=NULL;
void recoverTree(TreeNode* root)
{
if (root == NULL)
return;
travle(root);
swap(p1->val, p2->val);
}
void travle(TreeNode* root)
{
if (!root) return;
//说明当前节点左子树最下面的叶子节点
if (root->left == NULL && prev == NULL) prev = root;
travle(root->left);
if (prev->val > root->val && p1 == NULL)// 当前是第一对错误
p1 = prev; // 记录第一个错误点
if (prev->val > root->val && p1 != NULL)//当前是第二对错误
p2 = root; //记录第二个错误点
prev = root;// 更新 perv
travle(root->right);
}
};
- 小细节:
if (root->left == NULL && prev == NULL) prev = root; 这里不能直接return 返回 - 举例说明: [2,null,1] 对于当前这颗二叉树来说,当前根节点左孩子为空,右孩子不为空
- 如果写了return,那么刚开始进入循环的时候,进入当前行语句判断时:满足左孩子为空,prev为空的条件,那么直接return退出函数,还没有进行递归操作。 重点是直接忽略了它的右子树
- 因此针对这种情况,return不能写
递归法的第三种写法
class Solution {
public:
TreeNode* prev=NULL,*p1=NULL,*p2=NULL;
int num = 0;// 记录出现的逆序对数
void recoverTree(TreeNode* root)
{
if (root == NULL)
return;
travle(root);
swap(p1->val, p2->val);
}
void travle(TreeNode* root)
{
if (!root) return;
if (num == 2) return;
//这里不能直接return,因为当前节点
if (root->left == NULL && prev == NULL) prev = root;
travle(root->left);
if (prev->val > root->val)
{
if (!p1) p1 = prev;// 出现第二对时, p1就不再赋值
p2 = root;
num++;
}
prev = root;// 更新 perv
travle(root->right);
}
};
- 通过一个变量num来记录出现的逆序对数,当num为2时,表明是错误1,并且num最大值就为2,因为题目说只出现一对错误交换的数字,因此我们可以在num等于二的时候提前斩断递归操作,节约了内存消耗
2.数组法
- 注意题目给出的条件,是 二叉搜索树,这就是意味着节点之间是有顺序关系的。
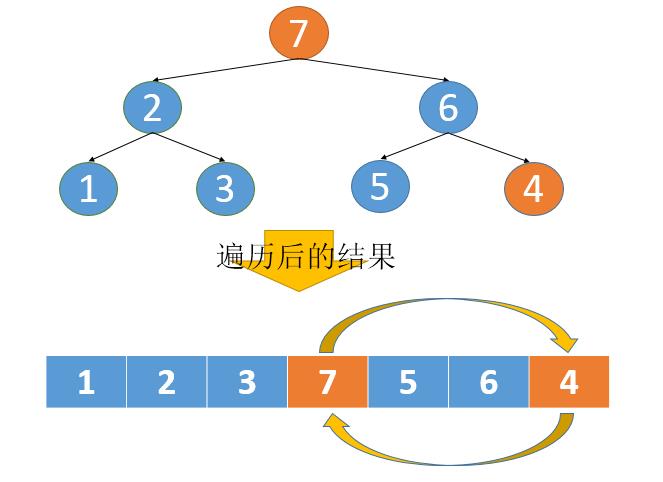
- 如果我们把整棵树都 遍历 一遍,将遍历的结果保存下来,比如放到一个数组中。
- 那么这个数组应该是有序的。
- 既然是有序的那就好办了,我们将这个有序的数组遍历一遍。
- 如果数组是完全有序的,那么直接返回就可以了。
- 否则,我们找到顺序不一致的两个下标i和j,将arr[i].val和arr[j].val的值互换一下即可。
class Solution {
vector<TreeNode*> ret;
public:
void recoverTree(TreeNode* root)
{
if (root == NULL)
return;
dfs(root);
int p1=INT_MIN, p2;//记录需要交换的两个位置下标
//注意:i的终止范围是ret.size()-1,因为这里比较中存在i+1
for (int i = 0; i < ret.size()-1; i++)
{
if (ret[i]->val > ret[i + 1]->val)
{
if (p1 == INT_MIN)
{
p1 = i;
}
p2 = i + 1;
}
}
swap(ret[p1]->val, ret[p2]->val);
}
void dfs(TreeNode* root)
{
if (!root) return;
dfs(root->left);
ret.push_back(root);
dfs(root->right);
}
};
3.mirror遍历
- mirror遍历用到了线索二叉树的思想,在Morris方法中不需要为每个节点额外分配指针指向其前驱(predecessor)和后继节点(successor),只需要利用叶子节点中的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了 。
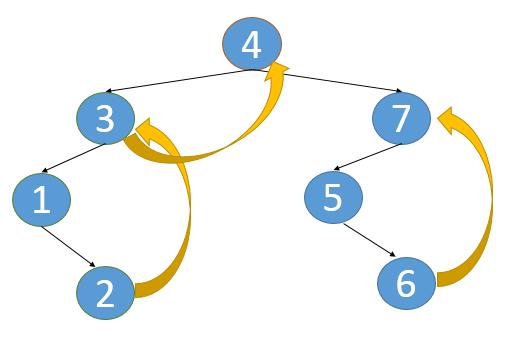
回想一下中序遍历的递归版本是
dfs(root.left)
打印节点 root
dfs(root.right)
- 也就是一路往左走到底,左边走不通了,再往右边走。对于上图来说,就是4->3->1这个过程,一路往左,走不通了再往右,也就是遍历2。
- 当然如果2的右边还有节点那么还会继续遍历下去。
- 现在2的右边已经是空了,对于递归来说操作系统自动出栈,然后会访问3这个节点。
- 既然2是叶子节点,左右子树都是空,我们可以利用这个空闲出来的信息,将2的右子树指向3,这样当2遍历完后,再往右走,就会自动走到3这个节点了。
- 同理,将3的右子树指向4,将6的右子树指向7。
- 这样的话,我们就可以省去额外的栈空间了。利用叶子节点的右子树这个特点,将其重新赋予指向关系 ,就是莫里斯遍历的核心了。
- 不过光是这样还不行,再回看上面那张图,其实已经不是一棵树了,而是变成图了。因为出现了循环。
- 所以,我们还需要将新加这个指向关系给去掉。
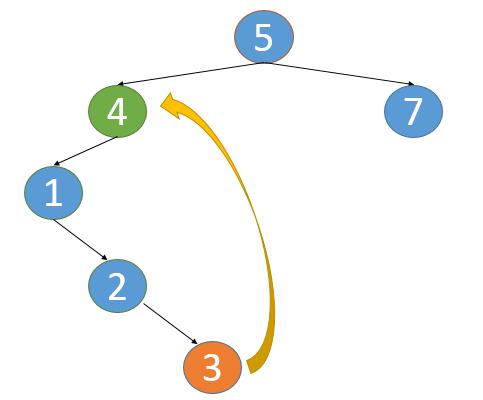
- 对于上图来说,假设我们已经遍历到4 这个节点了,那就意味着4在左子树都遍历完了,对应的就是1,2,3都遍历完了。
- 3.right=4这个是我们新加上的,既然现在已经遍历到4了,我们就可以将3.right=null,将这个指向关系还原即可。
- 从上图中也可以看出,所谓新加的指向关系,就是找到根节点左子树的最右子树,然后将最右子树的right指向根节点。
- 下图完整演示了mirror遍历的过程:
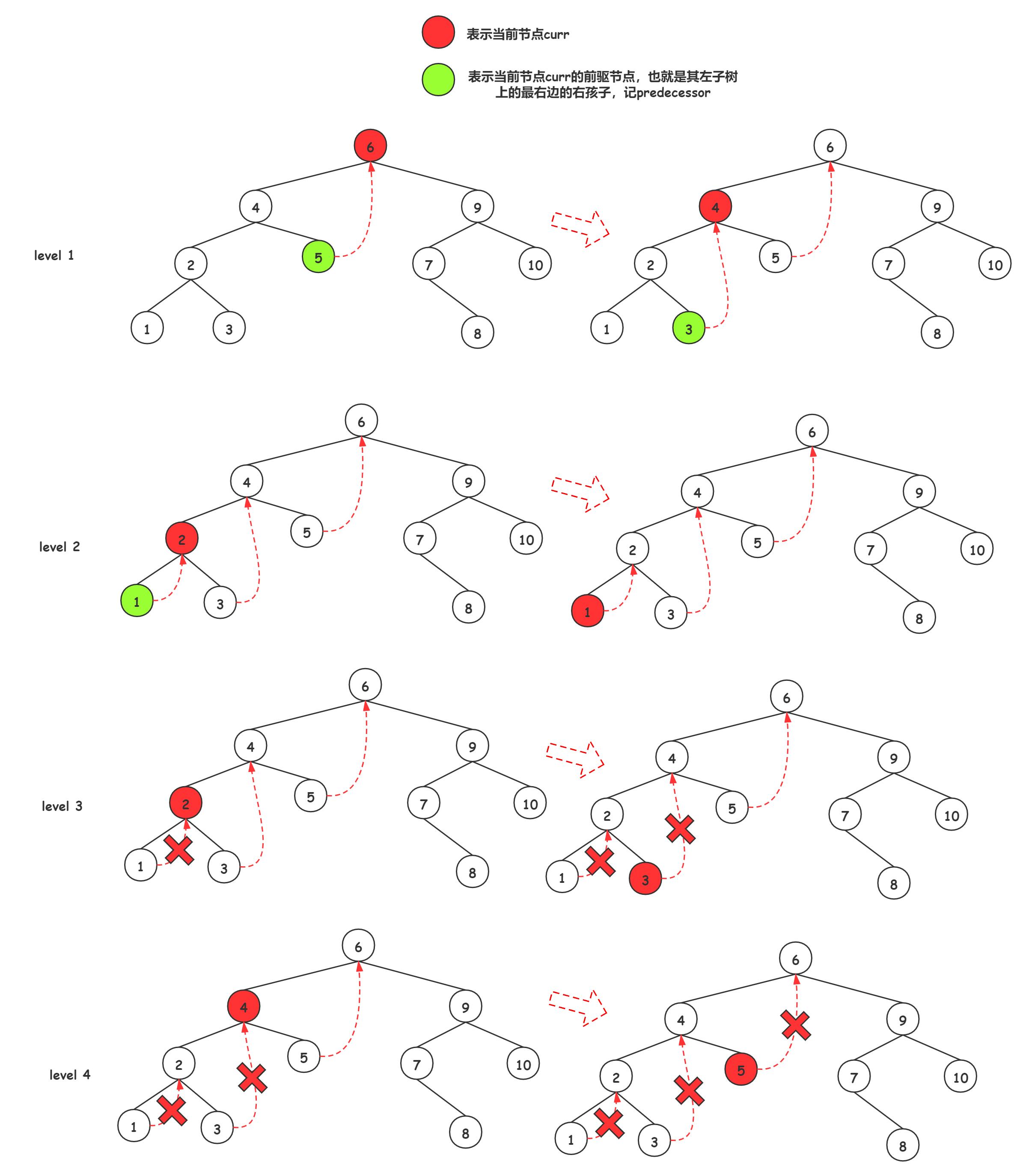
Morris遍历算法的步骤如下: - 检查当前结点的左孩子:
- 如果当前结点的左孩子为空,说明要不没有前驱,要不前驱是它的父结点,所以进行检查,然后进入右孩子。
- 如果当前结点的左孩子不为空,说明左子树里肯定有它的前驱,那就找到这个前驱
- 如果前驱结点的右孩子是空,说明还没检查过左子树,那么把前驱结点的右孩子指向当前结点,然后进入当前结点的左孩子。
- 如果当前结点的前驱结点其右孩子指向了它本身,说明左子树已被检查过,就直接进行检查,然后把前驱结点的右孩子设置为空,恢复原树,再进入右孩子。
Morris代码框架:
while(cur){
if(cur->left == NULL){// 左子树为空时,直接比较,然后进入右子树
/*************
/* 进行你的操作
*************/
pre = cur;
cur = cur->right;
}else{// 进入左子树
/*************
/* 找cur的前驱结点,找到后分两种情况
/* 1、cur的左子结点没有右子结点,那cur的左子结点就是前驱
/* 2、cur的左子结点有右子结点,就一路向右下,走到底就是cur的前驱
*************/
TreeNode* preceesor = cur->left;
while(preceesor->right && preceesor->right != cur){
preceesor = preceesor->right;
}
// 前驱已经指向自己了,直接比较,然后进入右子树
if(preceesor->right == cur){
/*************
/* 进行你的操作
*************/
preceesor->right = NULL; // 断开连接,恢复原树
pre = cur;
cur = cur->right;
}else{ // 前驱还没有指向自己,说明左边还没有遍历,将前驱的右指针指向自己,后进入前驱
preceesor->right = cur;
cur = cur->left;
}
}
}
代码:
class Solution {
public:
// s1 存小索引那个结点,s2存大索引那个结点,pre存前驱结点
TreeNode *s1 = NULL, *s2 = NULL, *pre = NULL;
void recoverTree(TreeNode* root) {
TreeNode* cur = root; // 游标
while(cur != NULL){
if(cur->left != NULL){ // 进入左子树
// 找到cur的前驱结点,分两种情况
// 1、cur的左子结点没有右子结点,那cur的左子结点就是前驱
// 2、cur的左子结点有右子结点,就一路向右下,走到底就是cur的前驱
TreeNode* predecessor = cur->left;
while(predecessor->right != NULL && predecessor->right != cur){
predecessor = predecessor->right;
}
// 前驱还没有指向自己,说明左边还没有遍历,将前驱的右指针指向自己,后进入前驱
if(predecessor->right == NULL){
predecessor->right = cur;
cur = cur->left;
}else{
// 前驱已经指向自己了,直接比较是否有逆序对,然后进入右子树
if(pre != NULL && cur->val < pre->val){
if(s1 == NULL) s1 = pre;
s2 = cur;
}
pre = cur;
predecessor->right = NULL;
cur = cur->right;
}
}else{ // 左子树为空时,检查是否有逆序对,然后进入右子树
if(pre != NULL && cur->val < pre->val){
if(s1 == NULL) s1 = pre;
s2 = cur;
}
pre = cur;
cur = cur->right;
}
}
// 进行交换
int t = s1->val;
s1->val = s2->val;
s2->val = t;
return;
}
};
以上是关于leetcode 99. 恢复二叉搜索树的主要内容,如果未能解决你的问题,请参考以下文章
⭐算法入门⭐《二叉树 - 二叉搜索树》中等09 —— LeetCode 99. 恢复二叉搜索树