leetcode 120. 三角形最小路径和

Posted 2021-05-16 大忽悠爱忽悠

---

三角形最小路径和题解整理

• 递归---超时版本
• 记忆化递归
• 自上而下的动态规划
• 自下而上的动态规划
• 动态规划空间优化

---

递归—超时版本

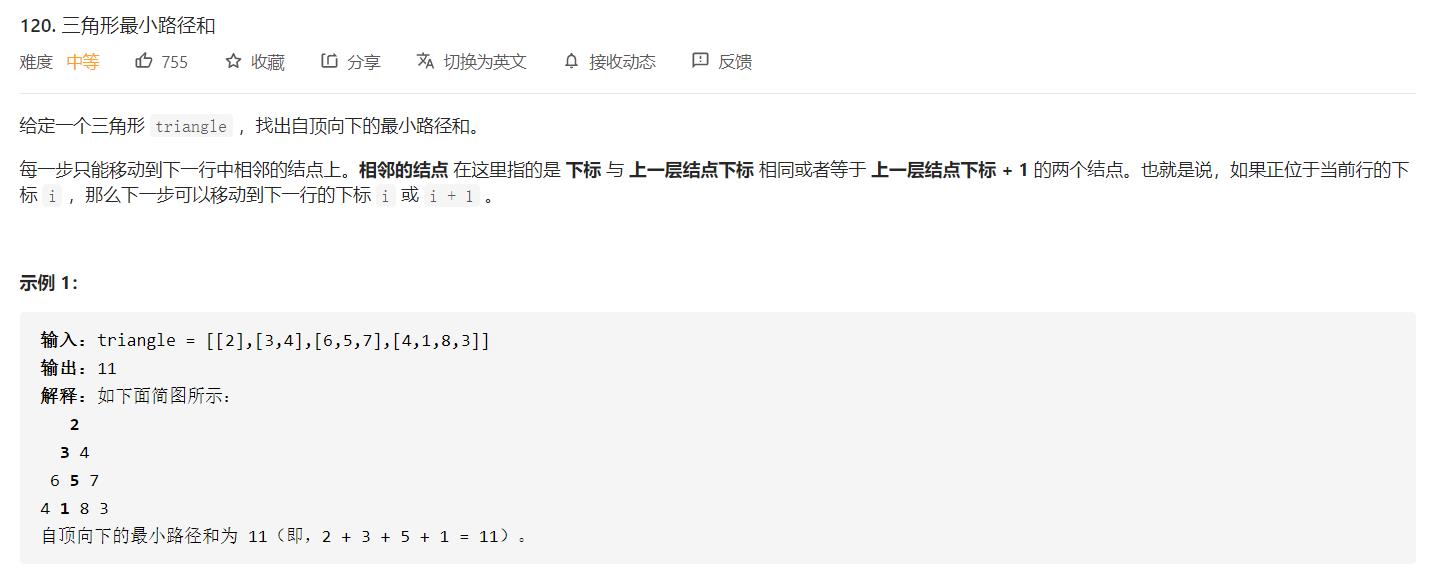
分析：

[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
相邻结点：与(i, j) 点相邻的结点为 (i + 1, j) 和 (i + 1, j + 1)。

• 若定义 f(i, j) 为 (i, j) 点到底边的最小路径和，则易知递归求解式为:
• f(i, j) = min(f(i + 1, j), f(i + 1, j + 1)) + triangle[i][j]
• 由此，我们将任一点到底边的最小路径和，转化成了与该点相邻两点到底边的最小路径和中的较小值，再加上该点本身的值。这样本题的递归解法就完成了。

class Solution {
public:
	int minimumTotal(vector<vector<int>>& triangle) {
		return dfs(triangle, 0, 0);
	}
	int dfs(vector<vector<int>>& triangle,int i,int j)
	{
		if (i == triangle.size()) return 0;
		return min(dfs(triangle, i + 1, j),dfs(triangle,i+1,j+1))+triangle[i][j];
	}
};

---

记忆化递归

• 通过一个map容器记录保存计算出来的结果.下一次如果用到了直接返回，不需要再次递归计算

class Solution {
	map<pair<int, int>, int> map;
public:
	int minimumTotal(vector<vector<int>>& triangle) {
		return dfs(triangle, 0, 0);
	}
	int dfs(vector<vector<int>>& triangle,int i,int j)
	{
		if (i == triangle.size()) return 0;
		if (map.find({ i,j }) != map.end()) return map[{i, j}];
		return map[{i, j}]=min(dfs(triangle, i + 1, j), dfs(triangle, i + 1, j + 1))+triangle[i][j];
	}
};

---

自上而下的动态规划

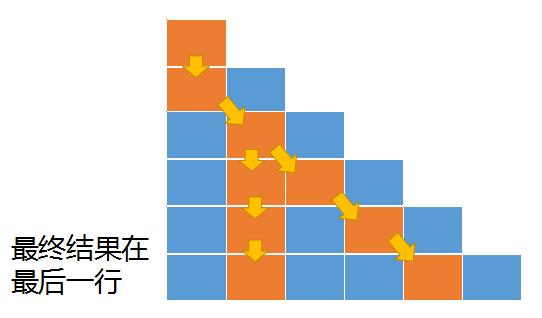
• 题目给出的例子看上去不是那么直观，现在我们把例子中的数组位置重新摆放一下。那么自顶向下的移动路线就是这样的
  
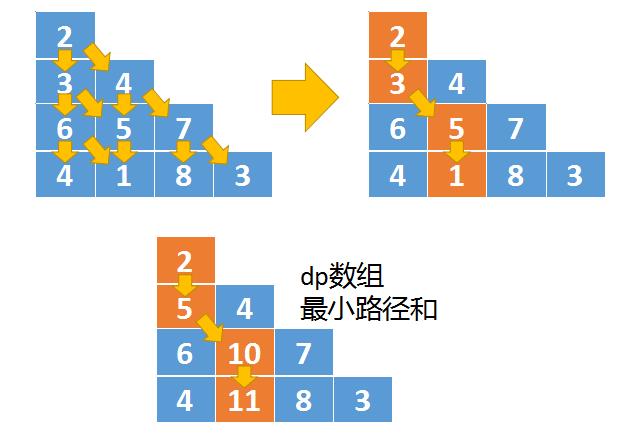
• 也就是triangle[i][j]可以向triangle[i+1][j]移动，也可以向triangle[i+1][j+1]移动
• 这个三角形的最小路径和就是2->3->5->1，
• 我们用一个dp数组保存每次移动的最小值，2->3->5->1这个路径移动后在dp数组中保存的结果就是2->5->10->11
• 反过来说，对于三角形中任意一个位置triangle[i][j]，只有两个值能移动到这个位置
• 分别是triangle[i-1][j-1]，以及triangle[i-1][j]，如下图所示
  
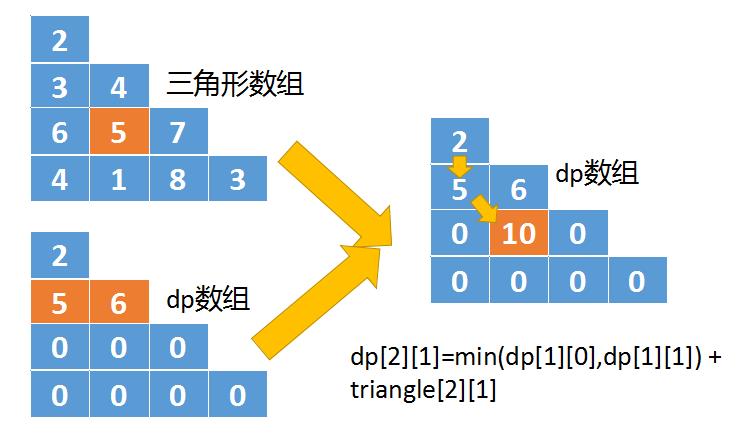
• 对于triangle[2][1]这个位置，它是从triangle[1][0]，以及triangle[1][1]这两个位置移动而来的。而这两个值我们已经先保存到dp[1][0]和dp[1][1]中了。
• 我们从dp[1][1]和dp[1][0]中选择一个较小的值，这里就是5，然后再加上triangle[2][1]的值5，将结果10保存到dp[2][1]中。
• dp转移公式为：
• dp[i][j] = min(dp[i-1][j-1],dp[i-1][j])+triangle[i][j]
• 使用上面那个转移公式，这题基本上就可以搞定了
• 但需要注意的是，自上而下推导时，有两个特例
  
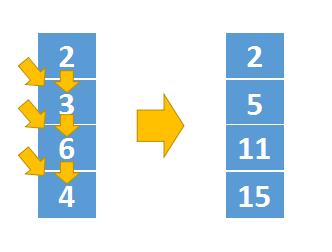
• 第一列计算的时候，如果用dp[i-1][j-1]获取斜上方值时会出现下标越界。从上图中我们也可以发现，实际上第一列计算的时候，它只有一条转移路径，我们需要单独处理，其计算公式如下，
• dp[i][0] = dp[i-1][0] + triangle[i][0]
• 第二个特例是三角形的斜边
  
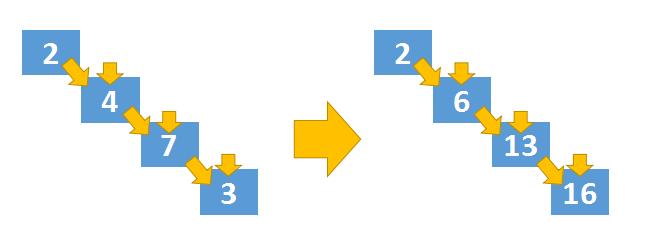
• 通过上图我们可以发现，这条斜边也是只有一条转移路径，同样也需要单独处理，其计算公式如下:
• dp[i][j] = dp[i-1][j-1] + triangle[i][j]
• 自上而下推到到最后一行就结束了，但最后一行的哪一列是最终值我们并不知道，因为很多条转移路径都会到达最后一行。所以动态规划整个计算过程结束后，我们还需要再计算一下最后一行的min值，这个min值就是最终的结果。
  
• 时间复杂度:O(N^2)
• 空间复杂度:O(N^2)

class Solution {
public:
	int minimumTotal(vector<vector<int>>& triangle) 
	{
		if (triangle.empty()) return 0;
		int r = triangle.size();//行
		vector<vector<int>> dp(triangle.size(), vector<int>(triangle[r-1].size()));
		//初始值
		dp[0][0] = triangle[0][0];
		//第一列
		for (int i = 1; i < r; i++)
			dp[i][0] = dp[i - 1][0] + triangle[i][0];
		for (int i = 1; i < r; ++i)
		{
			int j = 1;
			//注意计算的是三角形每一行的长度都不同
            //最后一列需要单独计算(斜边)，所以是从遍历的个数是size()-1
			while (j <triangle[i].size()-1)
			{
				//状态转移公式
				dp[i][j] = min(dp[i - 1][j - 1], dp[i-1][j])+triangle[i][j];
				++j;
			}
			//三角形斜边需要单独计算
			dp[i][j] = dp[i - 1][j - 1] + triangle[i][j];
		}
		//最后一行保存了每条路径的计算结果，对最后一行数组求min即为最终结果
		     int Min = INT_MAX;
			for (int j = 0; j <triangle[r-1].size(); j++)
			{
				Min = min(Min, dp[r-1][j]);
			}
			return Min;
	}
};

---

自下而上的动态规划

• 下图演示的是自下而上的推导过程
  
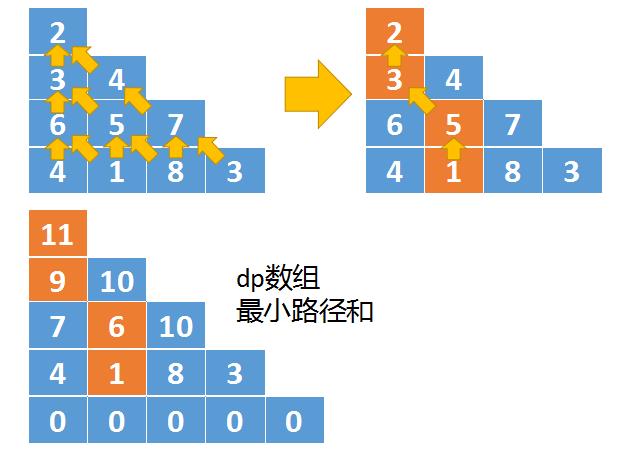
• 自下而上推导时，结果保存在第一行第一列中，因为三角形第一行只有一个元素，所以最终结果就保存在dp[0][0]中
• 此外dp数组跟自上而下比也有些变化，这里的dp数组是原始数组的行数+1
• 之所以以要多加一行，是因为状态转移公式变化导致的，为了处理一些边界条件所以增加了一行
• 以自下而上的角度看，三角形中任意一个位置triangle[i][j]，只有两个值能移动到这个这里分别是triangle[i+1][j+1]，以及triangle[i+1][j]，如下图所示
  
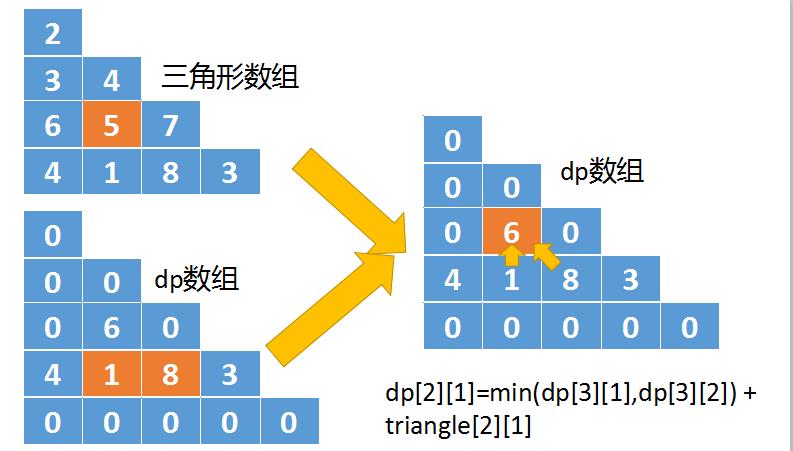
• 对于triangle[2][1]这个位置，它是从triangle[3][2]，以及triangle[3][1]这两个位置移动而来的。而这两个值保存在dp[3][2]和dp[3][1]中。
• 我们从dp[3][2]和dp[3][1]中选择一个较小的值，这里是1，然后再加上triangle[2][1]的值5，将结果6保存到dp[2][1]中。
• 其dp转移公式为：

dp[i][j] = min(dp[i+1][j+1],dp[i+1][j]) + triangle[i][j]

• 自下而上推导没有自上而下那么直观，但是省去了一些细节处理过程
• 同时最终的结果就保存在了dp[0][0]中，又省去了一次遍历求min的过程
• 时间复杂度:O(N^2)
• 空间复杂度:O(N^2)

class Solution {
public:
	int minimumTotal(vector<vector<int>>& triangle) 
	{
		if (triangle.empty()) return 0;
		int r = triangle.size();
		int c = triangle[r-1].size();//最后一行的长度
		vector<vector<int>> dp(r + 1, vector<int>(c + 1,0));
		//自下而上推导
		for (int i = r - 1; i >= 0; i--)
		{
			int j = triangle[i].size()-1;
			while (j >= 0)
			{
				//对于三角形的每一行，从右向左计算
				dp[i][j] = min(dp[i + 1][j + 1], dp[i + 1][j]) + triangle[i][j];
				--j;
			}
		}
		//最终结果就保存在第一行第一列中
		return dp[0][0];
	}
};

---

动态规划空间优化

• 我们用二维数组计算dp[i][j]时只用到了dp[i+1][j+1]和dp[i+1][j]
• 也就是说这是一个滚动更新的过程，我们只用到了上下两行数据
• 求dp[i][j]时只需要dp[i+1]这一行的数据即可，dp[i+2]，dp[i+3]…这些都不需要了。
• 于是我们可以创建一个一维数组，其长度为三角形列数+1
  
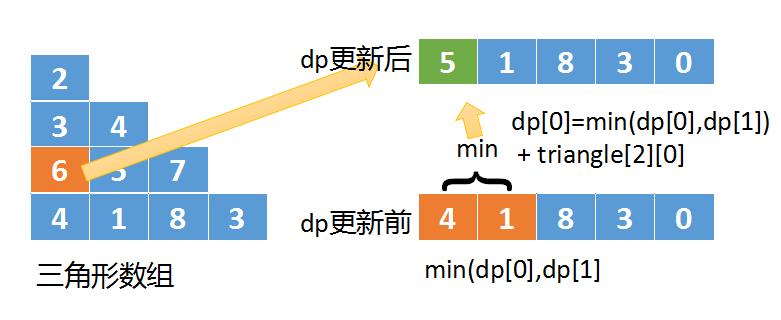
• 如上图所示，我们还是按照自下而上的方式，但这次的dp数组改成一维的了
• 计算triangle[2][0]的最小路径为:
• triangle[2][0] + min(dp[0],dp[1])
• 之后将结果5保存到dp[0]中
• 所以一维数组的状态转移方程为:
• dp[j] = min(dp[j],dp[j+1]) +triangle[i][j]
• 我们用的是自下而上的计算方式，先计算n-1行，再计算n-2行，一直到第1行
• 每行计算的时候用的是从左到右的方式，如果是从右到左计算会出现值覆盖
• 图解演示:
  
  
  
  
  
  
  
  
  
  
  

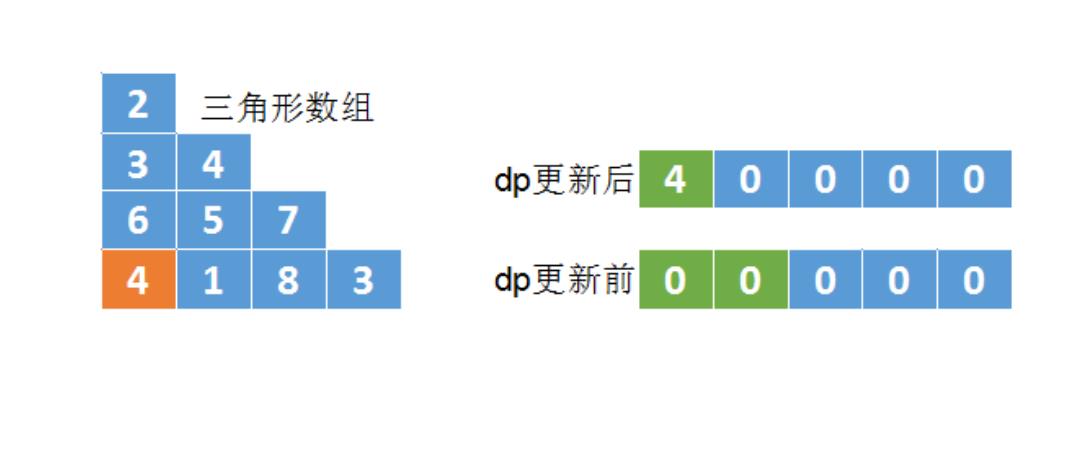
完整代码:

class Solution {
public:
	int minimumTotal(vector<vector<int>>& triangle) 
	{
		if (triangle.empty()) return 0;
		int r = triangle.size();
		int c = triangle[r-1].size();//最后一行的长度
		vector<int> dp(c + 1,0);
	    //自下而上推导
		for (int i = r - 1; i >= 0; i--)
		{
			//从左到右的方式计算
			for (int j = 0; j < triangle[i].size(); ++j)
			{
				dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j];
			}
		}
		//dp数组的第一个元素即为最终结果
		return dp[0];
	}
};