图与深度优先广度优先搜索

Posted 2021-05-14 别诺尼

图的表示

整体思路：问题——图——矩阵

邻接矩阵

两点之间是否有关系，用如下函数表示：

$$a_{ij}=1（如果i到j是联通的)$$

表示成矩阵的形式：

i\j	1	2	...
1	.	1
2	1	.
...

如果不存在方向，矩阵是对称的。

邻接表

将每一个节点表示在图上，相邻节点之间有关系，就用实线连接，可以利用箭头表示方向。

深度优先搜索（DFS）

深度优先搜索算法

从一个顶点出发，访问其所能到达的一个节点，如果存在多个节点可以到达，利用规则（如：字母表顺利、随机）选择一个。一旦到底，就返回到上一个可供选择的节点，在该节点选择其它路径。

可能使用的结构：布尔变量标记是否存在多条路径、利用堆栈回溯

前序与后序

前序：顶点最先被访问（previsit）的时刻

后序：顶点最后离开（postvisit）的时刻

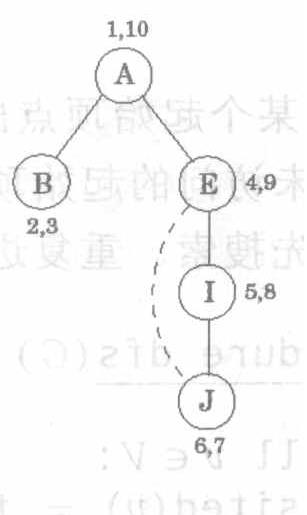
每个节点上标注的数字分别是前序与后序。

边的类型

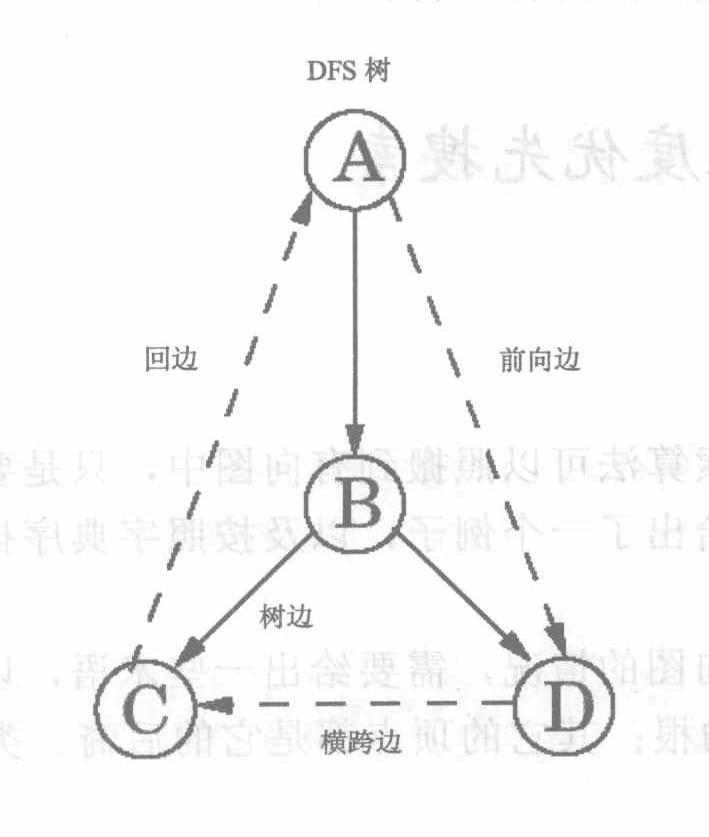
树边：实际走过的部分

前向边：树中从一个顶点指向该顶点的一个非子顶点后裔的边

回边：树中从一个顶点指向其祖先的边

横跨边：从一个顶点指向一个已经完全访问顶点的边

有向无环图

环指的是形如$v_0\to v_1\to v2 \to v_0$的循环路径

性质：有向图含有一个环当且仅当深度优先搜索过程中探测到一条回边，每个有向无环图至少含有一个源点和一个汇点。

有向有环图

连通性：如果从顶点$u$到$v$，以及$v$到$u$各存在一条路径，则称$u$与$v$是联通的。（可以理解为子群是阿贝尔群，便是联通的）

强连通部件：将这些两两之间具有连通性的节点，认为是一个大节点，然后形成的简化后的图称为强连通部件。

性质：每个有向图关于其强连通部件都是一个有向无环图。

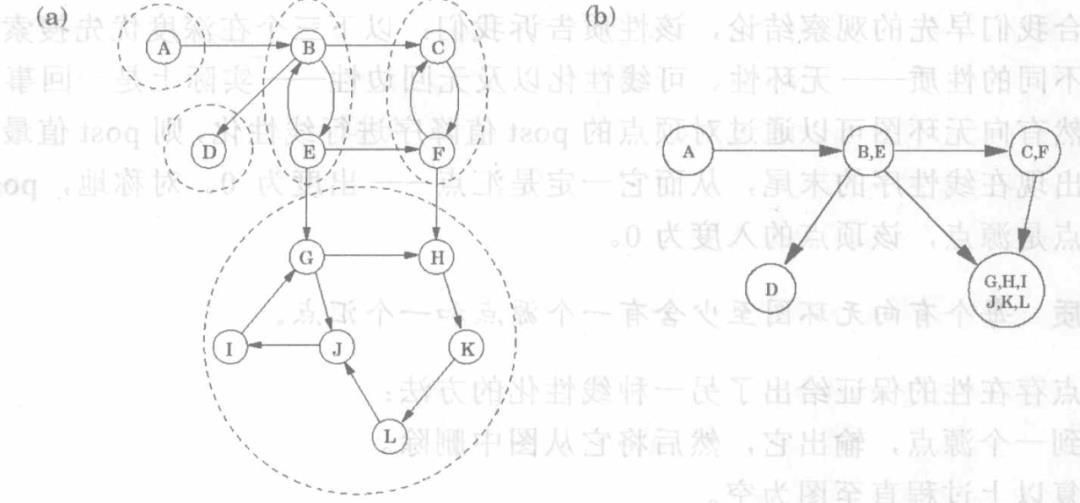
广度优先搜索（BFS）

广度优先搜索算法

讨论图论中最短距离的算法

计算从$s$到其它顶点距离的方式是，按照层次进行逐层处理，起初队列$Q$中只含有$s$（即距离为$0$的点）。对于后续距离为$d=1,2,3....$$Q$中分别曾一度只包含距离为$d$的顶点。随着这些顶点被逐个处理（从队列中删除），这些顶点的未发现邻居被插入队列。

边的长度

不同的相邻顶点之间的开销不一致，从$v\to u$的开销记为$l(v,u)$。

Dijkstra算法

在相邻两点之间具有非负距离时，计算任意两点之间的最短距离。

思想：

1.从$s$出发，$s$记为$0$，其余顶点距离为$\infin$2.记录$s$到达的临近点距离，更新距离3.除去已经走过的点，从其余点中选择一个最近点4.认为新选择的点是新的$s$点，重复步骤2，直到所有点都更新完

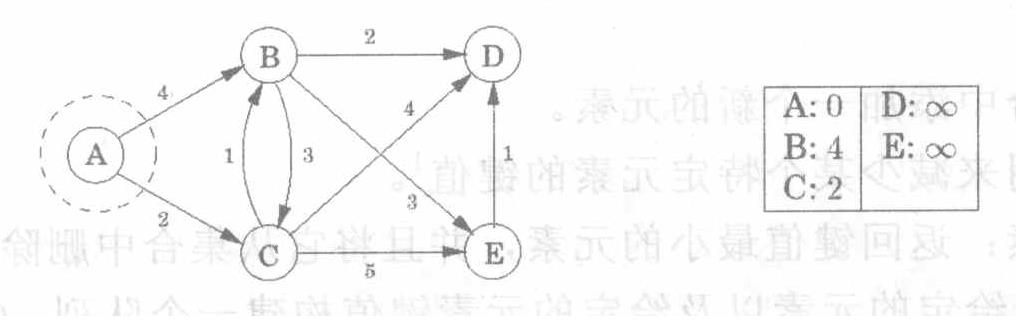
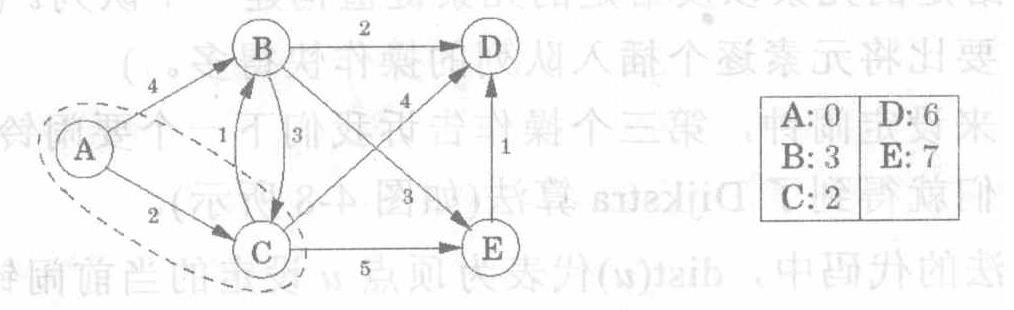
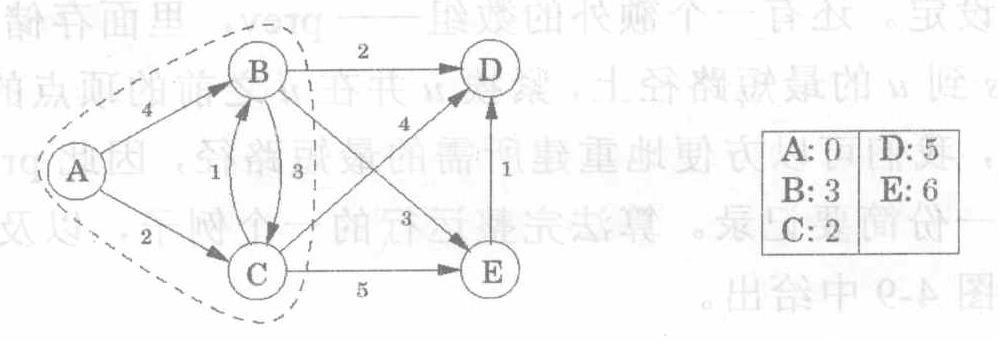
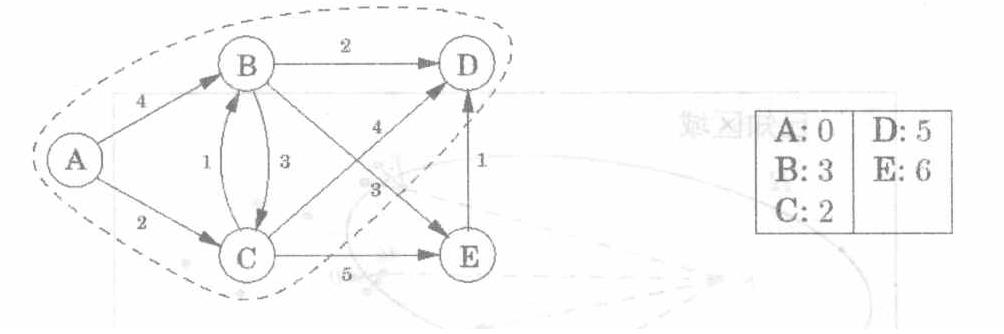
Bellman-Ford算法

Dijkstra算法只能计算不含负边的图，为计算含有负边的图引入Bellman-Ford算法。

思想：

与Dijkstra算法类似，也是通过不断更新距离达到计算最短距离的目的。但是，这里更新不是只更新最近点周围的节点的值，而是更新所有已经走过的节点的周围的节点值。

References

[1] Sanjoy Dasgupta, Christos Papadimitriou著. 王沛, 唐扬斌, 刘齐军 译. 算法概论. 清华大学出版社. 2008.