朴素贝叶斯算法基础原理

Posted 2021-04-24 AI入门学习

一、从一个案例开始

朴素贝叶斯(Native Bayes)算法是基于贝叶斯定理和特征条件独立假设的分类算法。

贝叶斯定理其实就是一个非常简单的公式，如下所示，这里先不讲公式，而是重点关注他的使用价值，因为只有理解了定理的应用意义，你才会有兴趣学下去。

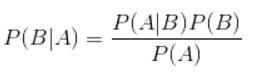
在分类算法里面应用，可以转换成下面的表达式，一眼就看明白了

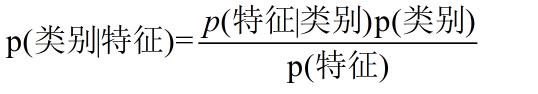
当然，这样有人可能还是不明白，我们再具体一点，加入你有一封邮件，包含：代开,增值税,发票,sep，这几个词，要预测其为垃圾邮件的概率，问题转化成P（垃圾|代开,增值税,发票,sep）只要计算出该表达式的值即可，应用全概率公式，进一步转换成下面的等式。

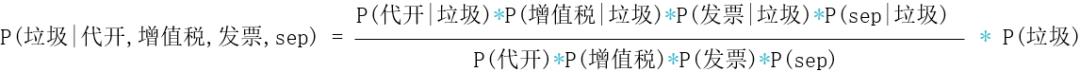
就这样，我们把公式和实际的应用联系起来了。

当然要计算上面的概率，需要我们有历史数据，于是我从我的邮箱里面复制了一些垃圾邮件，以及一些正常的邮件，并对数据做了一下简单的处理，打上了垃圾邮件和正常邮件的标签，我们就可以得到历史数据，进行计算了。

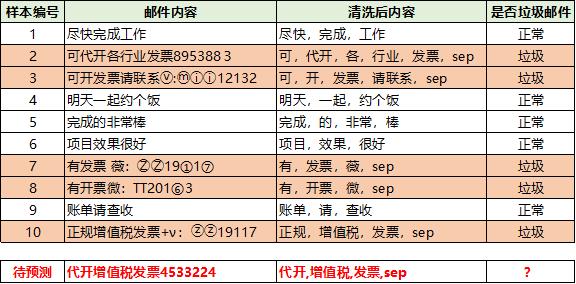
分子的概率计算,即垃圾邮件的条件下，各个词的概率：

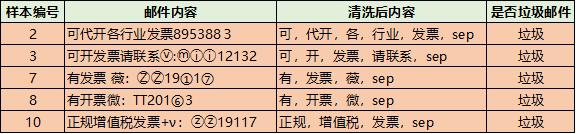
P（代开|垃圾）   = 1/5  = 0.2

P（增值税|垃圾）= 1/5  = 0.2

P（发票|垃圾）    =  4/5 = 0.8

P（sep|垃圾）     =  5/5 = 1.0

分母概率计算，即全集中每个词的概率：

P（代开）   = 1/10  = 0.1

P（增值税）= 1/10  = 0.1

P（发票）   =  4/10 = 0.4

P（sep）    =  5/10 = 0.5

计算垃圾邮件的概率，一共10个样本，5个垃圾邮件，5个正常邮件：

P(垃圾)= 5/10 = 0.5

汇总计算最后的垃圾概率：

P（垃圾|代开,增值税,发票,sep） = (0.2*0.2*0.8*1)*0.5/(0.1*0.1*0.4*0.5) = 0.8

 

我们计算下正常邮件的概率为多大，按公式直接计算，结果为0，但是直接计算，会导致很多样本都为0，所以后面会引入拉普拉斯平滑。

P（正常|代开,增值税,发票,sep） = 0

采用拉普拉斯变换计算得到,具体定义见后文，专门解决0概率问题：

P（代开|正常）   = 1/（5+1）  = 0.167

P（增值税|正常）= 1/（5+1）  =  0.167

P（发票|正常）    = 1/（5+1） =  0.167

P（sep|正常）     = 1/（5+1） =  0.167

P（正常|代开,增值税,发票,sep） = (0.167*0.167*0.167*0.167)*0.5/(0.1*0.1*0.4*0.5) =0.194

通过上面的案例，我们应该对贝叶斯定理有了一定的了解，并且知道贝叶斯能解决什么问题了，但是要成为高手，这只是开胃菜，还有很多需要学的，下面我们一一讲解。

当然我，我们用Python内置的库，就更简单了，几行代码就搞定了。

data = ['尽快，完成，工作','可，代开，各，行业，发票，sep','可，开，发票，请联系，sep','明天，一起，约个饭','完成，的，非常，棒','项目，效果，很好','有，发票，薇，sep','有，开票，微，sep','账单，请，查收','正规，增值税，发票，sep']label=[0,1,1,0,0,0,1,1,0,1]

vectorizer_word = TfidfVectorizer()vectorizer_word.fit(data,)#vectorizer_word.vocabulary_

train = vectorizer_word.transform(data)test = vectorizer_word.transform(['代开,增值税,发票,sep'])

from sklearn.naive_bayes import MultinomialNBclf = MultinomialNB()clf.fit(train.toarray(), label)clf.predict(test.toarray(),)array([1])clf.predict_proba(test.toarray(),)array([[0.19710234, 0.80289766]])算出来的概率也是0.80左

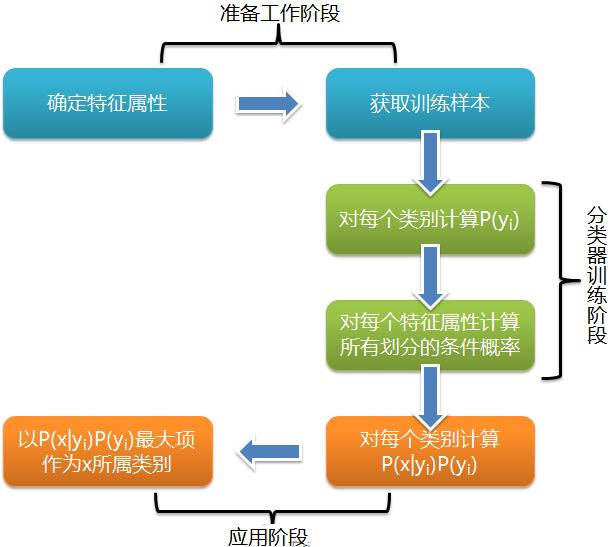
通过上述案例可以看到，贝叶斯算法的一个基本流程如下

二、贝叶斯定理概述

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。贝叶斯定理太有用了，不管是在投资领域，还是机器学习，或是日常生活中高手几乎都在用到它。

生命科学家用贝叶斯定理研究基因是如何被控制的，教育学家意识到,学生的学习过程其实就是贝叶斯法则的运用，基金经理用贝叶斯法则找到投资策略，谷歌用贝叶斯定理改进搜索功能，帮助用户过滤垃圾邮件，无人驾驶汽车接收车顶传感器收集到的路况和交通数据运用贝叶斯定理更新从地图上获得的信息，人工智能、机器翻译中大量用到贝叶斯定理，比如肝癌的检测、垃圾邮件的过滤。

贝叶斯定理由英国数学家贝叶斯 ( Thomas Bayes 1702-1761 ) 发展，用来描述两个条件概率之间的关系，比如 P(A|B) 和 P(B|A)。主要用于文本分类。

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法

朴素贝叶斯分类（NBC）是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法，先通过已给定的训练集，以特征词之间独立作为前提假设，学习从输入到输出的联合概率分布，再基于学习到的模型，输入X求出使得后验概率最大的输出Y 。 

设有样本数据集D={d1,d2,...,dn}，对应样本数据的特征属性集为X={x1,x2,...,xd}类变量为Y={y1,y2,...ym} ，即D可以分为ym类别。其中{x1,x2,...,xd} 相互独立且随机，则Y的先验概率P(Y) ，Y的后验概率P(Y|X) ，由朴素贝叶斯算法可得，后验概率可以由先验概率P(Y) ,证据P(X) ,类条件概率P(X|Y)计算出

朴素贝叶斯基于各特征之间相互独立，在给定类别为y的情况下，上式可以进一步表示为下式：

由以上两式可以计算出后验概率为：

由于P(X)的大小是固定不变的，因此在比较后验概率时，只比较上式的分子部分即可,因此可以得到一个样本数据属于类别yi的朴素贝叶斯计算：

对于上述例题，就得到如下的表达式

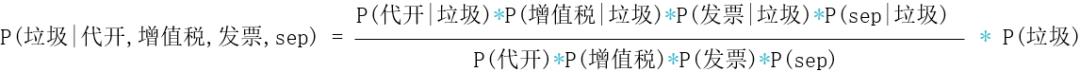
三、零概率问题

零概率问题，即测试样例的标签属性中，出现了模型训练过程中没有记录的值，或者某个分类没有记录的值，从而出现该标签属性值的出现概率 P(wi|Ci) = 0 的现象。因为 P(w|Ci) 等于各标签属性值 P(wi|Ci) 的乘积，当分类 Ci 中某一个标签属性值的概率为 0，最后的 P(w|Ci) 结果也为 0。很显然，这不能真实地代表该分类出现的概率

解决方法：拉普拉斯修正，又叫拉普拉斯平滑，这是为了解决零概率问题而引入的处理方法。其修正过程：

浮点数溢出问题：在计算 P(w|Ci) 时，各标签属性概率的值可能很小，而很小的数再相乘，可能会导致浮点数溢出。解决方法：对 P(w|Ci) 取对数，把概率相乘转换为相加。

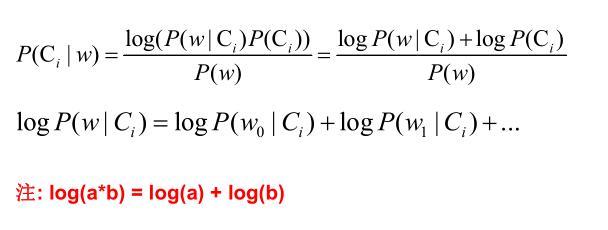
四、连续型变量概率计算

对于离散型变量，直接统计频数分布就可以了。对于连续型的变量，为了计算对应的概率，此时又引入了一个假设，假设特征的分布为正态分布，计算样本的均值和方差，然后通过密度函数计算取值时对应的概率

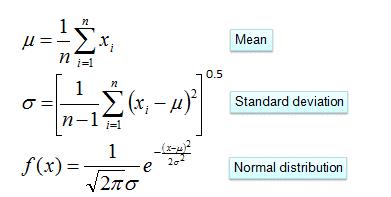
示例如下

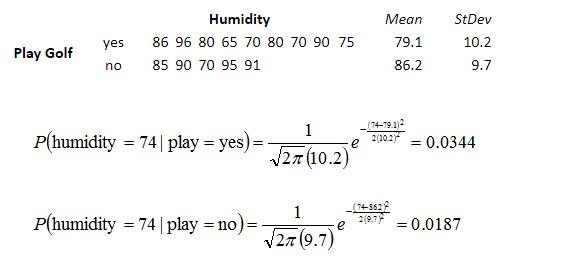
从上面的例子可以看出，朴素贝叶斯假设样本特征相互独立，而且连续型的特征分布符合正态分布，这样的假设前提是比较理想化的，所以称之为"朴素"贝叶斯，因为实际数据并不一定会满足这样的要求。

五、Python库中的贝叶斯

在scikit-learn库，根据特征数据的先验分布不同，给我们提供了5种不同的朴素贝叶斯分类算法（sklearn.naive_bayes: Naive Bayes模块），分别是伯努利朴素贝叶斯（BernoulliNB），类朴素贝叶斯（CategoricalNB），高斯朴素贝叶斯（GaussianNB）、多项式朴素贝叶斯（MultinomialNB）、补充朴素贝叶斯（ComplementNB） 。

naive_bayes.BernoulliNB	Naive Bayes classifier for multivariate Bernoulli models.
naive_bayes.CategoricalNB	Naive Bayes classifier for categorical features
naive_bayes.ComplementNB	The Complement Naive Bayes classifier described in Rennie et al.
naive_bayes.GaussianNB	Gaussian Naive Bayes (GaussianNB)
naive_bayes.MultinomialNB	Naive Bayes classifier for multinomial models

这5种算法适合应用在不同的数据场景下，我们应该根据特征变量的不同选择不同的算法，下面是一些常规的区别和介绍。

GaussianNB

高斯朴素贝叶斯，特征变量是连续变量，符合高斯分布，比如说人的身高，物体的长度。

这种模型假设特征符合高斯分布。

MultinomialNB

特征变量是离散变量，符合多项分布，在文档分类中特征变量体现在一个单词出现的次数，或者是单词的 TF-IDF 值等。不支持负数，所以输入变量特征的时候，别用StandardScaler进行标准化数据，可以使用MinMaxScaler进行归一化。

这个模型假设特征复合多项式分布，是一种非常典型的文本分类模型，模型内部带有平滑参数。

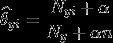
ComplementNB

是MultinomialNB模型的一个变种，实现了补码朴素贝叶斯(CNB)算法。CNB是标准多项式朴素贝叶斯(MNB)算法的一种改进，比较适用于不平衡的数据集，在文本分类上的结果通常比MultinomialNB模型好，具体来说，CNB使用来自每个类的补数的统计数据来计算模型的权重。CNB的发明者的研究表明，CNB的参数估计比MNB的参数估计更稳定。

BernoulliNB

模型适用于多元伯努利分布，即每个特征都是二值变量，如果不是二值变量，该模型可以先对变量进行二值化，在文档分类中特征是单词是否出现，如果该单词在某文件中出现了即为1，否则为0。在文本分类的示例中，统计词语是否出现的向量(word occurrence vectors)(而非统计词语出现次数的向量(word count vectors))可以用于训练和使用这个分类器。BernoulliNB 可能在一些数据集上表现得更好，特别是那些更短的文档。如果时间允许，建议对两个模型都进行评估。

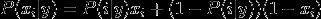
CategoricalNB

对分类分布的数据实施分类朴素贝叶斯算法，专用于离散数据集， 它假定由索引描述的每个特征都有其自己的分类分布。对于训练集中的每个特征 X，CategoricalNB估计以类y为条件的X的每个特征i的分类分布。样本的索引集定义为J=1,…,m，m作为样本数。

 

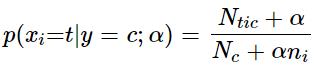
案例测试

from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB,ComplementNB from sklearn.datasets import load_breast_cancerfrom sklearn.model_selection import cross_val_scoreX,y = load_breast_cancer().data,load_breast_cancer().targetnb1= GaussianNB()nb2= MultinomialNB()nb3= BernoulliNB()nb4= ComplementNB()for model in [nb1,nb2,nb3,nb4]: scores=cross_val_score(model,X,y,cv=10,scoring='accuracy') print("Accuracy:{:.4f}".format(scores.mean())) Accuracy:0.9368Accuracy:0.8928Accuracy:0.6274Accuracy:0.8928  from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB,ComplementNB ,CategoricalNBfrom sklearn.datasets import load_irisfrom sklearn.model_selection import cross_val_scoreX,y = load_iris().data,load_iris().targetgn1 = GaussianNB()gn2 = MultinomialNB()gn3 = BernoulliNB() gn4 = ComplementNB()gn5 = CategoricalNB(alpha=1)for model in [gn1,gn2,gn3,gn4,gn5]: scores = cross_val_score(model,X,y,cv=10,scoring='accuracy') print("Accuracy:{:.4f}".format(scores.mean()))Accuracy:0.9533Accuracy:0.9533Accuracy:0.3333Accuracy:0.6667Accuracy:0.9267 进行one-hot变化，可以发现BernoulliNB分类准确率还是很高的from sklearn import preprocessing enc = preprocessing.OneHotEncoder() # 创建对象

from sklearn.datasets import load_irisX,y = load_iris().data,load_iris().target

enc.fit(X) array = enc.transform(X).toarray() 

from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB,ComplementNB ,CategoricalNBfrom sklearn.datasets import load_irisfrom sklearn.model_selection import cross_val_scoreX,y = load_iris().data,load_iris().targetgn1 = GaussianNB()gn2 = MultinomialNB()gn3 = BernoulliNB()gn4 = ComplementNB()for model in [gn1,gn2,gn3,gn4]: scores=cross_val_score(model,array,y,cv=10,scoring='accuracy') print("Accuracy:{:.4f}".format(scores.mean()))Accuracy:0.8933Accuracy:0.9333Accuracy:0.9333Accuracy:0.9400

 

推荐阅读：

↓扫描关注本号↓