QM for Windows 之网络流模型（最短路径问题）

Posted 2021-04-23 梦常徒花

网络流问题是一类特殊的线性规划问题，如前面提到过的运输问题，除了可以写成线性规划的形式，还能将该问题构建成网络的形式求解。今天介绍网络流基本问题之一的 最短路径问题 的QM for Windows求解方法。

---

最短路径问题是确定初始点与几个目标点之间的最短距离。在生产实践，运输管理中，诸如工艺路线安排，管道线网铺设、设备更新等问题都可建模为最短路问题。经典的求解算法有基于最优性原理的标号法的 算法。而本文主要介绍如何用MQ for Windows已有的模块求解此类问题。

例： 在1号小区有一个快递网点，快递小哥需要给位于8号小区的顾客派件，途中可能会经过若干个小区。为提高配送效率，快递小哥需要选择一条 最快的路径 到达8号小区。（我们将上述问题抽象成下图所示的网络图，弧上的权值表示小区间的距离，这种弧上有权值的图称为赋权图。该问题可以基于图论的方法在网络上求解）。

Step1 ：启动QM for Windows程序，点击顶端“VIEW”->"Module Tree"，打开右侧的模型列表，点击“Networks”，点击下拉列表的“Shortest Route”，初始化模型。“Branches”是设置边的数量（支流）、根据要求设置网络类型（无向图、有向图）、右侧命名可忽略。

Step2 ：输入每一条边的信息（起点、终点、边的权值），右上角输入所要求解问题的起点和终点（1、8）。输数据的时候可以按照起点从小到大，终点不小于起点的顺序遍历着填，以保证在图较密集时能不遗漏。

Step3 ：点击“Solve”即解得的最短路方案。（不同的起始点组合，可以点击左上方“Edit Data”返回后修改“Origin”和“Destination”）

求解结果为：1 -> 2 -> 4 -> 8，总的最短路程为：13

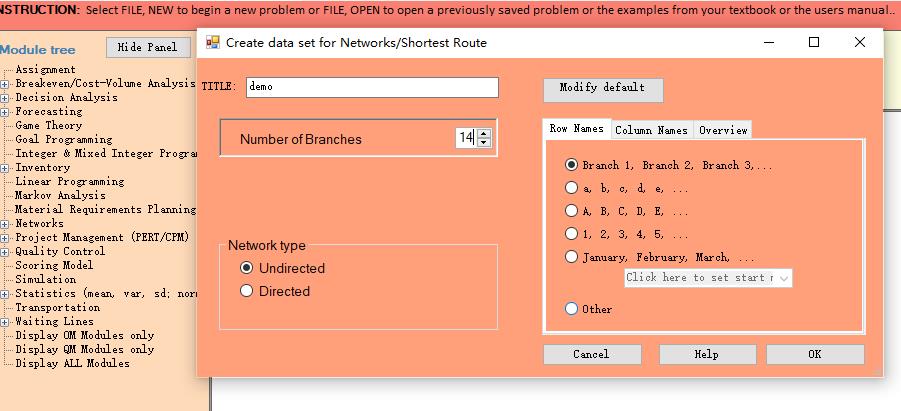
推荐文章：

---

图源：徒花君 | 部分来源网络

编辑：徒花君

参考文献：

1.伯纳德·W. 泰勒 数据、模型与决策 (12th)[M]. 北京：中国人民大学出版社.2019. 

2.傅家良.运筹学方法与模型 第2版[M].上海：复旦大学出版社.2014.