HMM(隐马尔可夫)中文分词
Posted 自然语言处理及深度学习
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了HMM(隐马尔可夫)中文分词相关的知识,希望对你有一定的参考价值。
一、隐马尔可夫模型
隐马尔可夫模型(Hidden Markov Model,HMM)是用来描述一个含有隐含未知参数的马尔可夫过程。
1、举例理解
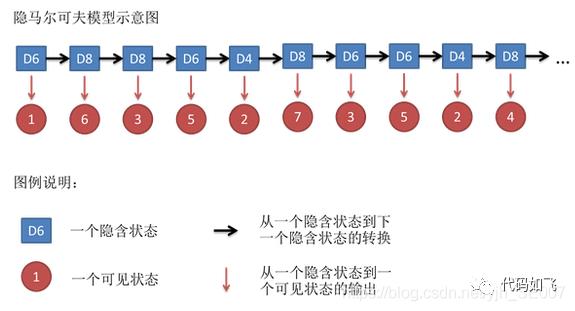
假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子(称这个骰子为D6),6个面,每个面(1,2,3,4,5,6)出现的概率是1/6。第二个骰子是个四面体(称这个骰子为D4),每个面(1,2,3,4)出现的概率是1/4。第三个骰子有八个面(称这个骰子为D8),每个面(1,2,3,4,5,6,7,8)出现的概率是1/8。
假设我们开始掷骰子,我们先从三个骰子里挑一个,挑到每一个骰子的概率都是1/3。然后我们掷骰子,得到一个数字,1,2,3,4,5,6,7,8中的一个。不停的重复上述过程,我们会得到一串数字,每个数字都是1,2,3,4,5,6,7,8中的一个。例如我们可能得到这么一串数字(掷骰子10次):1 6 3 5 2 7 3 5 2 4
这串数字叫做可见状态链。但是在隐马尔可夫模型中,我们不仅仅有这么一串可见状态链,还有一串隐含状态链。在这个例子里,这串隐含状态链就是你用的骰子的序列。比如,隐含状态链有可能是:D6 D8 D8 D6 D4 D8 D6 D6 D4 D8
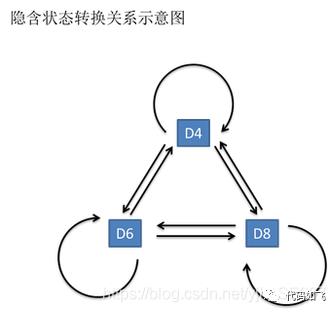
一般来说,HMM中说到的马尔可夫链其实是指隐含状态链,因为隐含状态(骰子)之间存在转换概率(transition probability)。在我们这个例子里,D6的下一个状态是D4,D6,D8的概率都是1/3。D4,D8的下一个状态是D4,D6,D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚,但是我们其实是可以随意设定转换概率的。比如,我们可以这样定义,D6后面不能接D4,D6后面是D6的概率是0.9,是D8的概率是0.1。这样就是一个新的HMM。
同样的,尽管可见状态之间没有转换概率,但是隐含状态和可见状态之间有一个概率叫做输出概率(emission probability)。就我们的例子来说,六面骰(D6)产生1的输出概率是1/6。产生2,3,4,5,6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如,我有一个被赌场动过手脚的六面骰子,掷出来是1的概率更大,是1/2,掷出来是2,3,4,5,6的概率是1/10。
2、例子抽象
3种不同情况的骰子,即为:状态值集合(StatusSet)
所有可能出现的结果值(1、2、3、4、5、6、7、8):观察值集合(ObservedSet)。
选择不同骰子之间的概率:转移概率矩阵(TransProbMatrix ),状态间转移的概率。
在拿到某个骰子,投出某个观测值的概率:发射概率矩阵(EmitProbMatrix )-即:拿到D6这个骰子,投出6的概率是1/6。最初一次的状态:初始状态概率分布(InitStatus )。
所以,很容易得到,计算概率的方法就是,初始状态概率分布(InitStatus )、发射概率矩阵(EmitProbMatrix )、转移概率矩阵(TransProbMatrix )的乘积。
当某个状态序列的概率值最大,则该状态序列即为,出现该观测值的情况下,最可能出现的状态序列。
二、维特比算法
维特比算法(Viterbi algorithm)是一种动态规划算法。它用于寻找最有可能产生观测事件序列的维特比路径——隐含状态序列,特别是在马尔可夫信息源上下文和隐马尔可夫模型中。
1、算法原理
维特比算法就是求所有观测序列中的最优,如下图所示,我们要求从S到E的最优序列,中间有3个时刻,每个时刻都有对应的不同观察的概率,下图中每个时刻不同的观测标签有3个。
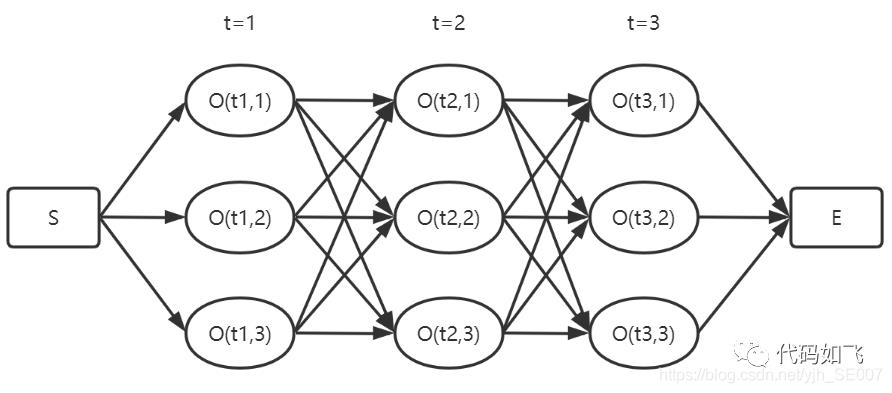
求所有路径中最优路径,最容易想到的就是暴力解法,直接把所有路径全部计算出来,然后找出最优的。这方法理论上是可行,但当序列很长时,时间复杂夫很高。而且进行了大量的重复计算,viterbi算法就是用动态规划的方法就减少这些重复计算。
viterbi算法是每次记录到当前时刻,每个观察标签的最优序列,如下图,假设在t时刻已经保存了从0到t时刻的最优路径,那么t+1时刻只需要计算从t到t+1的最优就可以了,图中红箭头表示从t时刻到t+1时刻,观测标签为1,2,3的最优。
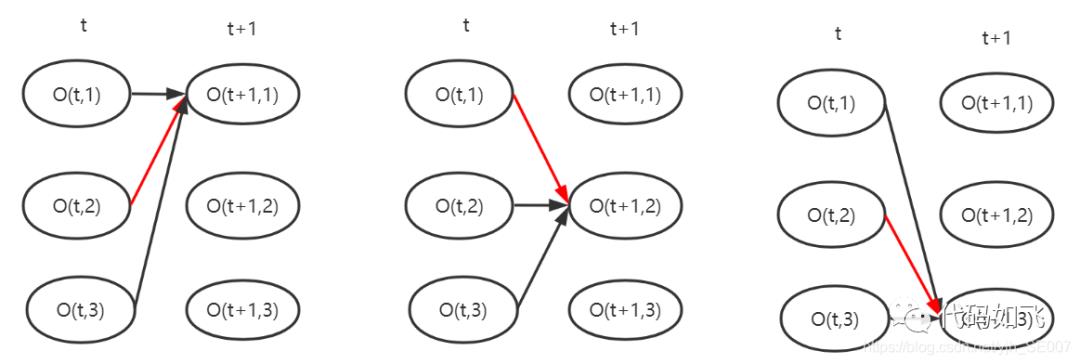
每次只需要保存到当前位置最优路径,之后循环向后走。到结束时,从最后一个时刻的最优值回溯到开始位置,回溯完成后,这个从开始到结束的路径就是最优的。
2、代码实现
import numpy as np
def viterbi_decode(nodes, trans):
"""
Viterbi算法求最优路径
其中 nodes.shape=[seq_len, num_labels],
trans.shape=[num_labels, num_labels].
"""
# 获得输入状态序列的长度,以及观察标签的个数
seq_len, num_labels = len(nodes), len(trans)
# 简单起见,先不考虑发射概率,直接用起始0时刻的分数
scores = nodes[0].reshape((-1, 1))
paths = []
# 递推求解上一时刻t-1到当前时刻t的最优
for t in range(1, seq_len):
# scores 表示起始0到t-1时刻的每个标签的最优分数
scores_repeat = np.repeat(scores, num_labels, axis=1)
# observe当前时刻t的每个标签的观测分数
observe = nodes[t].reshape((1, -1))
observe_repeat = np.repeat(observe, num_labels, axis=0)
# 从t-1时刻到t时刻最优分数的计算,这里需要考虑转移分数trans
M = scores_repeat + trans + observe_repeat
# 寻找到t时刻的最优路径
scores = np.max(M, axis=0).reshape((-1, 1))
idxs = np.argmax(M, axis=0)
# 路径保存
paths.append(idxs.tolist())
best_path = [0] * seq_len
best_path[-1] = np.argmax(scores)
# 最优路径回溯
for i in range(seq_len-2, -1, -1):
idx = best_path[i+1]
best_path[i] = paths[i][idx]
return best_path
三、HMM模型
HMM的典型模型是一个五元组:
StatusSet: 状态值集合
ObservedSet: 观察值集合
TransProbMatrix: 转移概率矩阵
EmitProbMatrix: 发射概率矩阵
InitStatus: 初始状态分布
基本假设
HMM模型的三个基本假设如下:
有限历史性假设:
P(Status[i]|Status[i-1],Status[i-2],… Status[1]) = P(Status[i]|Status[i-1])
齐次性假设(状态和当前时刻无关):
P(Status[i]|Status[i-1]) = P(Status[j]|Status[j-1])
观察值独立性假设(观察值只取决于当前状态值):
P(Observed[i]|Status[i],Status[i-1],…,Status[1]) = P(Observed[i]|Status[i])
1、状态值集合(StatusSet)
(B, M, E, S): {B:begin, M:middle, E:end, S:single}。分别代表每个状态代表的是该字在词语中的位置,B代表该字是词语中的起始字,M代表是词语中的中间字,E代表是词语中的结束字,S则代表是单字成词。
如:
给你一个隐马尔科夫链的例子。
可以标注为:
给/S 你/S 一个/BE 隐马尔科夫链/BMMMME 的/S 例子/BE 。/S
2、观察值集合(ObservedSet)
就是所有汉字(东南西北你我他…),甚至包括标点符号所组成的集合。
状态值也就是我们要求的值,在HMM模型中文分词中,我们的输入是一个句子(也就是观察值序列),输出是这个句子中每个字的状态值。
3、初始状态概率分布(InitStatus )
如:
B -0.26268660809250016
E -3.14e+100
M -3.14e+100
S -1.4652633398537678
数值是对概率值取【对数】之后的结果(可以让概率【相乘】的计算变成对数【相加】)。其中-3.14e+100作为负无穷,也就是对应的概率值是0。
也就是句子的第一个字属于{B,E,M,S}这四种状态的概率。
4、转移概率矩阵(TransProbMatrix )
【有限历史性假设】
转移概率是马尔科夫链。Status(i)只和Status(i-1)相关,这个假设能大大简化问题。所以,它其实就是一个4x4(4就是状态值集合的大小)的二维矩阵。矩阵的横坐标和纵坐标顺序是BEMS x BEMS。(数值是概率求对数后的值)
5、发射概率矩阵(EmitProbMatrix )
【观察值独立性假设】
P(Observed[i], Status[j]) = P(Status[j]) * P(Observed[i]|Status[j])
其中,P(Observed[i]|Status[j])这个值就是从EmitProbMatrix中获取。
四、代码实现
import pandas as pd
import codecs
from numpy import *
import numpy as np
import sys
import re
STATES = ['B', 'M', 'E', 'S']
array_A = {} #状态转移概率矩阵
array_B = {} #发射概率矩阵
array_E = {} #测试集存在的字符,但在训练集中不存在,发射概率矩阵
array_Pi = {} #初始状态分布
word_set = set() #训练数据集中所有字的集合
count_dic = {} #‘B,M,E,S’每个状态在训练集中出现的次数
line_num = 0 #训练集语句数量
#初始化所有概率矩阵
def Init_Array():
for state0 in STATES:
array_A[state0] = {}
for state1 in STATES:
array_A[state0][state1] = 0.0
for state in STATES:
array_Pi[state] = 0.0
array_B[state] = {}
array_E = {}
count_dic[state] = 0
#对训练集获取状态标签
def get_tag(word):
tag = []
if len(word) == 1:
tag = ['S']
elif len(word) == 2:
tag = ['B', 'E']
else:
num = len(word) - 2
tag.append('B')
tag.extend(['M'] * num)
tag.append('E')
return tag
#将参数估计的概率取对数,对概率0取无穷小-3.14e+100
def Prob_Array():
for key in array_Pi:
if array_Pi[key] == 0:
array_Pi[key] = -3.14e+100
else:
array_Pi[key] = log(array_Pi[key] / line_num)
for key0 in array_A:
for key1 in array_A[key0]:
if array_A[key0][key1] == 0.0:
array_A[key0][key1] = -3.14e+100
else:
array_A[key0][key1] = log(array_A[key0][key1] / count_dic[key0])
# print(array_A)
for key in array_B:
for word in array_B[key]:
if array_B[key][word] == 0.0:
array_B[key][word] = -3.14e+100
else:
array_B[key][word] = log(array_B[key][word] /count_dic[key])
#将字典转换成数组
def Dic_Array(array_b):
tmp = np.empty((4,len(array_b['B'])))
for i in range(4):
for j in range(len(array_b['B'])):
tmp[i][j] = array_b[STATES[i]][list(word_set)[j]]
return tmp
#判断一个字最大发射概率的状态
def dist_tag():
array_E['B']['begin'] = 0
array_E['M']['begin'] = -3.14e+100
array_E['E']['begin'] = -3.14e+100
array_E['S']['begin'] = -3.14e+100
array_E['B']['end'] = -3.14e+100
array_E['M']['end'] = -3.14e+100
array_E['E']['end'] = 0
array_E['S']['end'] = -3.14e+100
def dist_word(word0,word1,word2,array_b):
if dist_tag(word0,array_b) == 'S':
array_E['B'][word1] = 0
array_E['M'][word1] = -3.14e+100
array_E['E'][word1] = -3.14e+100
array_E['S'][word1] = -3.14e+100
return
#Viterbi算法求测试集最优状态序列
def Viterbi(sentence,array_pi,array_a,array_b):
tab = [{}] #动态规划表
path = {}
if sentence[0] not in array_b['B']:
for state in STATES:
if state == 'S':
array_b[state][sentence[0]] = 0
else:
array_b[state][sentence[0]] = -3.14e+100
for state in STATES:
tab[0][state] = array_pi[state] + array_b[state][sentence[0]]
# print(tab[0][state])
#tab[t][state]表示时刻t到达state状态的所有路径中,概率最大路径的概率值
path[state] = [state]
for i in range(1,len(sentence)):
tab.append({})
new_path = {}
# if sentence[i] not in array_b['B']:
# print(sentence[i-1],sentence[i])
for state in STATES:
if state == 'B':
array_b[state]['begin'] = 0
else:
array_b[state]['begin'] = -3.14e+100
for state in STATES:
if state == 'E':
array_b[state]['end'] = 0
else:
array_b[state]['end'] = -3.14e+100
for state0 in STATES:
items = []
# if sentence[i] not in word_set:
# array_b[state0][sentence[i]] = -3.14e+100
# if sentence[i] not in array_b[state0]:
# array_b[state0][sentence[i]] = -3.14e+100
# print(sentence[i] + state0)
# print(array_b[state0][sentence[i]])
for state1 in STATES:
# if tab[i-1][state1] == -3.14e+100:
# continue
# else:
if sentence[i] not in array_b[state0]: #所有在测试集出现但没有在训练集中出现的字符
if sentence[i-1] not in array_b[state0]:
prob = tab[i - 1][state1] + array_a[state1][state0] + array_b[state0]['end']
else:
prob = tab[i - 1][state1] + array_a[state1][state0] + array_b[state0]['begin']
# print(sentence[i])
# prob = tab[i-1][state1] + array_a[state1][state0] + array_b[state0]['other']
else:
prob = tab[i-1][state1] + array_a[state1][state0] + array_b[state0][sentence[i]] #计算每个字符对应STATES的概率
# print(prob)
items.append((prob,state1))
# print(sentence[i] + state0)
# print(array_b[state0][sentence[i]])
# print(sentence[i])
# print(items)
best = max(items) #bset:(prob,state)
# print(best)
tab[i][state0] = best[0]
# print(tab[i][state0])
new_path[state0] = path[best[1]] + [state0]
path = new_path
prob, state = max([(tab[len(sentence) - 1][state], state) for state in STATES])
return path[state]
#根据状态序列进行分词
def tag_seg(sentence,tag):
word_list = []
start = -1
started = False
if len(tag) != len(sentence):
return None
if len(tag) == 1:
word_list.append(sentence[0]) #语句只有一个字,直接输出
else:
if tag[-1] == 'B' or tag[-1] == 'M': #最后一个字状态不是'S'或'E'则修改
if tag[-2] == 'B' or tag[-2] == 'M':
tag[-1] = 'S'
else:
tag[-1] = 'E'
for i in range(len(tag)):
if tag[i] == 'S':
if started:
started = False
word_list.append(sentence[start:i])
word_list.append(sentence[i])
elif tag[i] == 'B':
if started:
word_list.append(sentence[start:i])
start = i
started = True
elif tag[i] == 'E':
started = False
word = sentence[start:i + 1]
word_list.append(word)
elif tag[i] == 'M':
continue
return word_list
if __name__ == '__main__':
trainset = open('CTBtrainingset.txt', encoding='utf-8') #读取训练集
testset = open('testset.txt', encoding='utf-8') #读取测试集
# trainlist = []
Init_Array()
for line in trainset:
line = line.strip()
# trainlist.append(line)
line_num += 1
word_list = []
for k in range(len(line)):
if line[k] == ' ':continue
word_list.append(line[k])
# print(word_list)
word_set = word_set | set(word_list) #训练集所有字的集合
line = line.split(' ')
# print(line)
line_state = [] #这句话的状态序列
for i in line:
line_state.extend(get_tag(i))
# print(line_state)
array_Pi[line_state[0]] += 1 # array_Pi用于计算初始状态分布概率
for j in range(len(line_state)-1):
# count_dic[line_state[j]] += 1 #记录每一个状态的出现次数
array_A[line_state[j]][line_state[j+1]] += 1 #array_A计算状态转移概率
for p in range(len(line_state)):
count_dic[line_state[p]] += 1 # 记录每一个状态的出现次数
for state in STATES:
if word_list[p] not in array_B[state]:
array_B[state][word_list[p]] = 0.0 #保证每个字都在STATES的字典中
# if word_list[p] not in array_B[line_state[p]]:
# # print(word_list[p])
# array_B[line_state[p]][word_list[p]] = 0
# else:
array_B[line_state[p]][word_list[p]] += 1 # array_B用于计算发射概率
Prob_Array() #对概率取对数保证精度
print('参数估计结果')
print('初始状态分布')
print(array_Pi)
print('状态转移矩阵')
print(array_A)
print('发射矩阵')
print(array_B)
output = ''
for line in testset:
line = line.strip()
tag = Viterbi(line, array_Pi, array_A, array_B)
# print(tag)
seg = tag_seg(line, tag)
# print(seg)
list = ''
for i in range(len(seg)):
list = list + seg[i] + '/'
# print(list)
output = output + list + '\n'
print(output)
outputfile = open('output.txt', mode='w', encoding='utf-8')
outputfile.write(output)
五、输出结果
六、结果分析
待分词文本:
欢迎大家来到文本计算与认知智能实验室
回溯路径是:
EMBEBEBSEBEBSSEBEB
倒序是:
BE/BE/S/S/BE/BE/S/BE/BE/BME
中文分词结果:
欢迎/大家/来/到/文本/计算/与/认知/智能/实验室
以上是关于HMM(隐马尔可夫)中文分词的主要内容,如果未能解决你的问题,请参考以下文章