一文搞定HMM（隐马尔可夫）

Posted 2021-09-04 ZSYL

HMM（隐马尔可夫）

• 学习目标
• 1. 自动机
• 2. 马尔可夫链和马尔可夫假设
• 3. 隐马尔可夫模型
• • 3.1 马尔科夫模型中的三个问题：
  • 3.2 似然度问题：
  • 3.3 解码问题
• 4. 案例
• • 4.1 如何对句子进行分词
  • 4.2 统计概率
  • 4.3 使用viterbi算法进行解码

学习目标

1. 知道什么是自动机
2. 知道什么是马尔可夫链
3. 知道隐马尔可夫是什么
4. 知道隐马尔可夫的原理是什么
5. 知道如何使用隐马尔可夫完成分词，词性标注等任务
6. 知道MEMM是什么
7. 知道CRF是什么

1. 自动机

自动机：（又称为 有限自动机，有限状态自动机，FSA）是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。

例如：

我们常用的正则表达式就是一种用来描述字符串出现字符的自动机。

假如我们有正则表达式：baa+!，表示的是ba后面有1个或这多个a，最后是一个感叹号。

我们可以把上述的自动机用图来展示，如下：

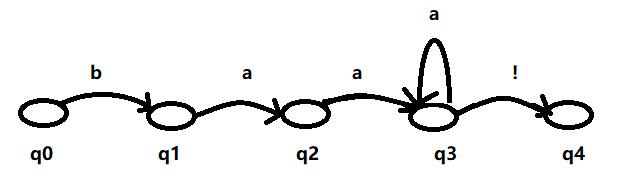
自动机从初始状态q0开始，反复进行下面的过程：找到第一个字母b，如果找到b那么进入到下一个状态，再去寻找下一个状态需要的字母，指导进行接收状态q4。

我们可以使用状态转移表来自动机：

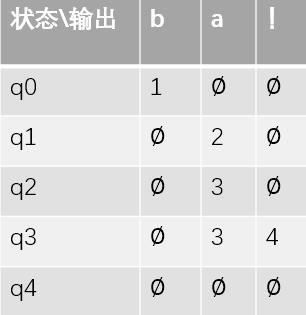
上述的状态机我们也称为确定的自动状态机DFSA(例如红绿灯)，如果位于q3的循环在q2上，那么在q2状态下，看到a，他是不清楚要向那个地方进行转移的。所以把这种状态机成为非确定的自动状态机 NFSA，（比如天气）。

2. 马尔可夫链和马尔可夫假设

马尔可链是自动状态机的扩展版，是一种带权的自动状态机。权重在马尔可夫链中就是连接弧的概率。离开一个节点的所有的概率和为1。

用马尔可夫链描述天气的变化，如果使用图模型来描述的话，可以有下面的示例：

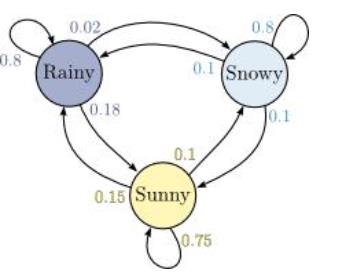
如果今天下雨，那么明天的天气会怎么样呢？

明天下雪的概率：0.02

明天下雨的概率：0.8

明天晴天的概率：0.18

上述的过程包含了概率上的一个重要假设：在一个一阶马尔可夫链中，一个特定状态的概率只和他的前一个状态是有关的：

马尔可夫假设：
$$P(q_i|q_{i-1}\cdots q_1)=P(q_i|q_{i-1})$$
如果是把马尔可夫应用于NLP的文本序列，那么他表示的就是二元N-gram模型

3. 隐马尔可夫模型

当我们要计算我们能够观察到的事件序列的概率的时候，马尔可夫链是很有用的。但是在很多情况下，我们感兴趣的概率是没有办法直接计算的。例如在词性标注的问题中，我们能够看到句子中的词，能够计算这个句子组合的概率。但是我们的目标是或者这个句子对应的词性的序列。这些词性序列是隐藏的，不能够直接被观察到，我们需要去推断隐藏的状态，这个时候我们就需要使用隐马尔科夫模型（HMM）。

隐马尔可夫模型可以使用以下内容来进行描述：

$Q=q_1,q_2,\cdots q_N$ 状态N的集合

$A=a_{11},a_{12}，\cdots ,a_{nn}$ 转移概率矩阵A。每一个转移概率$a_{ij}$表示从状态i转移到状态j的概率，同时从某一个状态出发的转移概率和为1

$O=O_1,O_2\cdots O_n$ 观察到的序列T

$B=b_i(O_i)$ 观察似然度，也叫做发射概率，表示从状态i得到观察$O_i$的概率

q_0,q_F 表示初始状态和终结状态

隐马尔可夫模型中，除了马尔可夫假设之外，还有另外一个假设，即输出独立性假设，即:

一个输出观察$O_i$的概率只和产生该观察的状态$q_i$有关
$$P(O_i|q_1,q_2\cdots q_T，O_1,O_2\cdots O_T)=P(O_i|q_i)$$

在类似词性标注的问题中，我们需要做的事情，在含有n个单词的观察序列的所有可能的隐藏序列中找到一个概率最大的隐藏序列，写成公式如下(其中帽子符号$\hat{}$表示对正确序列的估计)：
$${\hat{t}}_n={\mathrm{argmax}}_{t_n}P(t_n|w_n)$$

根据前面的两个概率假设，上述公式也可以写为：

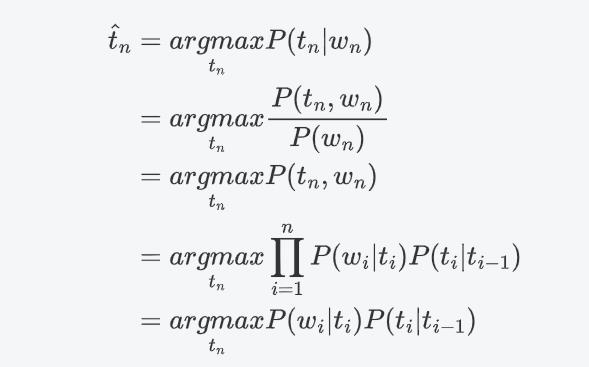
上述的公式中包含两个概率：

1. 标记的 转移概率：$P(t_i|t_{i-1})$

2. 单词的似然度(likelihood):又称为发射概率，即在状态$t_i$的情况下发现观测值为$w_i$的概率。

   似然度：likelihood的中文翻译，表示可能性、概率的意思

转移概率的计算方法：通过极大似然估计(MLE)，通过现有的语料，直接计算即可：

即：状态从$t_{i-1}到t_i$的总数 除以$t_{i-1}$的总数
$$P(t_i|t_{i-1})=\frac{C(t_{i-1},t_i)}{C(t_{i-1})}$$

极大似然估计：是一种概率在统计学中的应用，是一种参数估计方法，说的是说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，使用实验得出的概率作为样本的概率。

似然度概率的计算方法同理：
$$P(w_i|t_i)=\frac{C(t_i,w_i)}{C(t_i)}$$
即数据集中所有的$w_i为t_i$的样本数量 除以 该状态$t_{机器学习算法之——隐马尔可夫模型(Hidden\; Markov\; Models,HMM)\; 代码实现}$

隐马尔科夫模型（HMM）

HMM（隐马尔可夫模型）

02 隐马尔可夫模型 - HMM的三个问题 - 概率计算问题

HMM（隐马尔可夫）中文分词

隐马尔可夫（HMM）模型