时间序列分析：时间序列基本概念

Posted 2021-05-02 SAS知识

本文首先介绍时间序列的基本概念之常见平稳和非平稳模型，最后介绍SAS时间序列分析软件。

常见平稳和非平稳模型

前面说过，时间序列是随机过程的一个现实。我们对时间序列进行分析，就是希望根据时间序列的特征，找到可以刻画这个时间序列的随机过程。

接下来，将介绍描述时间序列的一类重要随机模型：平稳模型。平稳模型会假设随机过程保持概率特征上的统计均衡，其均值和方差不随时间而改变，即变化都是在一个固定的均值水平上，具有固定的方差。这类模型非常适合用来对平稳时间序列进行刻画。

1. 算子

为了便于对平稳模型和非平稳模型进行介绍，

2. 自回归模型

在描述某类实际中出现的时间序列时，一种特别有用的随机模型是自回归模型。在该模型中，随机过程的当前值被表达为由有限的过程先前值的线性组合和一个干扰（白噪声）构成，其形式如下：

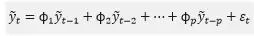
该等式表示的随机过程称为p阶自回归过程，简称AR（p）过程，其中，，为时间序列的均值。称其为自回归是因为这是从线性回归中发展而来的，但是，这里不再是用x预测y，而是用y自身的历史值来预测y，也称AR模型。如果引入后移算子B，那么由上面的等式可以很容易地推导出p阶自回归算子

，

从而，p阶AR模型就可以简记为

需要特别说明的是，1阶AR模型，记为AR（1），也可以表示为

考虑简单的1阶AR模型，经过m次替换后，即令，在右边可以得到

（1）自相关函数

由特征方程根的性质，可知一个平稳的自回归过程的自相关函数的变化趋势是由指数衰减和正弦波振荡衰减构成的。这是我们根据自相关函数判断序列平稳性的理论基础。

（2）自回归参数的表示

（3）偏自相关函数

在分析一个时间序列时，最初我们可能不知道适合于观测序列的AR过程的具体阶数，即p的取值，要采用类似于在多元回归中的方法去确定自变量的个数。其实，这时可以参考偏自相关函数。

偏自相关函数是基于以下事实的一种描述手段：只要一个AR（p）过程具有无限延生的自相关函数，那么，就可有自相关函数的p个非零函数来描述自身的特性。若用表示k阶差分方程回归表达式中的第j个系数，就是最后一个系数。由此可得到Yule-Walker方程，记为

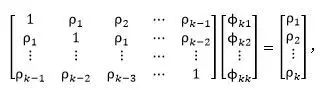
对k=1，2，3，…，依次求解方程，可以得到

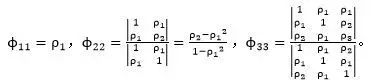
对于任何平稳过程，都可以由上述Yule-Walker方程定义偏自相关函数，当然也都是作为过程自相关函数pk的函数。并且，对于AR（p）过程，对于所有的k>p，有=0，该特征均适合于描述p阶AR过程。

因此，在求偏自相关函数的估计时，可以顺次拟合阶数为1，2，3，…的自回归方程，在每阶段的拟合中挑出最后一个系数，得到估计…。

Quenouille证明了：在p阶AR过程的假设之下，阶数大于或者等于p+1的偏自相关估计值近似服从均值为零、方差为1/n的独立正态分布，其中n为观测个数。这一论断可以作为判断AR模型阶数p的取值依据之一。

3. 移动平均模型

（1）自相关函数

可以看到，对于MA（q）的过程，当延迟阶数超过q时，过程的自相关函数为0。换言之，移动平均过程的自相关函数具有超出q步延迟的截尾性。

（2）移动平均参数的表示

由上述自相关函数的推导结果可知，若为已知，则由q个方程就可以解出参数，然而，与自回归过程线性的Yule-Wallker方程不同，这里的q个方程为非线性方程。除了q=1的简单情形，其余情形只能用迭代法求解。

（3）偏自相关函数

对于高阶的MA过程，偏自相关函数的严格表达式是很复杂的，但是可以证明偏自相关函数被衰减指数和（或）衰减正弦波控制。

（4）自回归过程和移动平均过程的对偶性

平稳的AR过程具有在某阶之后全为零的偏自相关函数，但是它的自相关函数是无限延伸的，且由衰减指数或衰减正弦波混合生成；相反的，有限的MA过程具有在某阶之后全为零的自相关函数，但由于它等价于一个无限的AR过程，因此其偏自相关函数将无限延伸，且被衰减指数和（或）衰减正弦波控制。

4. 自回归移动平均模型

为了在实际拟合时间序列时有更大的灵活性，有时会将自回归项和移动平均项一起纳入模型，这就引出了自回归移动平均模型（ARMA）：

际中，为了描述一个实际发生的平稳时间序列，往往能够得到自回归、移动平均，或者二者混合的模型，其中p和q的值不大于2，或者常常是小于2的。

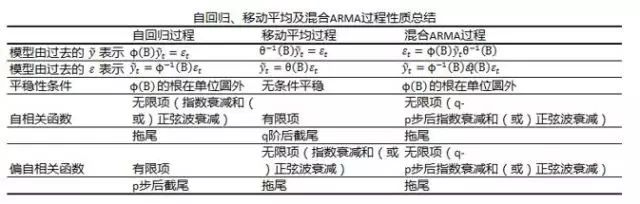
表17.1是针对自回归、移动平均及混合ARMA过程性质的总结。

表17.1 自回归、移动平均及混合ARMA过程性质总结

5. 非平稳模型

            在工商业中，常会遇到许多序列（如股票价格）都表现出了非平稳的特性，比如说不围绕一个固定的均值变化。然而这样的序列可能会表现出某种相同的特征，具体来说，虽然这些波动的总体水平在不同时间里其表现是不同的，但是在允许水平有差异的前提下，这些序列的其他广义特征可能是相似的。有些情况下，某种序列在经过一阶或者多阶向后差分后可以转换为平稳时间序列。

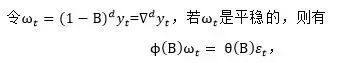
也就是说，描述具有该种同质非平稳特征的模型可以表示为

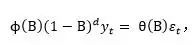
在实际应用中，d通常是0或1，或者最多是2。当d=0时与平稳特征相一致。

对于高阶d也可以定义同样的计算。因此，一般的自回归求和移动平均过程（ARIMA）就是对平稳过程作d次求和而生成的。后面将描述如何使用上述模型的一个具体形式来表达非平稳时间序列。

SAS时间序列分析软件简介

在SAS系统中，有四大模块可以用来进行时间序列分析：

• BASE SAS：利用第一篇中介绍的基本编程语言和时间序列的理论知识进行建模和预测。

• SAS/STAT：运用最小二乘法对历史数据或者残差进行回归。

• SAS/ETS：是SAS系统中专门进行时间序列预测的模块，提供了多种PROC步，对带有时间标识的序列进行处理、建模和预测。本章主要介绍运用该模块中的PROC步进行建模。

• SAS Forecast Server：是一种具有可扩展性的大型自动化预测解决方案，具有友好的图形用户界面（如图17.6所示），在较少人工干预的情况下，可快速自动生成大量高质量的统计模型，能自动选择最合适的统计模型，并生成预测。

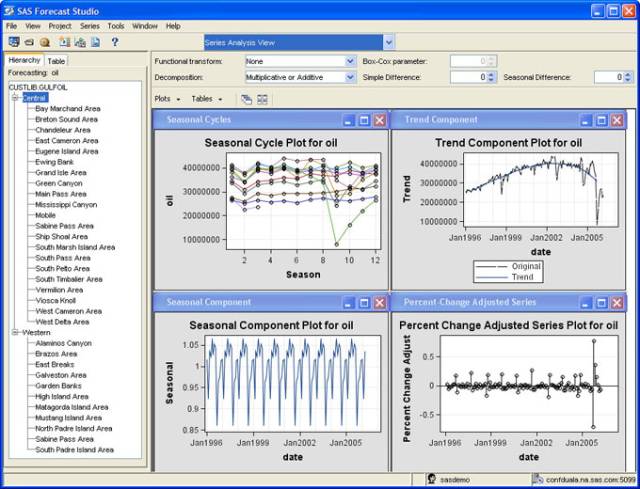
图17.6  SAS Forecast Server的用户界面

本文结束，下一篇文章介绍平稳时间序列分析。

回复【数据和代码】可以下载《深入解析SAS》一书的数据和代码。

查询往期文章，请回复下列关键字：

【安全】==>【SAS智能平台安全管理】系列文章

【Base基础】==>【Base SAS基础】系列文章

【编程概念】==>【SAS编程基本概念】系列文章

【描述性统计】==>【SAS统计分析系列：描述性统计分析】系列文章

【读外部数据】==>【读取外部数据到SAS数据集】系列文章

【假设检验】==>【参数估计与假设检验】系列文章

【单数据集处理】==>【单数据集处理】系列文章

【方差分析】==>【方差分析】系列文章

【主成分与因子分析】==>【主成分分析与因子分析】系列文章

【多数据集处理】==>【多数据集处理】系列文章

【线性回归】==>【线性回归】系列文章

【数据汇总展现】==>【数据汇总与展现】系列文章

小贴士

读者可以从以下链接获取SAS公司提供的免费版环境：

SAS大学版（SAS® University Edition）是SAS为在校大学生免费提供的基于虚拟机和网页的SAS环境。回复关键字【大学版】，可以查看详细介绍。

下载路径：

https://www.sas.com/en_us/software/university-edition/download-software.html

SAS学术版（SAS® OnDemand for Academics）是 SAS 为学术届人士免费提供的、在线的、基于SAS 私有云上的应用服务环境。

用户首先需要注册，然后按照提示信息就可登录。

注册路径：

http://odamid.oda.sas.com

本文转自《深入解析SAS — 数据处理、分析优化与商业应用 》

如若转载本文，请在文章顶部标注 “本文转自SAS知识 （ID: SASAdvisor），摘自《深入解析SAS — 数据处理、分析优化与商业应用 》”

作者介绍

夏坤庄

《深入解析SAS — 数据处理、分析优化与商业应用》第一作者， SAS软件研究开发（北京）有限公司客户职能部总监。在承担研发工作的同时，夏及其团队负责对SAS非英语市场提供技术支持，并且与在美国及其它地区的团队一起，服务于SAS的SaaS/RaaS业务，同时提供和验证关于SAS产品和技术在应用领域的最佳实践。在加入SAS软件研究开发（北京）有限公司之前，夏就职于SAS中国公司，历任资深咨询顾问、项目经理、首席顾问、咨询经理，拥有丰富的咨询和项目实施经验。在长期的从业经历中，不但为SAS的金融行业客户成功实施了众多深受好评的项目，而且在近年领导实施了非金融行业的多个大数据分析项目。

SAS知识    微信：SASAdvisor     长按二维码关注

欢迎大家投稿，一起分享SAS的点滴

投稿邮箱:  [e-mail]