一个令人惊艳的算法——布隆过滤器

Posted 2021-05-01 IT大咖说

概述

布隆过滤器(Bloom Filter)是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数，布隆过滤器可以用于检索一个元素是否在一个集合中。

如果想要判断一个元素是不是在一个集合里，一般想到的是将所有元素保存起来，然后通过比较确定。链表，树等等数据结构都是这种思路. 但是随着集合中元素的增加，我们需要的存储空间越来越大，检索速度也越来越慢(O(n),O(logn))。不过还有一种叫作散列表(又叫哈希表，Hash table)的数据结构，它可以通过一个Hash函数将一个元素映射成一个位阵列中的一个点，这样一来，我们只要看看这个点是不是1就可以知道集合中有没有它了。这就是布隆过滤器的基本思想。

算法

1、首先需要k个hash函数，每个函数可以把key散列成为1个整数；

2、初始化时，需要一个长度为n比特的数组，每个比特位初始化为0；

3、某个key加入集合时，用k个hash函数计算出k个散列值，并把数组中对应的比特位置为1；

4、判断某个key是否在集合时，用k个hash函数计算出k个散列值，并查询数组中对应的比特位，如果所有的比特位都是1，认为在集合中；

原理

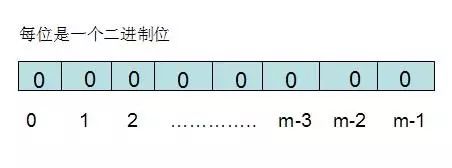
布隆过滤器需要的是一个位数组（这个和位图有点类似）和k个映射函数（和Hash表类似），在初始状态时，对于长度为m的位数组array，它的所有位都被置为0，如下图所示：

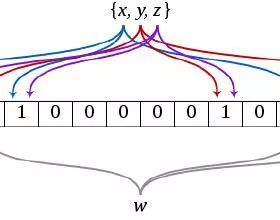
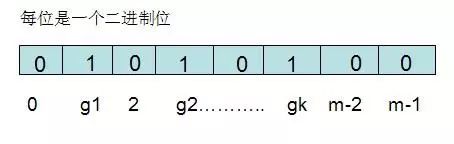
对于有n个元素的集合S={s1,s2......sn}，通过k个映射函数{f1,f2,......fk}，将集合S中的每个元素sj(1<=j<=n)映射为k个值{g1,g2......gk}，然后再将位数组array中相对应的array[g1],array[g2]......array[gk]置为1：

如果要查找某个元素item是否在S中，则通过映射函数{f1,f2.....fk}得到k个值{g1,g2.....gk}，然后再判断array[g1],array[g2]......array[gk]是否都为1，若全为1，则item在S中，否则item不在S中。这个就是布隆过滤器的实现原理。

布隆过滤器优点

它的优点是空间效率和查询时间都远远超过一般的算法，布隆过滤器存储空间和插入 / 查询时间都是常数O(k)。另外, 散列函数相互之间没有关系，方便由硬件并行实现。布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势。

布隆过滤器缺点

但是布隆过滤器的缺点和优点一样明显。误算率是其中之一。随着存入的元素数量增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣。

另外，一般情况下不能从布隆过滤器中删除元素. 我们很容易想到把位数组变成整数数组，每插入一个元素相应的计数器加 1, 这样删除元素时将计数器减掉就可以了。然而要保证安全地删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题

如何选择哈希函数个数和布隆过滤器长度

过小的布隆过滤器很快所有的 bit 位均为 1，那么查询任何值都会返回“可能存在”，起不到过滤的目的了。布隆过滤器的长度会直接影响误报率，布隆过滤器越长其误报率越小。

哈希函数的个数也需要权衡，个数越多则布隆过滤器 bit 位置位 1 的速度越快，且布隆过滤器的效率越低；但是如果太少的话，那我们的误报率会变高

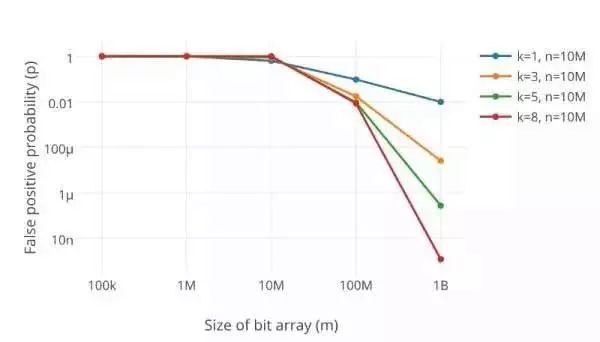
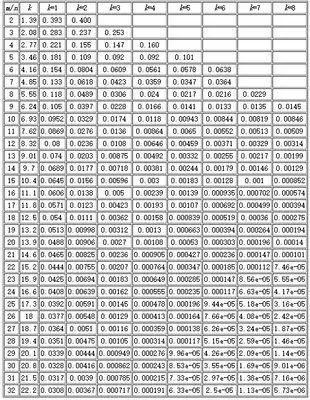
k 为哈希函数个数，m 为布隆过滤器长度，n 为插入的元素个数，p 为误报率。

应用场景

• HTTP缓存服务器、Web爬虫等

主要工作是判断一条URL是否在现有的URL集合之中（可以认为这里的数据量级上亿）。

对于HTTP缓存服务器，当本地局域网中的PC发起一条HTTP请求时，缓存服务器会先查看一下这个URL是否已经存在于缓存之中，如果存在的话就没有必要去原始的服务器拉取数据了，这样既能节省流量，还能加快访问速度，以提高用户体验。

对于Web爬虫，要判断当前正在处理的网页是否已经处理过了，同样需要当前URL是否存在于已经处理过的URL列表之中。

• 垃圾邮件过滤

Java实现布隆过滤器

先实现一个简单的布隆过滤器

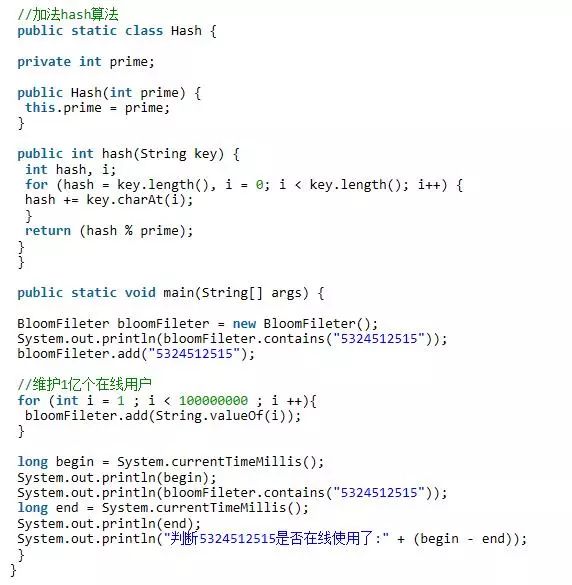
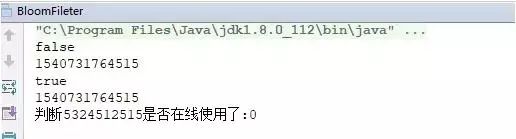
这段代码是构建了一个10亿位的bitSet，然后把一亿个userId加入到了我们的布隆过滤器中，最近判断5324512515这个userId是否登录，打出代码的执行时间

来都来了，走啥走，留个言呗~

 IT大咖说  |  关于版权 

感谢您对IT大咖说的热心支持！

相关推荐

推荐文章

• 
  

• 
  

最近活动

• 
  

  
  

点击【阅读原文】更多IT技术圈干货等你挖掘