水桶实验：牛顿与马赫

Posted 2023-01-24 卓晴

• Newton vs. Mach: The Bucket Experiment
• Kathy老师讲述的有趣科学历史

 

01 水桶实验

---

一、背景介绍

  It’s a debate that’s raged for millennia which aspects of our reality are absolute and which are merely relative. When it comes to the concept of motion two physicists held opposing views. And to resolve the differences in their philosophies they invoked a simple thought experiment that involved, well, a bucket and some water.

  But does this experiment really prove that motion has absolute meaning or does it actually demonstrate the opposite that motion is just a relative construct.

  Today we’ll pit these two thinkers against one another to find out. This is dialect with newton versus Mach, the bucket experiment.

二、绝对运动

  When newton introduced his groundbreaking theories in the late 1600s, he framed them against a mathematical background that contained three absolutes: time, space and motion. “Time, space and motion, the vulgar conceive these quantities only in their relation to sensible objects,” he wrote, “But absolute time flows uniformly without regard to anything external. Absolute space always remains similar and immovable. Absolute motion is the translation from one absolute place to another absolute place.”

  Although some were skeptical of these definitions, the success of newton’s theories in describing motion and gravity gave no real reason for physicists to question them over the following centuries. But in the late 1800s the skepticism of one physicist Rrnst Mach would have an irreversible impact on the course of physics. “… Newton has grown unfaithful to his resolve to investigate only actual facts.” Mach declared in his signature text, “The science of mechanics”. “The question whether emotion is in itself uniform is senseless …”

  “We reach our ideas through the interdependence of things upon one another…” In his ensuing critique of Newton, Mach declared that, " No one is competent to predicate things about absolute space or motion, that they are purely mental constructs." His ideas helped propel a young Albert Einstein towards the theory of relativity. And soon in the wake of relativity’s massive success, two of the three pillars of Newton’s absolutes time and space came crashing down.

  But today Newton’s final absolute motion still stands. That is all our modern theories of reality are framed against a mathematical background which posits one particular type of motion, acceleration as absolute. And although Mach was ahead of his time in realizing that both the ideas of absolute time and absolute space were soon to fall. His critique of newton’s concept of absolute motion never experienced similar validation.

  And so modern physicists have split into two camps. Those who believe Newton’s assertion about absolute motion to be correct. and those who believe Mach’s critiques will eventually come to fruition.

三、水桶实验

  Particularly what Mach found lacking about absolute motion was the experiment cited by newton to justify it, the bucket experiment. Newton had observed that if you took a bucket filled with water and started to spin it, the water inside would go from being flat to having a concave shape. According to Newton this difference proved motion was absolute. How exactly ? Well let’s break it down.

  Newton notes that there are exactly two points over the course of the experiment that the bucket and the water will be relatively at rest. The first point is before the bucket has been spun when both the bucket and the water aren’t moving. The second point is after the bucket has been spun, and its motion having been communicated to the water via friction. The water takes a concave shape. At this point both the bucket and the water are spinning at the same rate together, and from the perspective of an observer who is rotating along with them, the entire apparatus will appear to be at rest.

  Now according to Newton if the observer in the spinning frame didn’t already know the bucket was rotating, they could deduce it from the fact that the shape of the water is concave. Conversely if we had an observer who was rotating with respect to the still frame, so that relative to them the bucket and the flat water appeared to be spinning, they could deduce that the bucket was actually at rest by the flat shape of the water.

  Thus the first picture with the water in the bucket being flat represents absolute rest. While the second picture with the water being curved represents absolute motion. Distinctions such as these Newton argued always make it possible to distinguish between motion that is true or real and motion that is only apparent. But mock fired back that this argument was too abstract. The centrifugal forces which seemingly caused the water in the bucket to take its concave shape aren’t produced by an absolute rotation, he argued. but by a rotation relative to the mass of the earth and the other celestial bodies. Every statement about motion mock believed implicitly carries an abbreviated reference to the rest of the universe, and thus removing the rest of the universe from the picture, leaves us unable to define what we mean by motion in the first place.

  Both Newton and Mach seem to make compelling points. But who is ultimately right ? To resolve this metaphysical face-off, we’re gonna have to step into the rink and get our hands a little wetter with the bucket experiment.

四、第一回合：马赫获胜

  First let’s ask what actually gives the water its concave shape? Well, as our bucket begins to spin the water inside gets flung outwards towards the walls. With nowhere else to go this water is forced to rise. Gravity however keeps it from rising too much and as a result the surface of the spinning water achieves a rotational equilibrium. Next conservation of energy tells us that in this state of equilibrium the kinetic energy of a spinning ring of water at a distance r from the center of the bucket will be equal to its potential energy mgh. Since the velocity of the spinning ring is simply the angular velocity of the bucket times the rotation radius, we can see after a little algebra that the height of the ring of water is thus proportional to the square of its distance from the center of the bucket, meaning the overall shape of the water will be a parabola.

  But the height of the water is also dependent on another parameter. The strength of the nearby gravitational field g. And if we dial down the strength of that field to zero we see that the height of the water goes to infinity. What this implies is that spinning our bucket in zero gravity would actually result in all the water being ejected from the bucket. A fact which tells us something that Newton neglects to mention, that is that the concave shape of the water is not just a consequence of the bucket spinning, but rather a consequence of its spinning in the presence of a gravitational field.

  The implication, of course, is that in the absence of such a field the shape of the water’s surface no longer acts as an indicator of rotational motion. Of course one could contend that this doesn’t affect Newton’s argument. Since if we spun our bucket in zero gravity we’d have one picture of total rest and one picture where our water is flying all over the place. But Newton’s objective with the bucket experiment was not to demonstrate a case where motion and rest were easily differentiated, but rather to find a case where motion and rest appear essentially indistinguishable. And then show, that even in these instances such telltale differences can always still be found.

  The problem then is that, for the bucket experiment to fulfill this criteria,that is for there to be a state of rest for the system which is only apparent,the bucket is required to inhabit a gravitational field. Thus to make his case that true motion can always be locally distinguished. within a system. Newton is actually forced to invoke a nearby mass external to that system, meaning his experiment could not be reproduced in the absence of external matter. Since this falls more in line with Mach’s argument than it does with Newton’s, we’re crowning Mach the winner of this first round.

五、第二回合：牛顿获胜

  Likely realizing the bucket experiment was a little too contextual, Newton in his writings offers up a second experiment. Take two globes attached to a cord and spin them around in a circle about their center of mass. Then by investigating the tension produced in these chords one could determine the quantity and direction of the circular motion. Considered even in an immense vacuum where there was nothing external or sensible with which the globes could be compared.

  Now this experiment, unlike the bucket one, has the benefit of being able to be reproduced in the absence of external matter. But in keeping with the bucket experiment it offers two states of apparent rest along with a theoretical way to measure the difference between them. To see how this measurement could occur it might be easier for us to envision our two masses as attached by a spring rather than a cord. As the masses rotate centrifugal forces push them outwards stretching the spring. A stretched spring therefore indicates absolute rotation, and by measuring how much the spring has stretched one can determine the exact magnitude of force causing the rotation.

  With this simple definitive seeming argument Newton claims the title as our second round winner. Establishing a concept of absolute motion that could be empirically verified even in the absence of all other matter in the universe.

六、第三回合：突然死亡决一胜负

  Who wins the final round ? Well, to find out we need to think about what the bucket experiment is really saying. Let’s recall again that Newton’s original argument relied on there being two distinct points of view of relative rest. One in which the bucket and water are at rest with respect to one another, and the water is flat. And one in which the bucket and water are at rest with respect to one another but the water is curved.

  Similarly for the masses attached to the spring in a vacuum in both pictures, the masses and the spring are at rest with respect to one another. But in one picture the spring is stretched, and in the other it isn’t. Now the picture of the stretched spring is supposed to correspond to absolute motion. But we also have to recall the fact that the observers in these frames don’t know whether they’re spinning or not. And therefore don’t have access to information from the outside that would indicate to them prior to their measurements made inside their frame whether or not their frame is inertial.

  Let’s say that besides the spring is a rod of much stiffer material with markings along it to indicate the length between coils of the spring. The observer can then read the markings to measure the length between coils, and thereby determine how much the spring has stretched. The question then becomes how does the observer know whether the measurement they make corresponds to the shortest possible length of the spring or not.

  For in rotational frames only the shortest possible length of the spring or its natural resting length indicates absolute rest. Every other length indicates varying amounts of rotation.

  In the bucket experiment only flat water could indicate absolute rest. But here the problem is trickier. Here the observer has to know prior to making any measurements in their frame what length corresponds to the natural undeformed state of the spring, and to know that the observer would have had to previously have calibrated their spring rod measuring device in a frame that was already known to be inertial.
  such as in a laboratory back on earth.

  Only by measuring the resting length of the spring at a time and place when they were certain there were no external forces at work stretching or compressing the spring could an observer ascertain what picture of the spring corresponds to absolute rest. Thus even in the empty universe version of Newton’s experiment observers would still have to import information from inertial frames that existed elsewhere in order to draw any conclusions about the state of their motion. That means in one way or another an observer has to reference an external environment no matter how distant or removed this environment is.

  Knowledge of the local system cannot ultimately be untangled from the greater environment. So what does this mean for Newton’s argument ? Well it means the globes and chord experiment does not actually meet the criteria for which Newton devised it, the criteria of reproducibility in an empty universe. And because of that it falls short of proving absolute motion in the same way the bucket experiment fell short. It relies on the presence of an external system in order to demonstrate absolute motion. And well at least to us this seems most in keeping with Mach’s assertion that all our principles of mechanics are experimental knowledge concerning the relative positions and motions of bodies.

  Now were we to expand Newton’s argument to allow observers in our rotating systems to retain a memory of how substances and materials behaved in inertial systems elsewhere. Then clearly his case still stands. And to some degree this must have been Newton’s reasoning. Because obviously an observer who doesn’t know anything about how buckets or water work wouldn’t be able to draw any conclusions about the state of their motion from the bucket experiment either.

  But Newton clearly also wanted to prove knowledge of absolute motion was a localized phenomenon, which would always reveal itself under careful enough isolated scrutiny. Yet if you allow your observers enough memory, memory of how, say, springs buckets cords and water behave elsewhere in other systems at other times, this is equivalent to expanding the system of reference beyond a spatio-temporally localized point of view. Thus Newton can’t have it both ways.

  Knowledge of absolute motion can’t both be always discernable and always localized. One of the two has to go. But if we try to preserve localization at the cost of memory this means observers could potentially disagree on their states of motion with no empirical experiment able to differentiate between them.

  On the other hand, if we try to preserve discernibility and require that motion must always be empirically verifiable, we have to invoke memory sufficient enough to reference a greater collective of systems.

  Essentially this leaves us with two primary resolutions to the bucket experiment . One. absolute motion is real and localized. But knowledge of it is not always possible. This is equivalent to saying that although observers may potentially disagree on who is or isn’t moving motion is still real and governs how our universe works. This would however make absolute motion an unobservable phenomenon, something which physics and science in general tends to disfavor. Two. What we perceive as absolute motion is actually an emergent property of a network of systems that cannot fundamentally be isolated from one another, meaning motion at some level must ultimately be relative.

  So which of these answers is it ? Does absolute motion have real meaning outside our mathematical descriptions ? Or is it simply a poorly defined concept ? A relic of dogmatic belief that like absolute space or absolute time needs to be fundamentally re-examined.

  Well for the time being it’s up to you to decide. So let us know what you think in the comments because until next time this has been dialect.

  Thanks for watching.

 

02 机械运动相对性

---

• Newton vs. Mach: The Bucket Experiment

一、背景介绍

  这是一场持续了几千年的争论，我们现实世界的哪些方面是绝对的，哪些是相对的。 】】当这个争论涉及到机械运动概念时，有两位物理学家持有相反的观点，他们俩一位是艾萨克·牛顿，另一位是恩斯特·马赫。 】】他们为了解决理念差异，进行一个简单的思想实验，其中涉及一个水桶和一些水。

▲ 图2.1.1 艾萨克·牛顿与恩斯特·马赫

  但是这个实验是否真的证明了运动具有绝对意义，或者只是相对的。今天，Dialect 通过短片展示这两位思想家之间的相互较量，以便找出答案。 】】

▲ 图2.1.2 水桶实验

二、绝对运动

  当牛顿在 17世纪后期提出他的开创性理论时，他将理论置于具有三个绝对物理量的数学基础之上。 】】这三个物理量分别是时间、空间和运动。】】他在《自然哲学之数学原理》的著作中，开宗明义写到： “…时间、空间和运动，普通人只在它们与可感知对象的关系中理解这些量，但绝对时间均匀流动，不考虑任何外部事物。绝对空间始终保持一致和不动。绝对运动是从 一个绝对的地方到另一个绝对的地方。” 】】 在他的理论中，这三个物理量分别各自独立、绝对存在着。

▲ 图2.2.1 牛顿理论的三个绝对量

  这么绝对、这么武断，自然就会遭到一些人的怀疑，但谁承想牛顿理论在描述运动和引力方面是那么的成功，所以在接下来的几个世纪中，那些怀疑这些绝对物理量的人没有找到攻击的真正把柄。 】】时光荏苒，到了十九世纪后期，一位物理学家恩斯特·马赫 (Ernst Mach) 对牛顿绝对时空发起来挑战，并对牛顿的绝对时空观理论通了一个大窟窿。 】】马赫在其著作《力学科学》中毫不客气的评价牛顿： “……牛顿已经背叛了他只研究真实世界的初心， 他关于机械运动的基本概念本身是否一致都没有下功夫搞搞清楚。理论思想是基于这些相互循环定义的概念之上…”

▲ 图2.2.2 通过一些相互依存的概念来发展我们的思想

  在随后对牛顿的批评中马赫宣称，“没有人有能力关于绝对空间或绝对运动事物下断言，这些概念纯粹只是从内心中构造出来的。” 】】正是受到马赫的批判思想的影响，年轻的阿尔伯特·爱因斯坦提出相对论。 】】同样牛X的相对论取得巨大成功，之后不久，牛顿绝对时空的三大支柱中的两个就崩塌了， 即绝对空间与绝对时间消失了。今天只剩下牛顿的绝对运动仍然坚挺。

▲ 图2.2.3 牛顿绝对物理量中的前两个崩塌了

  请注意这里讨论的绝对运动不是指匀速直线运动，而是具有加速度的运动。这种绝对的加速度的理念成为现代关于现实世界的物理理论基石。 】】马赫对牛顿绝对时空的批判思想领先于所在的时代，在其之后人们逐渐抛弃了绝对时间和绝对空间的概念，但对牛顿绝对运动概念的批判却进展缓慢。】】对此现代物理学家分成了两个阵营： 一个阵营是相信牛顿关于绝对运动断言是正确的教条主义者，另一阵营是相信马赫批评结论的实证主义者。

▲ 图2.2.4 物理阵营分成两个学派

三、水桶实验

  实际上对有可能会碰上马赫关于绝对运动的批判，牛顿早就有所准备。 为此他设计了一个思想实验来证明绝对运动的存在，这个实验使得物理阵营分成两个学派。】】牛顿观察到，如果你拿一个装满水的桶并开始旋转它，里面随之旋转的水的表面就会从平的变成凹形的。 】】根据牛顿的说法，这种差异证明了运动是绝对的。 】】真的可以证明吗？ 好吧，让我们深入了解一下。

▲ 图2.3.1 牛顿的水桶实验

  牛顿指出，在整个实验过程中，水桶和水能够保持相对静止的情况有两种。 】】第一种情况是在水桶和水都没有旋转，保持静止。 此时水面呈现平面形状。】】 第二种情况是水桶旋转之后，通过摩擦把运动传递给水，最终水桶和水一起以相同的速度旋转，此时水面呈现凹面形状。】】如果从一个围绕水桶以相同速度旋转的观察者角度来看，整个水桶似乎处于静止状态。

▲ 图2.3.2 与水桶一同旋转的观察者看到水桶和水也是静止的

  现在根据牛顿的说法，如果与水桶一同旋转的观察者事先不知道他和水桶在旋转，但他可以从水的形状是凹的这一事实中推断出他们在旋转。 】】相反，如果一个观察者相对一个静置水桶进行旋转，他看到的水桶和里面的水似乎在旋转，但他可以根据水的平面形状推断出水桶实际上是静止的。

▲ 图2.3.3 相对静置水桶旋转的观察者看到的水平面是平的

  将这两种情况绘制如下两张图形。第一张桶里的水面是平的图片代表绝对的静止， 第二张水面弯曲的图片代表绝对运动。】】根据牛顿所论证的说法，可以区分真实的运动和只是表面上的运动。

  对此马赫不服，他说牛顿粗枝大叶的论证太简陋了。 使得桶中的水面呈凹形不仅仅是旋转产生离心力的作用结果， 还包括地球以及其他天体质量所产生的的万有引力的作用。 】】 所以这个旋转水桶实验应该包含有水桶、地球以及所有其它天体之间的相对运动。 】】因此牛顿定义的旋转运动还隐含了对宇宙其余部分的参考。 但牛顿在论证中删除了宇宙的其余部分，从而使得我们对运动定义犯迷糊。

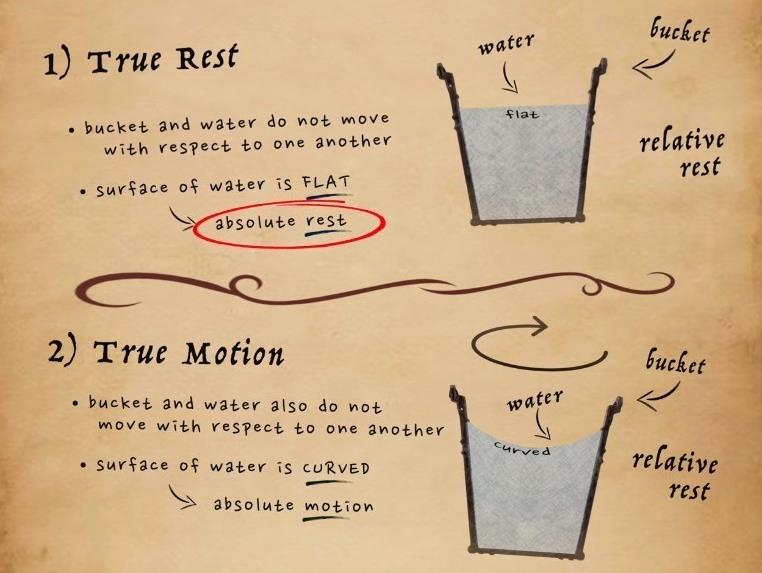
▲ 图2.3.4 水桶中的水面代表这绝对静止与绝对旋转

  至此牛顿和马赫似乎都提出了令人信服的观点。 但最终谁是对的？ 】】为了解决他两人之间形而上学的对峙，我们将不得不走进他们水桶辩论场，来试试其中的水到底有多深。

▲ 图2.3.5 马赫与牛顿的观点究竟谁是正确的呢？

四、马赫获胜

  首先探究一下什么使得水面呈现凹形？ 】】好吧，当水桶开始旋转时，随之旋转的水由于离心力会向外冲向筒壁，碰壁的水无处可去，只好被迫上涨。】】 然而重力阻止它上升太多，最终水的表面达到旋转平衡。 】】利用能量守恒定律可知，在这种平衡状态下距离水桶中心 r 处的一圈旋转水动能’将等于其势能 m·g·h。】】 由于旋转水环的速度就是水桶的角速度乘以旋转半径 r，经过代数运算可以看出水环的高度与其到水桶中心的距离的平方成正比 ，】】这意味着水的表面形状是抛物线。

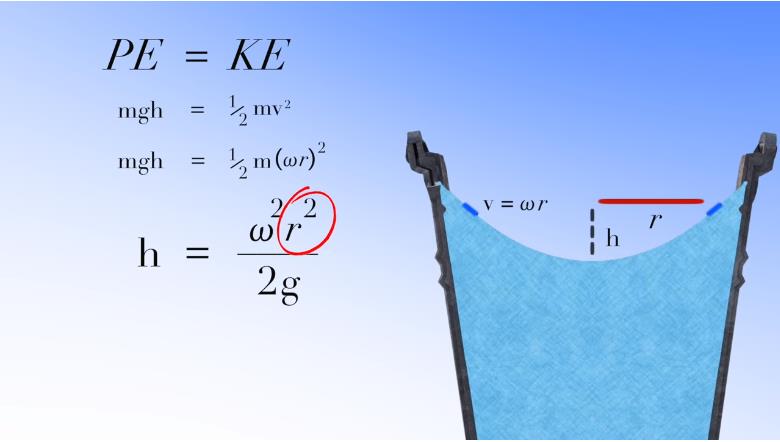
▲ 图2.4.1 旋转水面切面是一条抛物线

   大家可以看到在水面方程中还有一个参数， 那就是附近引力场的强度g。】】 如果将该场的强度逐步降低至零，水的高度将趋于无穷大。 】】这意味着在零重力下旋转水桶会导致所有的水从水桶中喷出。】】通过分析可以知道，牛顿水桶实验中提到旋转的桶和水保持相对静止，水面呈现凹形的情况不仅仅是水桶旋转的结果，还包括它所在的引力场的作用结果。

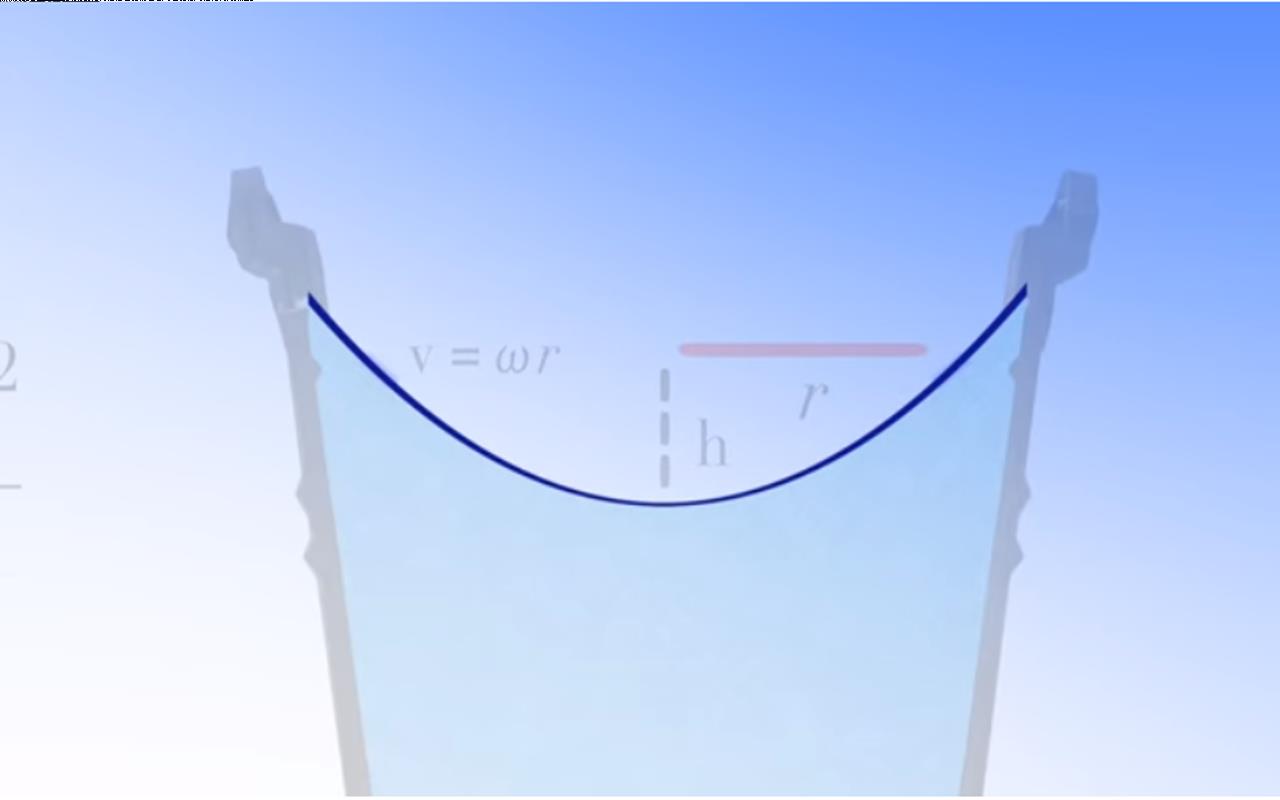
▲ 图2.4.2 在无重力情况下，旋转的水桶将不会存在水面

  这意味着在没有重力场的情况下，水面的形状不能作为旋转运动的指示器。 】】当然，有人会说这不会影响牛顿的论证。 】】因为如果在零重力下旋转水桶，将会有两种情况，一种是完全静止的景象，一种是水到处飞溅的景象。】】 但是牛顿进行水桶实验的目的不是要证明运动和静止截然不同的情形，而是要找到运动和静止看起来无法区分的情况，】】即找到表面上看起来是旋转或者表面上看起来是静止的情况，然后论证这些情况下依然可以找到它们之间的差异。

▲ 图2.4.3 无重力下只有两种情况发生

  那么问题来了，为了让水桶实验满足这个标准，即水桶表面看起来是静止的，只有了重力场中才行。 】】这样才可以通过局部观察水面的形状来区分静止还是运动。】】牛顿的水桶思想实验必须要用到外部的重力场，这意味着他的实验无法在没有外部其它天体的情况下重现。】】

  论证到此，你是否看出这更符合马赫提出的反对绝对运动观点，而不是牛顿绝对运动论点。】】 所以这轮关于水桶实验的辩论，马赫胜出。

▲ 图2.4.4 关于水桶思想实验，马赫胜出

五、旋转小球

  功力深厚的牛顿可能意识到水桶实验的确需要依赖于重力场，他在著作中于是给出了第二个实验，旋转小球实验。】】 将两个球体通过一根绳子相连，然后围绕它们质心旋转。通过研究绳子中产生的张力，可以确定旋转的大小和方向。】】 这个实验就可以在没有引力场的真空中进行啦，不需要有任何其它外在物体或者引力场作为参考。

▲ 图2.5.1 旋转小球实验

  这个实验与水桶实验的确不同，它可以在没有外部其它物体或引力场的情况下复现实验结果。 】】但为了与水桶实验保持一致，它提供了两种表面看起来都是静止情形，以及一种测量它们之间差异的理论方法。】】 要理解这种测量原理，我们将连接两个质量球体的绳索更换成弹簧。 】】当球体旋转时离心力将它们向外推，从而拉伸弹簧。 所以变长的弹簧表示存在绝对旋转。通过测量弹簧拉伸的程度，可以确定旋转的大小。

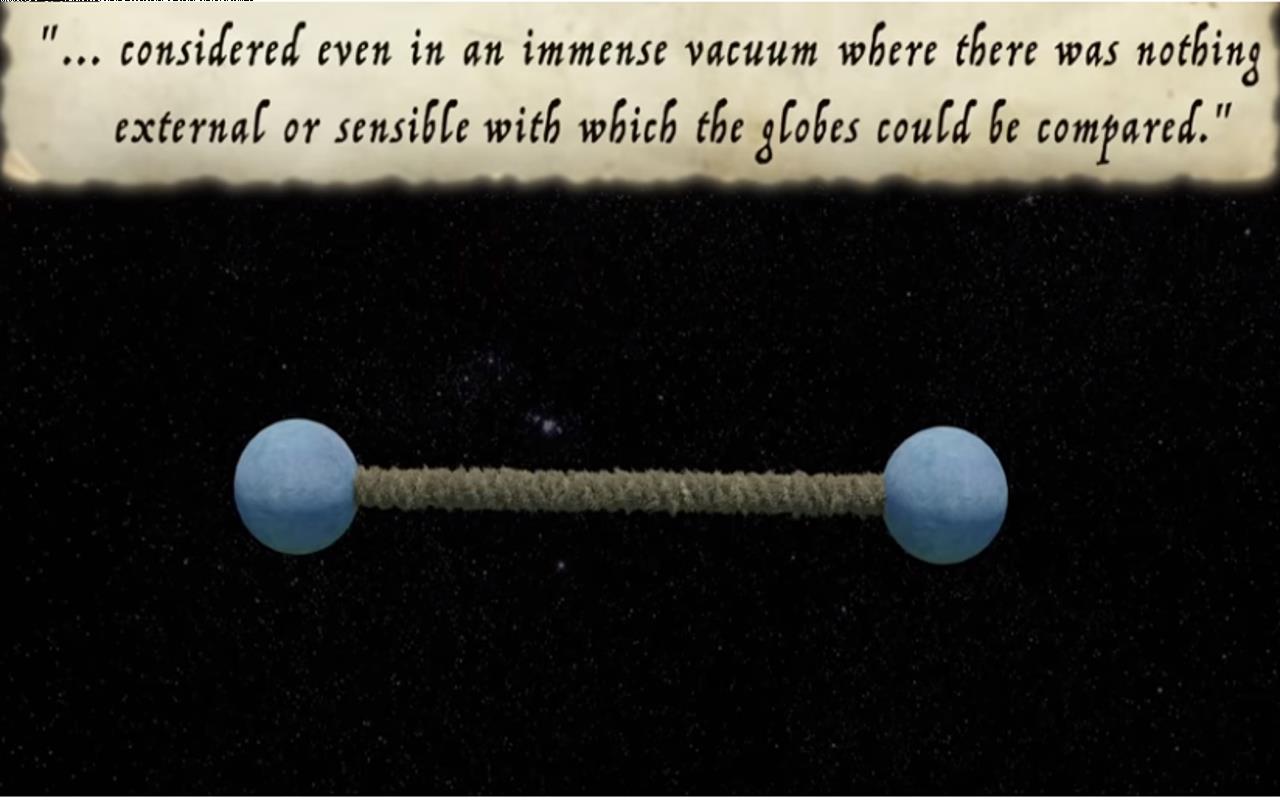
▲ 图2.5.2 通过测量连接弹簧的拉伸确定是否具有绝对旋转

   通过这个同样简单的思想实验，牛顿的绝对运动的观念再次战胜了马赫。】】因为它可以在宇宙中没有其他物体的情况下通过测量验证绝对运动。

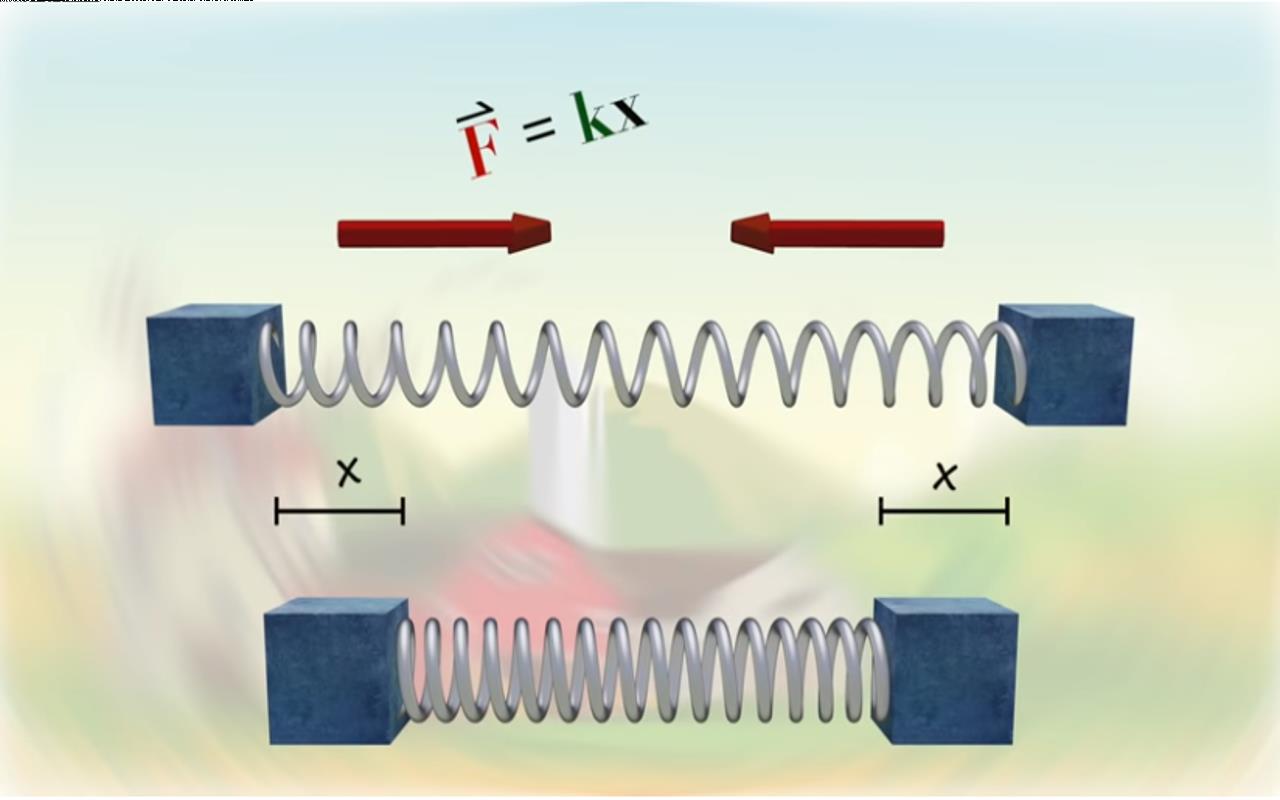
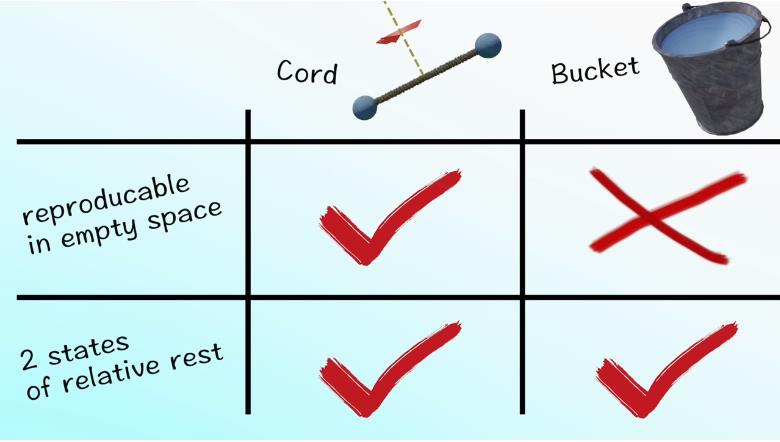
▲ 图2.5.3 旋转小球实验满足绝对运动的假设

六、决一胜负

  那么牛顿和马赫谁能赢得最后一轮呢？ 好吧，要找出答案，我们需要重新考虑桶实验的真正含义。 】】让我们再次回顾一下，牛顿最初的水桶实验依赖于相对静止的两种截然不同的观点。】】 一种是桶和水相对静止，水是平的； 还有一个桶和水相对静止，水是弯曲的。】】类似地，牛顿第二个思想实验是通过弹簧连接的两个质量块，质量和弹簧相对于彼此处于静止状态的两个状态：】】 一个状态是弹簧被拉长了，而 另一个状态弹簧没有被拉长，拉伸弹簧的状态应该对应于绝对运动。

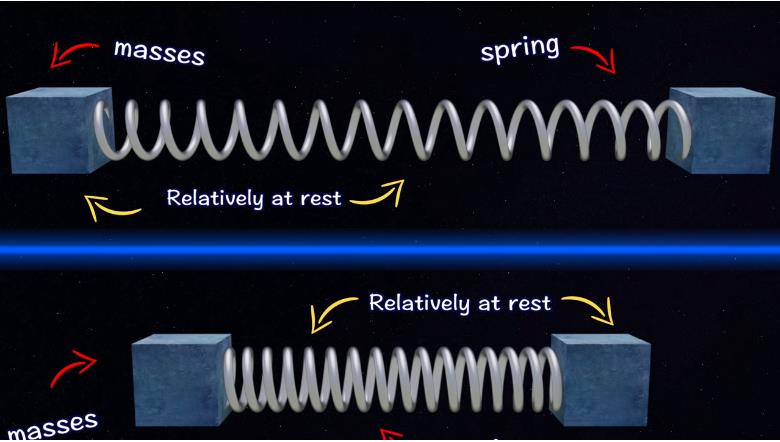
▲ 图2.6.1 上面两个状态表明运动和静止两个状态

  但我们也必须记住这样一个事实，即这些实验中的观察者不知道他们是否在旋转，也无法从外部获得额外的信息。】】所有结论只能依靠实验环境内根据观察结果判断是否是静止还是运动。】】

  假设除了弹簧之外，还有一根由硬材料制成的直尺，尺子上带有标记以指示弹簧长度。 】】然后观察者可以读取直尺来测量弹簧长度，从而确定弹簧拉伸了多少。】】 那么问题就变成了观察者如何知道他所做的测量是否对应于弹簧的最短长度。

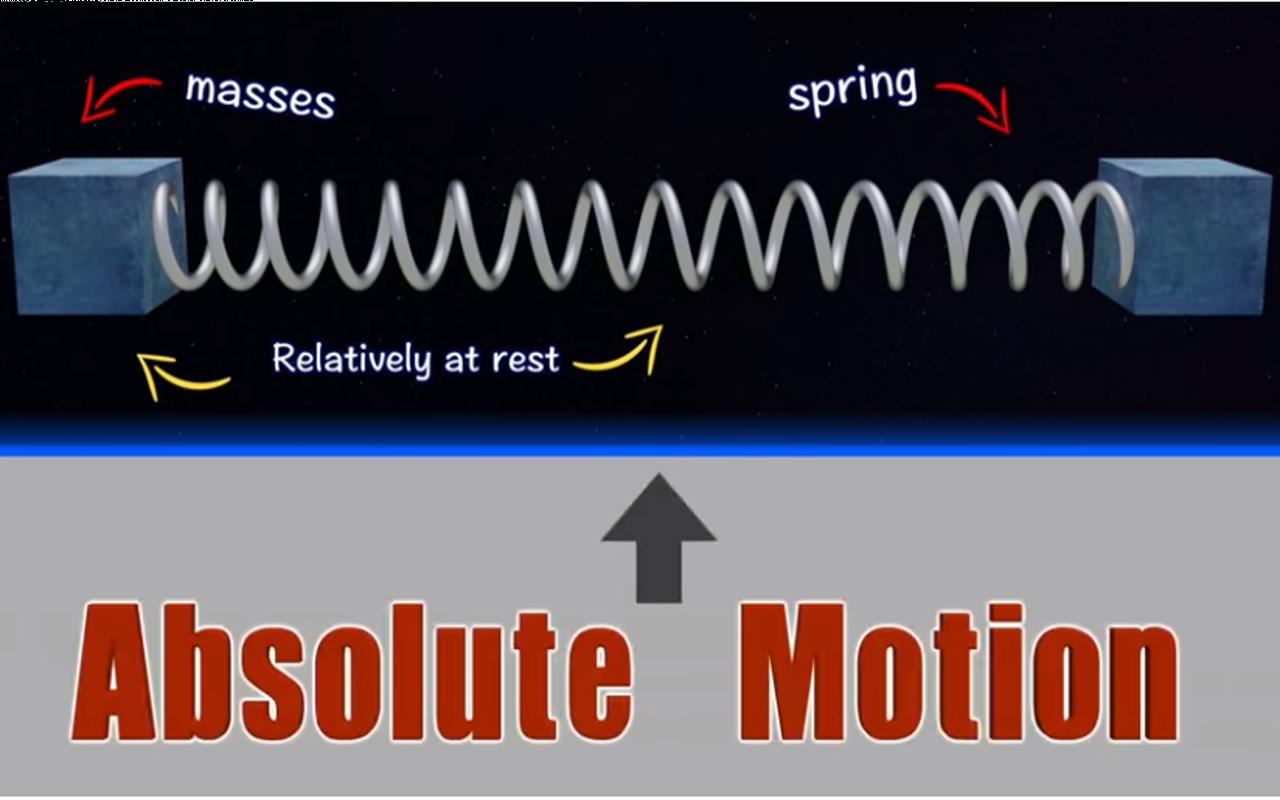
▲ 图2.6.2 如何确定弹簧长度是最短的可能长度呢？

  对于旋转弹簧和质量块的实验，只有弹簧达到最短长度或其自然静止长度才表示绝对静止， 】】其他不同长度表示不同的旋转量。】】

  在水桶实验中，平坦的水面状态就能表示绝对静止，】】但质量块弹簧实验中的问题更棘手，因为观察者必须知道什么长度对应于弹簧的未变形状态，】】这要求观察者必须事先在已经存在的惯性坐标系中测量实验中的弹簧，比如在地球上的实验室里。】】只有在他们确定没有外力作用时弹簧上的静止长度，观察者才能确定现在观察到的质量块与弹簧是否对应绝对静止。 】】在没有其它天体作为参考的真空中，观察者仍然必须从其他地方的惯性系中输入信息，以便得出关于弹簧运动状态结论。】】 这意味着观察者必须以某种方式参考外部环境信息，无论有多远或多久。所以系统局部信息最终还是与更大的外部环境纠缠在一起。

▲ 图2.6.4 旋转弹簧小球实验需要从惯性系中获得弹簧最短信息

  那么这对牛顿的论证意味着什么呢？ 这意味着旋转质量块弹簧实验实际上并不符合牛顿设计的标准，即在空无一物的宇宙中能够复现实验结果。】】 正因为如此，它与水桶实验一样无法证明绝对运动的存在。 它依赖于外部环境信息来验证绝对运动。 】】这似乎更加符合马赫的断言，即我们所有的力学原理都是关于物体相对位置和运动的实验知识。】】至此，牛顿理论中的三个绝对物理量都被推翻了吗？

七、先验知识

  为了挽回牛顿的面子，我们需要扩展牛顿的论点，让旋转系统中的观察者能够记住实验中的材料在其他惯性系统中的特性。 】】在此条件下，牛顿的绝对运动理论又可以站得住脚了。 实际上，这种扩展论点牛顿也是承认的。 】】他的著作中给出了一个实验观察者的资质要求，就是观察者应该具有一些先验的，或者不证自明的知识。】】你想想，如果一个人对水桶或水的特性一无所知， 那么他也无法从水桶实验中得出关于水桶运动状态的任何结论。

▲ 图2.7.1 牛顿理论中关于实验观察者的假设推论

   但我们知道牛顿内心是想证明绝对运动可以根据局部现象进行判断，一个观察者不需要其它额外的信息，会在充分仔细观察下判断物体是否运动。】】 然而，如果你允许观察者有丰富的知识，比如弹簧、水桶、绳索和水在其它时间其它系统中的表现，这相当于将参考系统扩展到局部时空之外。 】】所以牛顿的绝对运动与局部观察之间不可兼得。

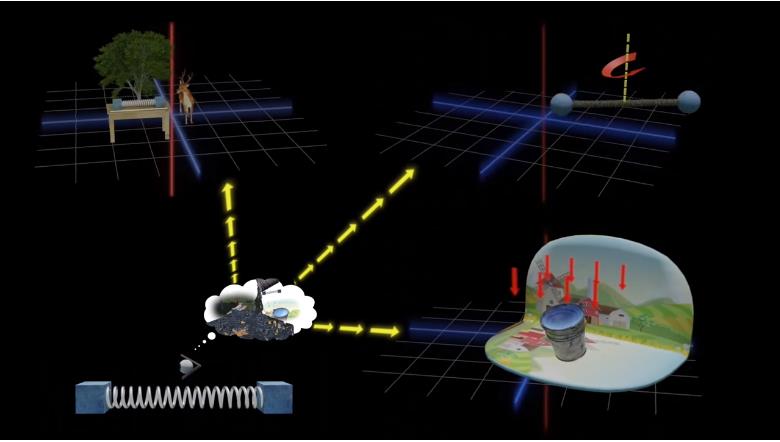
▲ 图2.7.2 先验知识实际上是扩大了实验空间范围

  对绝对运动不能要求观察者能够清晰判断，又要求不参考其它系统，两者中只能兼顾其一。 】】如果我们试图以记忆为代价来保持局部性，那么每个观察者的先验知识的不同，就会对运动状态判断有歧义，对于不同观察者的结论差异你也没有一个客观标准进行判断。】】另一方面，如果我们试图对运动状态能够进行客观判断，允许观察者可以使用记忆中的经验知识，那么判断结果是通过记忆来引用更大的系统提供的信息，所以就不是局部的。

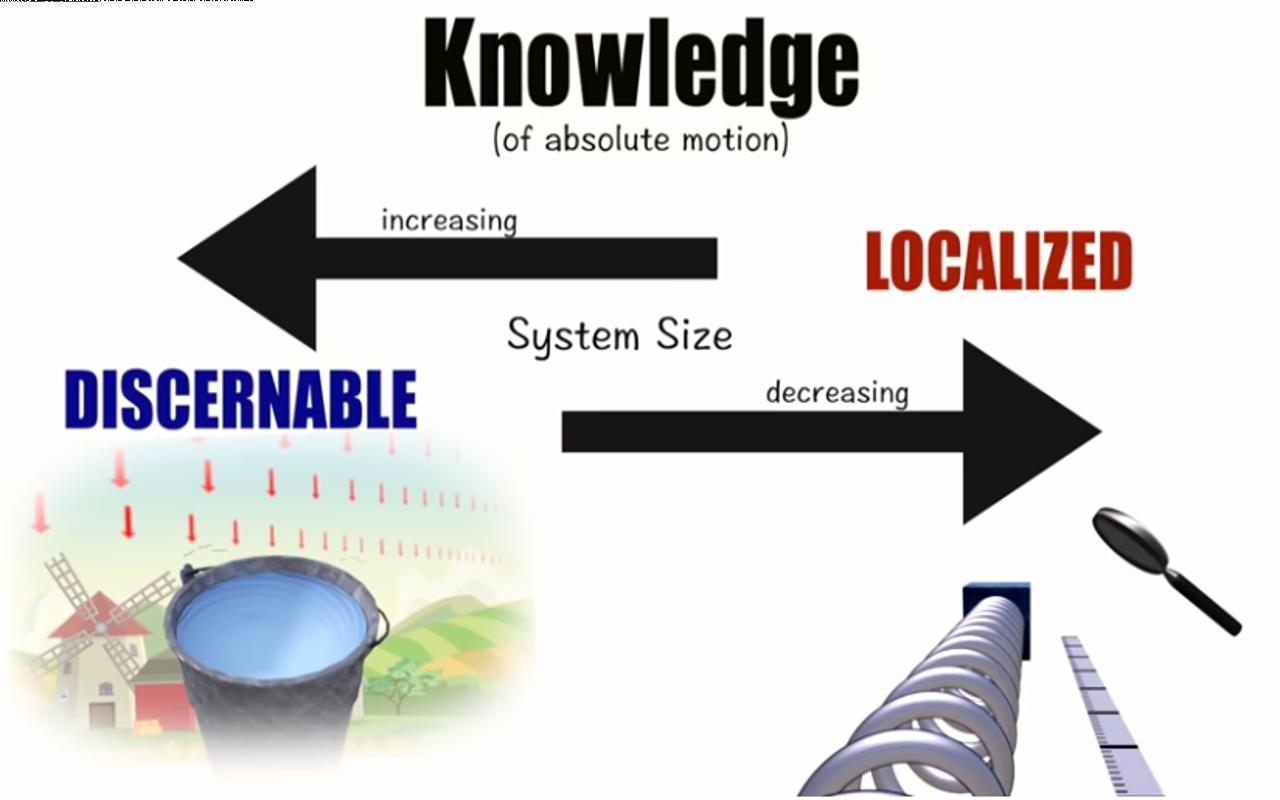
八、绝对运动两种观点

  通过以上讨论，关于是否存在绝对运动的辩论就产生了两种主要观点。 】】

  1、存在一种真实的和局部的绝对运动， 但有可能无法测量到这种绝对运动。 这相当于说存在一种绝对运动支配着我们的宇宙运作，但观察者有可能对其存在歧义。】】这个观点承认绝对运动或许是一种不可观察的现象，这个观点对于强调客观事实的物理学来说无法接受。

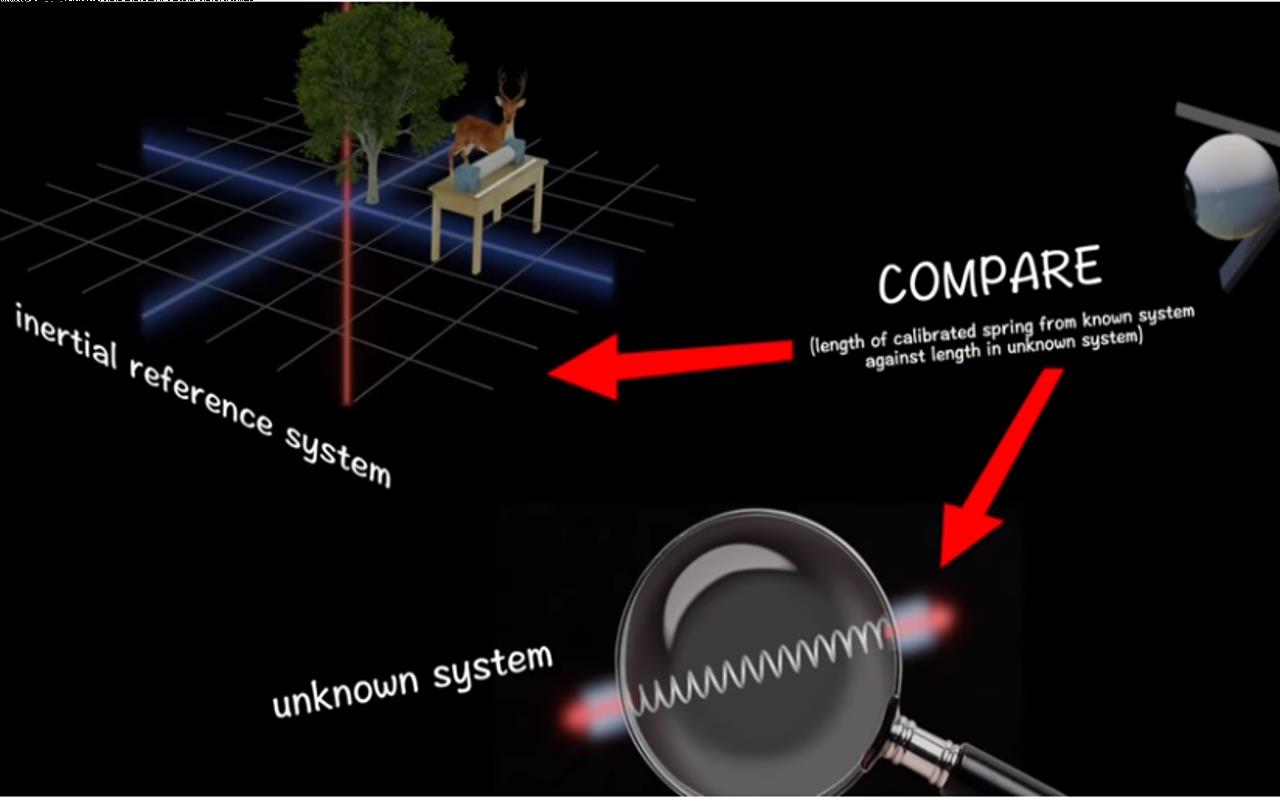
▲ 图2.7.3 观点1：存在绝对运动，并可以在局部验证

  2、不存在绝对运动，绝对运动实际上是整个宇宙相互联系系统中局部呈现出的特性，相关纠缠的系统组成部分不能从根本上相互隔离。 】】这个观点认为运动在某种程度上必须是相对的。】】那么这些答案中的哪一个是正确的呢？ 除了数学描述之外，绝对运动是否具有实际意义？ 或者它只是一个没有明确定义的概念？ 】】和绝对空间或绝对时间这样传统观念以外，对于绝对运动的观念也许要从根本上进行重新审视。对于这个观点，你有什么想法呢？

▲ 图2.8.2 关于牛顿的绝对时空观的争论

---

■ 相关文献链接:

• Newton vs. Mach: The Bucket Experiment

● 相关图表链接:

• 图2.1.1 艾萨克·牛顿与恩斯特·马赫
• 图2.1.2 水桶实验
• 图2.2.1 牛顿理论的三个绝对量
• 图2.2.2 通过一些相互依存的概念来发展我们的思想
• 图2.2.3 牛顿绝对物理量中的前两个崩塌了
• 图2.2.4 物理阵营分成两个学派
• 图2.3.1 牛顿的水桶实验
• 图2.3.2 与水桶一同旋转的观察者看到水桶和水也是静止的
• 图2.3.3 相对静置水桶旋转的观察者看到的水平面是平的
• 图2.3.4 水桶中的水面代表这绝对静止与绝对旋转
• 图2.3.5 马赫与牛顿的观点究竟谁是正确的呢？
• 图2.4.1 旋转水面切面是一条抛物线
• 图2.4.2 在无重力情况下，旋转的水桶将不会存在水面
• 图2.4.3 无重力下只有两种情况发生
• 图2.4.4 关于水桶思想实验，马赫胜出
• 图2.5.1 旋转小球实验
• 图2.5.2 通过测量连接弹簧的拉伸确定是否具有绝对旋转
• 图2.5.3 旋转小球实验满足绝对运动的假设
• 图2.6.1 上面两个状态表明运动和静止两个状态
• 图2.6.2 如何确定弹簧长度是最短的可能长度呢？
• 图2.6.3 在外部惯性系中获得弹簧最短长度
• 图2.6.4 旋转弹簧小球实验需要从惯性系中获得弹簧最短信息
• 图2.7.1 牛顿理论中关于实验观察者的假设推论
• 图2.7.2 先验知识实际上是扩大了实验空间范围
• 图2.7.3 存在绝对运动，并可以在局部验证
• 图2.8.2 关于牛顿的绝对时空观的争论