因果诊断原理

Posted 2023-01-24 tostq

因果分析在近十来年逐渐倍受关注，其提供了解释因子间因果性的定量分析工具，广泛用于数据分析领域，同时也就用决策分析、作用预估等反事实因果推理中。本文首先对比了因果性和相关性的关系，之后确定因果关系的基本方法，最后介绍了当下流行的基于模型的因果分析方法。

1. 什么是因果性和相关性

 首先相关性是很好理解的，代表两个随机变量之间可量化的相互关系，常用的反映相关系数的指标有协方差、相关系数等。相关性纯粹是指数据间的相互关系，这个关系是量的比例变动关系，其方向是对称双向的，比如A和B有相关性，即：

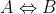
假设A=α*B，α是B对A的线性相关因子，代表了B增加1个单位，同时A会增加α单位，反过来说是正确的，A增加α单位，B会增加1个单位。

然而因果性是有方向，比如A是引起B的因，即：

因果性是单向的，只存在A对于B的因果影响，其代表了作用A会对B的影响，称之为Treatment Effect，这时读者可能会疑问，这里A对B的因果影响同上面算相关性时，描述的A增加α单位，会导致B增加1个单位有什么区别？除了描述问题名称不一样，这里的因果影响就不是相关性么？

确实是如此，如果是我们先前例子中，A和B完全是由单向箭头完全描述的情况，A对B的因果影响量完全可以用A对B的相关性来描述，但是在真实世界，这样的一对随机变量完全是不存在的，更为通用的形式是这样的：

 图中描述的是T对Y的因果影响图

• T表示treatment
• Y表示结果
• X表示对于T及Y都有影响的外在因子
• W表示仅对Y有影响的其他因子
• ε表示影响的误差因子

从上面更为通用因果描述中，T和Y的直接相关性没有办法来衡量T对Y的因果影响，因此存在X及W的混杂因子，所谓混杂因子会偏移T和Y数据上相关性计算，比如如下的例子。

另一方面，混杂因子的引入也会导致完全无因果性的变量出现强相关性。

所以因果方向性的引入完全是必要的，但这个方向是很难是数据中得出，而是从物理世界中获取先验知识来刻画的。然而部分统计学者认为因果性完全由人为设定，而不是从数据中获取，失去了数据统计的客观性，但图灵奖得主Judea Pearl反对这种观点，其认为通过先验知识来刻画因子间的因果图或者因果路径，就如同贝叶斯里的先验一样，这种引入是完全有必要的，而纯粹通过数据间的相关性是完全不能反映因果性的。

Judea Pearl给出了计算因果影响的一般性方法：

• 首先是建立问题的假设（比如吸烟是否会导致肺癌）、围绕问题的相关变量以及变量间关系的知识经验。
• 刻画所有变量的因果模型（因果图、结构方程等），由因果路径来表示变量间的因果或者导赂关系。
• 确定干预因子（称为treatment或者do(T)）以及影响的结果因子Y，即E(Y|do(T))
• 利用因果模型来计算E(Y|do(T))，包含了识别去除混杂因子影响

这里包含了几个概念：

• 干预do(X)是指作用X，这里用do是表示并不是结果而是干预的动作，包含了反事实的逻辑
• 反事实：对一直吸烟的人，我们想知道其不吸烟情况下身体会怎样，这种在现实中完全不可能实现的假设，就是一类反事实推理，其中假设不吸烟可以用do(不吸烟）表示，对于吸烟的人永远不可能存在不吸烟的情况，所以do(不吸烟）表示的是假设的干预动作，而不是结果的数据。
• 平均干预影响Average Treatment Effect：或者可以视为因果性的描述，比如是否吸烟对患癌概率的影响可以表示为如下，即吸烟时患癌期望减去不吸烟患癌的期望。

• CATE：针对于某一个个体类X的平干预影响，即：

上面的几个概念中，因果模型计算的重点在于计算 E(Y|do(T))，即去除do算子。下一节将介绍Judea Pearl的几个基本消除do算子的方法。

2. 确定因果性的基本方法

 在上一节中，我们提到如果T对Y的影响完全可以由单向箭头描述的情况下，T对Y的因果性可以由数据相关性描述，即

这种情况下，do算子被简单消除了。另一方面是通过分层统计的方式消除do算子，对于同一层中除了干预因子外，其他混杂因子都是一致的，或者通过随机测试实验也可以实现do算子。但前者需要大量的统计数据，后者不一定可实验（比如不能强迫吸烟）。

因为信息在因果图中流动，由于信息传递是双向的（相关性），有些是因果方向传递，有些在非因果方向传递。而求因果效应必须要去除所有的非因果路径，这个实际上就是去混杂因子的过程，也是do算子需要做的事。

常见阻断信息流的方法：

• A→B→C，控制B可以避免信息流动，即B一旦观察到，A的信息就无法作用到C
• A←B→C，控制B可以避免信息流动
• A→B←C，不控制B可以避免信息流动，
• 控制一个变量的后代节点就如同”部分地”控制变量本身：
  • 控制A→B→C中的中介物B的某个后代节点如同”部分地”关闭了信息管道
  • 控制A→B←C中的对撞物B的某个后代节点如同”部分地”打开了信息管道

此外Judea Pearl还给出了另外几个去除do算子的范式：

后门路径backdoor：

• 寻找后门路径：指向T且存在T同Y之前的信息流通，即图中的X->T
• 当完全阻断全部的后门路径后，P(Y|do(T))=P(Y|T)，上式中的X表示要控制全部后门变量。后门路径公式实际表示，通过估计每个去混因子在不同水平的效应，并据此测算出干预的平均因果效应，计算各层的因果效应的加权平均值P(z)，即对每个层因果效应P(Y|T=t,X=x)都按其在总体中的分布频率P(X)进行加权，后门路径的原理类似于分层统计。

前门路径frontdoor：

 

• 寻找前门路径：指T指向Y的因果路径中存在中介因子M，即T→M→Y
• 前门公式从直观上分成两个部分：
  • 前一部分平均T->M的因果效应，此时只有唯一的信息流通路径，即：
  • 
  • 后一项表示M->Y的因果效应，可通过后门效应控制去除do(M)算子，即：
  • 

更为通用的do算子：

• 规则1：如果变量W同Y无关（可能在控制Z时）则P(Y|do(X),Z,W)=P(Y|do(x),Z)
• 规则2：如果Z阻断X到Y的全部后门路径，则P(Y|do(X),Z)=P(Y|X,Z)
• 规则3：如果X到Y之间没有任何的因果路径（即不存在只包含前向箭头的从X到Y的路径），则P(Y|do(X))=P(Y)
• 前门公式的推导：
• 

通过上述范式可以根据因果图来消除TE（treatment effect）计算式子中的do算子，Microsoft提供了开源python库dowhy实现上述前门、后门、do算子的逻辑，但是上述我们讨论计算TE本质上是基于概率图推理的，对于高维的特征以及针对于个体特定因果影响（即CTE）在计算上非常困难。在下一节，我们将讨论基于机器学习的因果推理即CML（causal machine learning）。

3. 基于机器学习的因果推理CML

 基于机器学习的因果推理模型最为主要的范式是DML，即Double Machine Learning，其基本思想是通过残差计算来消除do算子。

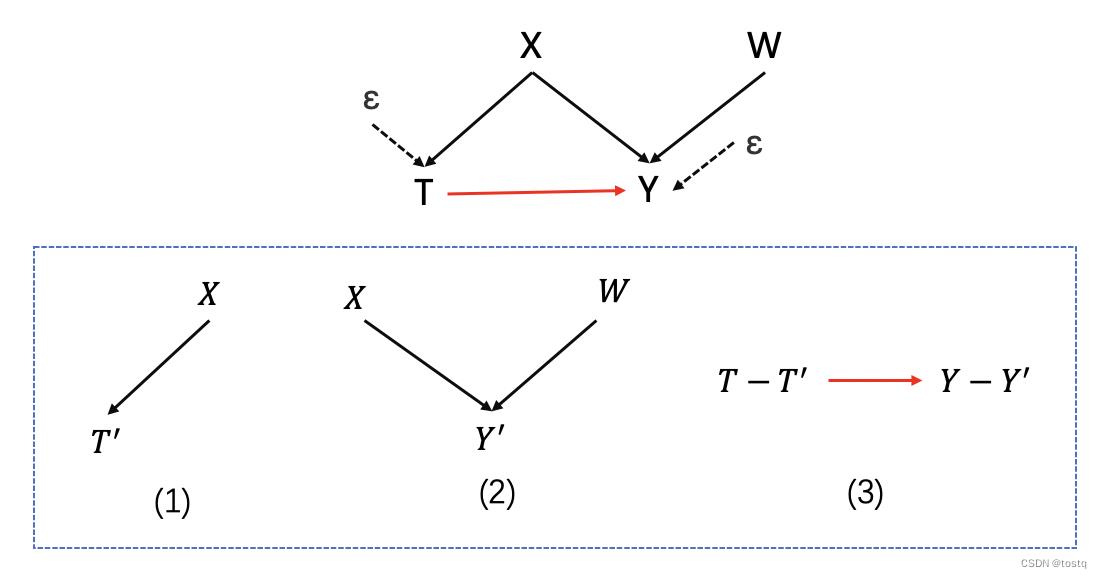
 如上图通过残差形式将原因果图拆分为三个部分，具体方式如下：

• 建立模型T'=M(X)
• 建立模型Y'=M(X,W)
• 建立残差模型T-T'=M(Y-Y')

训练一般采用Cross-fitting的方式，即把样本分成两部分，先用样本1分别预估T'和Y'两个模型，再用样本2估计残差模型，最后再交换估计，然后取两轮预估参数平均得到最终的模型。

通过机器学习模型的方式，我们摆脱了上一节的概率图模型，可以用更为复杂的机器学习模型来估计因果影响面。具体我们可以参考Microsoft的开源工具econml，其提供了DML的实现框架。