pytorch 笔记：torch.nn.init
Posted UQI-LIUWJ
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了pytorch 笔记：torch.nn.init相关的知识，希望对你有一定的参考价值。
这个模块中的所有函数都是用来初始化神经网络参数的，所以它们都在torch.no_grad()模式下运行，不会被autograd所考虑。
1 计算gain value
1.1 介绍
这个在后面的一些nn.init初始化中会用到
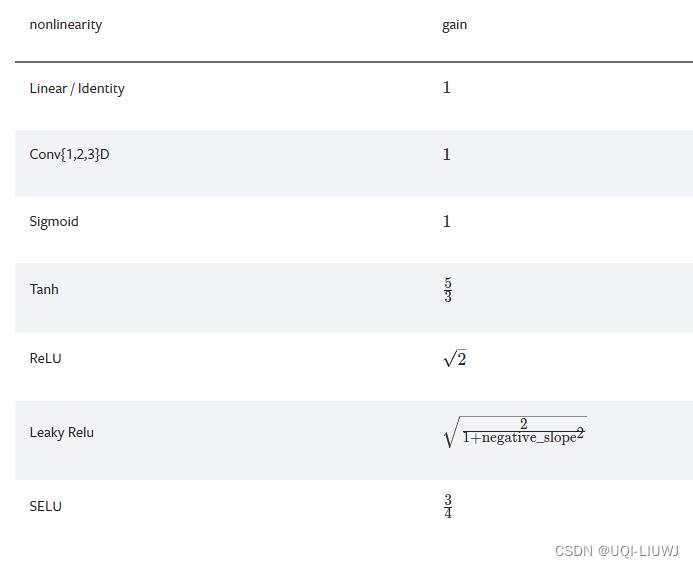
1.2 用法
torch.nn.init.calculate_gain(nonlinearity, param=None)import torch
torch.nn.init.calculate_gain('sigmoid')
#1
torch.nn.init.calculate_gain('tanh')
#1.6666666666666667
torch.nn.init.calculate_gain('leaky_relu',0.1)
#1.4071950894605838
torch.nn.init.calculate_gain('conv3d')
#12 初始化汇总
2.1 均匀分布
以均匀分布U(a,b)填充tensor
torch.nn.init.uniform_(tensor, a=0.0, b=1.0)a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.uniform_(a,3,5)
a
'''
tensor([[3.2886, 3.5971, 3.3080, 4.5271, 4.3113],
[4.3634, 4.1311, 3.4466, 3.3745, 3.9957],
[4.7776, 4.4654, 4.7397, 3.5465, 4.5716]])
'''2.2 正态分布
以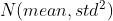
初始化tensor
torch.nn.init.normal_(tensor, mean=0.0, std=1.0)a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.normal_(a,0,5)
a
'''
tensor([[-9.6473, -0.8678, -7.0850, -1.3568, -6.1306],
[-5.5031, -1.6662, 9.8144, -6.5255, -6.2179],
[-0.6455, -1.7757, 7.7232, -1.2374, -1.2551]])
'''2.3 定值
以定值初始化
torch.nn.init.constant_(tensor, val)a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.constant_(a,5)
a
'''
tensor([[5., 5., 5., 5., 5.],
[5., 5., 5., 5., 5.],
[5., 5., 5., 5., 5.]])
'''2.4 填充1
用定值1初始化
torch.nn.init.ones_(tensor)a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.ones_(a)
a
'''
tensor([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
'''2.5 填充0
用定值0初始化
torch.nn.init.zeros_(tensor)
a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.zeros_(a)
a
'''
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
'''
2.6 使用单位矩阵进行初始化
torch.nn.init.eye_(tensor)
a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.eye_(a)
a
'''
tensor([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.]])
'''
2.7 Xavier 均匀初始化
torch.nn.init.xavier_uniform_(tensor, gain=1.0)根据《Understanding the difficulty of training deep feedforward neural networks》，使用U(-a,a)进行初始化，其中
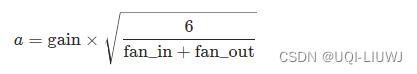
这里的gain就是 torch.nn.init.calculate_gain输出的内容
a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.xavier_uniform_(a,
gain=torch.nn.init.calculate_gain('relu'))
a
'''
tensor([[-1.0399, -0.5018, 0.2838, 1.1071, 0.0897],
[-0.9356, 0.9661, -0.6718, -1.0132, 0.9140],
[ 0.9704, 0.8222, 0.2229, -1.1519, 0.4566]])
'''2.8 Xavier 正态初始化
torch.nn.init.xavier_normal_(tensor, gain=1.0)根据《Understanding the difficulty of training deep feedforward neural networks》，使用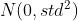
进行初始化，其中
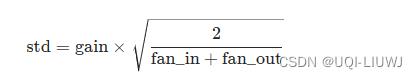
这里的gain就是 torch.nn.init.calculate_gain输出的内容
a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.xavier_uniform_(a,
gain=torch.nn.init.calculate_gain('relu'))
a
'''
tensor([[-1.0399, -0.5018, 0.2838, 1.1071, 0.0897],
[-0.9356, 0.9661, -0.6718, -1.0132, 0.9140],
[ 0.9704, 0.8222, 0.2229, -1.1519, 0.4566]])
'''2.9 Kaiming 均匀
根据《Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification》，使用U(-bound,bound)
其中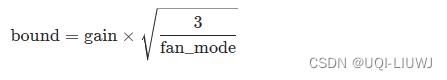
torch.nn.init.kaiming_uniform_(tensor,
a=0,
mode='fan_in',
nonlinearity='leaky_relu')只有当nonlinearity为leaky_relu的时候，a有意义（表示负的那一部分的斜率）
a=torch.Tensor(3,5)
a
'''
tensor([[9.2755e-39, 8.9082e-39, 9.9184e-39, 8.4490e-39, 9.6429e-39],
[1.0653e-38, 1.0469e-38, 4.2246e-39, 1.0378e-38, 9.6429e-39],
[9.2755e-39, 9.7346e-39, 1.0745e-38, 1.0102e-38, 9.9184e-39]])
'''
torch.nn.init.kaiming_uniform_(a,
mode='fan_out',
nonlinearity='relu')
a
'''
tensor([[ 0.7745, -1.0520, -0.3770, 0.7101, 0.9383],
[ 1.0138, 0.6069, -0.5126, -0.3454, 1.2242],
[ 0.3531, 0.2758, 0.3740, -0.8026, 1.1270]])
'''2.10 kaiming正态
根据《Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification》，使用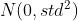进行初始化，其中
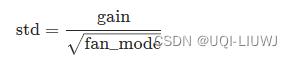
a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.kaiming_normal_(a,
mode='fan_out',
nonlinearity='relu')
a
'''
tensor([[ 1.1192, -0.6108, -1.2601, 0.4863, 0.4850],
[ 0.8790, -0.1947, 0.3900, -0.1621, 0.0261],
[-0.5602, -2.0269, 0.1730, -1.4321, 0.1675]])
'''2.11 截断正态分布
torch.nn.init.trunc_normal_(tensor, mean=0.0, std=1.0, a=- 2.0, b=2.0)如果初始化的某一些元素不在[a,b]之间，那么就重新随机选取这个值
a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.trunc_normal_(a,
a=-0.2,
b=0.8)
a
'''
tensor([[ 0.4685, 0.7272, 0.1331, -0.0746, 0.4909],
[-0.1088, 0.4126, 0.4549, 0.0990, 0.3314],
[ 0.4176, 0.0785, 0.3213, 0.5305, 0.5663]])
'''2.12 初始化稀疏矩阵
torch.nn.init.sparse_(tensor, sparsity, std=0.01)sparsity表示每一列多少比例的元素是0
std表示每一列以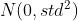的方式选择非负值
a=torch.Tensor(3,5)
a
'''
tensor([[9.8265e-39, 9.4592e-39, 1.0561e-38, 7.3470e-39, 1.0653e-38],
[1.0194e-38, 1.0929e-38, 1.0102e-38, 1.0561e-38, 1.0561e-38],
[1.0561e-38, 1.0745e-38, 1.0561e-38, 8.7245e-39, 9.6429e-39]])
'''
torch.nn.init.sparse_(a,sparsity=0.3)
a
'''
tensor([[ 0.0000, 0.0074, -0.0044, -0.0046, 0.0000],
[-0.0091, 0.0000, -0.0111, -0.0024, 0.0047],
[-0.0004, 0.0037, 0.0000, 0.0000, 0.0007]])
'''3 fan_in 与 fan_out
下面是kaiming 初始化中对fan_mode的说法
- "fan_in"可以保留前向计算中权重方差的大小。
- Linear的输入维度
- Conv2d：
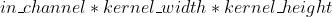
- "fan_out"将保留后向传播的方差大小。
- Linear的输出维度
- Conv2d:
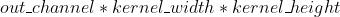
3.1 Pytorch的计算方式
Linear：
net=torch.nn.Linear(3,5)
net
#Linear(in_features=3, out_features=5, bias=True)
torch.nn.init._calculate_fan_in_and_fan_out(net.weight)
#(3,5)
torch.nn.init._calculate_correct_fan(net.weight,
mode='fan_in')
#3
torch.nn.init._calculate_correct_fan(net.weight,
mode='fan_out')
#5Conv2d
net=torch.nn.Conv2d(kernel_size=(3,5),
in_channels=2,
out_channels=10)
net
#Conv2d(2, 10, kernel_size=(3, 5), stride=(1, 1))
torch.nn.init._calculate_fan_in_and_fan_out(net.weight)
#(30,150)
torch.nn.init._calculate_correct_fan(net.weight,
mode='fan_in')
#30 （2*3*5）
torch.nn.init._calculate_correct_fan(net.weight,
mode='fan_out')
#150 （10*3*5）以上是关于pytorch 笔记：torch.nn.init的主要内容，如果未能解决你的问题，请参考以下文章