Path&PathMeasure完全解析
Posted 花花young
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Path&PathMeasure完全解析相关的知识,希望对你有一定的参考价值。
前言
Path扮演着路径的角色,在绘制View起着非常重要的位置,而PathMeasure是对Path进行测量,通过使用PathMeasure可以更加方便的使用Path工具。网上都好多关于这方面的文章,在这里只是做个笔录,不好不要见怪。嘿嘿
Part 1、谈谈Path的使用
首先先分析方法
public class Path
/**
* 空构造方法
*/
public Path()
mNativePath = init1();
/**
* 重置Path
*/
public void reset()
isSimplePath = true;
mLastDirection = null;
if (rects != null) rects.setEmpty();
// We promised not to change this, so preserve it around the native
// call, which does now reset fill type.
final FillType fillType = getFillType();
native_reset(mNativePath);
setFillType(fillType);
/**
* 和reset一样,只不过这个会将FillType也清楚掉,但reset不会
*/
public void rewind()
isSimplePath = true;
mLastDirection = null;
if (rects != null) rects.setEmpty();
native_rewind(mNativePath);
/**
* Path和Path之间的运算方法
*/
public boolean op(Path path, Op op)
return op(this, path, op);
/**
* 得到填充的类型
*/
public FillType getFillType()
return sFillTypeArray[native_getFillType(mNativePath)];
/**
* 设置Path的填充类型
*/
public void setFillType(FillType ft)
native_setFillType(mNativePath, ft.nativeInt);
/**
* 判断是否反向填充
*/
public boolean isInverseFillType()
final int ft = native_getFillType(mNativePath);
return (ft & FillType.INVERSE_WINDING.nativeInt) != 0;
/**
* 计算Path所占用的空间以及位置,将信息存入bounds中,exact:是否精确测量
*/
@SuppressWarnings("UnusedDeclaration")
public void computeBounds(RectF bounds, boolean exact)
native_computeBounds(mNativePath, bounds);
/**
* 自动改变,取反
*/
public void toggleInverseFillType()
int ft = native_getFillType(mNativePath);
ft ^= FillType.INVERSE_WINDING.nativeInt;
native_setFillType(mNativePath, ft);
/**
* Path是否为空
*/
public boolean isEmpty()
return native_isEmpty(mNativePath);
/**
* 将画笔移动的坐标位置
*/
public void moveTo(float x, float y)
native_moveTo(mNativePath, x, y);
/**
* 和上面一样,只不过上面是绝对位置,这个是相对位置(相对于上一个点)
*/
public void rMoveTo(float dx, float dy)
native_rMoveTo(mNativePath, dx, dy);
/**
* 在lineTo之前要先moveTo否则则将默认为从原点开始划线
*/
public void lineTo(float x, float y)
isSimplePath = false;
native_lineTo(mNativePath, x, y);
/**
* 于lineTo相对,这个是相对位置
*/
public void rLineTo(float dx, float dy)
isSimplePath = false;
native_rLineTo(mNativePath, dx, dy);
/**
* 二阶贝塞尔曲线
*/
public void quadTo(float x1, float y1, float x2, float y2)
isSimplePath = false;
native_quadTo(mNativePath, x1, y1, x2, y2);
/**
*
*/
public void rQuadTo(float dx1, float dy1, float dx2, float dy2)
isSimplePath = false;
native_rQuadTo(mNativePath, dx1, dy1, dx2, dy2);
/**
* 三阶贝塞尔曲线
*/
public void cubicTo(float x1, float y1, float x2, float y2,
float x3, float y3)
isSimplePath = false;
native_cubicTo(mNativePath, x1, y1, x2, y2, x3, y3);
/**
*
*/
public void rCubicTo(float x1, float y1, float x2, float y2,
float x3, float y3)
isSimplePath = false;
native_rCubicTo(mNativePath, x1, y1, x2, y2, x3, y3);
/**
* 画弧线
*/
public void arcTo(RectF oval, float startAngle, float sweepAngle,
boolean forceMoveTo)
arcTo(oval.left, oval.top, oval.right, oval.bottom, startAngle, sweepAngle, forceMoveTo);
/**
* 当调用close则将结束点和起始点连线
*/
public void close()
isSimplePath = false;
native_close(mNativePath);
/**
* 绘制的方向
*/
public enum Direction
CW (0), // 顺时针方向
CCW (1); //逆时针
Direction(int ni)
nativeInt = ni;
final int nativeInt;
/**
* 提供了大量的add图形的方法(将更多的图片添加到Path路径便于设置方向、填充方式)
*/
public void addXXX(XXX)
/**
* 将Path进行偏移,偏移之后的结果存入dst中
*/
public void offset(float dx, float dy, @Nullable Path dst)
if (dst != null)
dst.set(this);
else
dst = this;
dst.offset(dx, dy);
/**
* 将Path进行偏移,偏移之后的结果写入path中
*/
public void offset(float dx, float dy)
if (isSimplePath && rects == null)
// nothing to offset
return;
if (isSimplePath && dx == Math.rint(dx) && dy == Math.rint(dy))
rects.translate((int) dx, (int) dy);
else
isSimplePath = false;
native_offset(mNativePath, dx, dy);
(1)Path运算:
/**
* Path和Path之间的运算
*/
public enum Op
/**
* path1中减去Path2剩下的部分
*/
DIFFERENCE,
/**
* path1和path2相交的部分
*/
INTERSECT,
/**
* 包含path1和path2部分
*/
UNION,
/**
*包含path和path2但不包含相交的部分
*/
XOR,
/**
* Path2减去Path1剩下的部分
*/
REVERSE_DIFFERENCE

根据Path的运算我们可以实现一个八卦图的效果
效果~

实现起来非常简单,只需要利用上面的运算规则即可,这里就不多说,直接上代码。
canvas.translate(getWidth() / 2, getHeight() / 2);
canvas.save();
for (int i = 0; i < 2; i++)
path1.addCircle(0, 0, 200, Path.Direction.CW);
path2.addRect(-200, -200, 0, 200, Path.Direction.CW);
path1.op(path2, Path.Op.INTERSECT);//去相交的区域
path2.reset();
path2.addCircle(0, -100, 100, Path.Direction.CCW);
path1.op(path2, Path.Op.UNION);//去全部的区域
path2.reset();
path2.addCircle(0, 100, 100, Path.Direction.CW);
path1.op(path2, Path.Op.DIFFERENCE);//取Path1减去path2的区域
canvas.drawPath(path1, paint);
canvas.rotate(180, 0, 0);
canvas.restore();
paint.setShader(new RadialGradient(0, -100, 25, Color.WHITE, Color.BLACK, Shader.TileMode.MIRROR));
canvas.drawCircle(0, -100, 25, paint);
paint.setShader(new RadialGradient(0, 100, 25, Color.BLACK, Color.WHITE, Shader.TileMode.MIRROR));
canvas.drawCircle(0, 100, 25, paint);(2)Path的填充:
/**
* Enum for the ways a path may be filled.
*/
public enum FillType
// these must match the values in SkPath.h
/**
* 非零环绕数规则
*/
WINDING (0),
/**
*奇偶规则
*/
EVEN_ODD (1),
/**
* 反非零环绕数规则
*/
INVERSE_WINDING (2),
/**
* 反奇偶规则
*/
INVERSE_EVEN_ODD(3);
FillType(int ni)
nativeInt = ni;
final int nativeInt;
网址:http://blog.csdn.net/u013831257/article/details/51477575
奇偶规则:从任意位置p作一条射线, 若与该射线相交的图形边的数目为奇数,则p是图形内部点,否则是外部点。
非零环绕数规则:首先使图形的边变为矢量。将环绕数初始化为零。再从任意位置p作一条射线。当从p点沿射线方向移动时,对在每个方向上穿过射线的边计数,每当图形的边从右到左穿过射线时,环绕数加1,从左到右时,环绕数减1。处理完图形的所有相关边之后,若环绕数为非零,则p为内部点,否则,p是外部点。
接下来我们先了解一下两种判断方法是如何工作的。
奇偶规则(Even-Odd Rule)
这一个比较简单,也容易理解,直接用一个简单示例来说明。
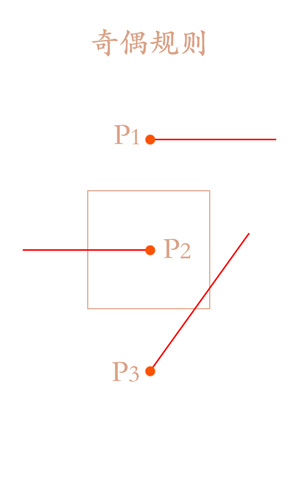
在上图中有一个四边形,我们选取了三个点来判断这些点是否在图形内部。
P1: 从P1发出一条射线,发现图形与该射线相交边数为0,偶数,故P1点在图形外部。
P2: 从P2发出一条射线,发现图形与该射线相交边数为1,奇数,故P2点在图形内部。
P3: 从P3发出一条射线,发现图形与该射线相交边数为2,偶数,故P3点在图形外部。
非零环绕数规则(Non-Zero Winding Number Rule)
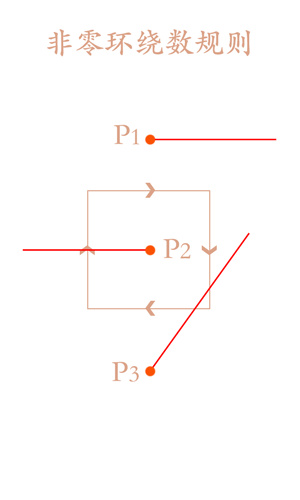
P1: 从P1点发出一条射线,沿射线防线移动,并没有与边相交点部分,环绕数为0,故P1在图形外边。
P2: 从P2点发出一条射线,沿射线方向移动,与图形点左侧边相交,该边从左到右穿过穿过射线,环绕数-1,最终环绕数为-1,故P2在图形内部。
P3: 从P3点发出一条射线,沿射线方向移动,在第一个交点处,底边从右到左穿过射线,环绕数+1,在第二个交点处,右侧边从左到右穿过射线,环绕数-1,最终环绕数为0,故P3在图形外部。
通常,这两种方法的判断结果是相同的,但也存在两种方法判断结果不同的情况,如下面这种情况:
注意图形线段的方向,就不详细解释了,用上面的方法进行判断即可。
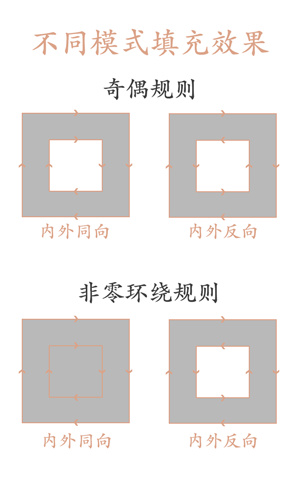
通过上面的介绍进行验证
path.op(path1, ops[i - 1]);
canvas.drawPath(path, paint); 
对于FillType=EVENT_ODD的时候,CCW和CW效果是一样的,但对于WINDING就需要考虑的绘制的方向
leftCenterX = startX + smallWidth * (i % 2);
leftCenterY = startY + smallHeight * (i / 2);
path.setFillType(Path.FillType.WINDING);
path.addCircle(centerX, centerY, raduis, Path.Direction.CCW);
path.addCircle(centerX, centerY, centerRadios - 50, Path.Direction.CCW);
canvas.drawPath(path, paint);根据上面的规则来做一个环嵌套环的效果

Part 2、PathMeasure的使用
首先先分析方法
public class PathMeasure
private Path mPath;
/**
* 创建一个空的PathMeasure
*/
public PathMeasure()
mPath = null;
native_instance = native_create(0, false);
/**
* 用这个构造函数可创建一个空的PathMeasure,但是使用之前需要先调用setPath方法来与Path进行关联。
* 被关联的Path必须是已经创建的好的,如果关联之后Path的内容进行了更改则需要使用setPath方法重新进行关联
*/
public PathMeasure(Path path, boolean forceClosed)
// The native implementation does not copy the path, prevent it from being GC'd
mPath = path;
native_instance = native_create(path != null ? path.readOnlyNI() : 0,
forceClosed);
/**
* 用这个构造函数是创建一个PathMeasure并关联一个Path,其实和创建一个空的PathMeasure后调用setPath进行关联效果是一样的
* 同样被关联的Path也必须已经是创建好的,如果关联的Path内容进行了更改,则需要是用setPath方法重新关联。
* 第二个参数是用来确保Path闭合,如果设置为true,则不论之前是否闭合,都会自动闭合该Path(如果Path可以闭合的话)
* 这里需要注意:
* 1、不论forceClosed设置为何种状态都不会影响原有的状态,即Path与PathMeasure关联之后,之前的Path不会有任何的改变
* 2、forceClosed的设置状态可能会影响测量结果,如果Path未闭合但在与PathMeasure关联的时候设置了true,则测量的结果
* 可能会比Path实际的长度稍长一点,获取到是该Path闭合的状态
*/
public void setPath(Path path, boolean forceClosed)
mPath = path;
native_setPath(native_instance,
path != null ? path.readOnlyNI() : 0,
forceClosed);
/**
* 获取Path的总长度
*/
public float getLength()
return native_getLength(native_instance);
/**
* 用于得到路径上某一长度位置以及该位置的正切值
* 返回值:判断是否获取成功 true表示成功,数据会存入pos和tan中
* 参数
* distance : 距离Path起点的长度 取值范围0<=distance<=getLength
* pos : 该点的坐标值
* tan : 该点的正切值
*/
public boolean getPosTan(float distance, float pos[], float tan[])
if (pos != null && pos.length < 2 ||
tan != null && tan.length < 2)
throw new ArrayIndexOutOfBoundsException();
return native_getPosTan(native_instance, distance, pos, tan);
public static final int POSITION_MATRIX_FLAG = 0x01; // must match flags in SkPathMeasure.h
public static final int TANGENT_MATRIX_FLAG = 0x02; // must match flags in SkPathMeasure.h
/**
* 用于得到路径上某一长度的位置以及该位置的正切值矩阵
* 返回值:判断获取是否成功
* 参数
* 1、distance :距离起点的长度
* 2、matrix : 根据flags封装好的matrix,会根据flags的位置而存入不同的内容
* 3、flags : 规定哪些内容会存入到matrix中,可选择POSITION_MATRIX_FLAG(位置) ANGENT_MATRIX_FLAG(正切)
*/
public boolean getMatrix(float distance, Matrix matrix, int flags)
return native_getMatrix(native_instance, distance, matrix.native_instance, flags);
/**
* 获取Path的一个片段
* 返回值:判断截取是否成功,true表示截取成功,结果存入dst中,false表示截取失败,不会存在dst中
* 参数
* startD:开始截取位置距离Path起点的长度,取值范围 0 <=startD<stopD<=path总长度
stopD:结束截取位置距离Path起点的长度,取值范围 0<=startD<stopD<=path总长度
* dst : 截取的Path将会添加到dst中,注意是添加不是替换
* startWithMove: 起始点是否使用moveTo,用于保证截取的Path第一个点位置不变
* true:保证截取片段不会发生变形 false : 保证截取片段的Path连续性
* 注意:
* 1、如果startD、stopD的数值不在取值范围【0,getLength】内,或者startD==stopD则返回false,不会改变dst的内容
* 2、如果在android4.4或者之前的版本,在默认开启硬件加速的情况下,更改了dst的内容后可能会出现问题,请在关闭
* 硬件加速或者给dst添加一个单个操作,例如dst.rLineTo(0,0)
* 3、可以用一下的规则来判断startWithMoveTo的取值
*/
public boolean getSegment(float startD, float stopD, Path dst, boolean startWithMoveTo)
// Skia used to enforce this as part of it's API, but has since relaxed that restriction
// so to maintain consistency in our API we enforce the preconditions here.
float length = getLength();
if (startD < 0)
startD = 0;
if (stopD > length)
stopD = length;
if (startD >= stopD)
return false;
return native_getSegment(native_instance, startD, stopD, dst.mutateNI(), startWithMoveTo);
/**
* 用来判断Path是否闭合,但是如果你在关联Path的时候设置了forceClosed在true的话,这个方法的返回值则一定为true
*/
public boolean isClosed()
return native_isClosed(native_instance);
/**
* Path是可以由多条曲线构成的,但不论是getLength,getSegment或者是其它的方法,都只会在其中的第一条线段上运行,
* 而这个nextContour就是用于跳转到下一条曲线的方法,如果跳转成功则返回true,如果跳转失败则返回false
*/
public boolean nextContour()
return native_nextContour(native_instance);
理论都介绍完了,来实现一个如下效果
效果~

思路:不断的去对矩形进行截取片段在绘制
Path dst1 = new Path();
pathMeasure3.getSegment(changeD, pathMeasure3.getLength(), dst1, true);
canvas.drawPath(dst1, paint);
Path dst2 = new Path();
pathMeasure3.getSegment(0, 100 - pathMeasure3.getLength() + changeD, dst2, true);
canvas.drawPath(dst2, paint);效果~
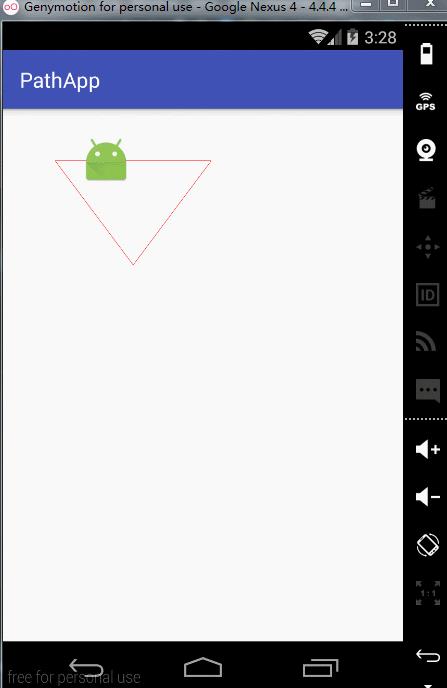
实现代码
PathMeasure pathMeasure = new PathMeasure(path, true);
float[] pos = new float[2];
float[] tan = new float[2];
pathMeasure.getPosTan(distance, pos, tan);
Bitmap bitmap = BitmapFactory.decodeResource(getResources(), R.mipmap.ic_launcher);
Matrix matrix = new Matrix();
//计算方位角
float degrees = (float) (Math.atan2(tan[1], tan[0]) * 180.0 / Math.PI);
matrix.postRotate(degrees, 50, 50);
matrix.postTranslate(pos[0] - 50, pos[1] - 50);
canvas.drawBitmap(bitmap, matrix, null);1、Math.atan2() : 与之比较的是Math.atan(),Math.atan的范围是-pi/2~pi/2之间,Math.atan2()是-pi~pi之间,得到的是弧度需要进一步进行转化为角度值

2、你也可以使用getMatrix方法来使用现成的矩阵,只不过这个矩阵是以左上角为原点
以上是关于Path&PathMeasure完全解析的主要内容,如果未能解决你的问题,请参考以下文章
Android UIPath 测量 PathMeasure ③ ( 使用 PathMeasure 绘制沿曲线运动的小球 )