数据结构与算法(Python)——常见数据结构Part2(栈和递归)

Posted 2022-11-28 The fool

写在前面

在上一节part1我们熟悉数组和链表，本节继续对其他常见数据结构进行总结。我们的目的是快速了解他们，对于它们涉及到的复杂的数据结构和算法，在这里并不全部展开，留在后期详述。

1. 栈

栈(stack)也是一种线性结构，与数组不同的是，栈限定了只能在线性表的一端，例如尾部进入插入或者删除操作(只允许头部操作类似)。

栈类似于把车开入了一个死胡同，只剩下一端，只能从这个入口进入或者出去，这个进入称之为入栈操作(push)，退出则称之为出栈操作(pop)。最后在这个死胡同里，车子只能从最后进入的那位开始依次往后倒车开出去，这就是连续出栈操作，直到栈为空。在出栈过程中，最先进入的最后出去，这称之为后进先出(Last In First Out,LIFO)。

在数据结构中，栈中一般存储同类型元素，当然也允许存储不同类型元素，例如动态语言中实现的栈。栈的操作如下图所示(图片来自tutorial point):

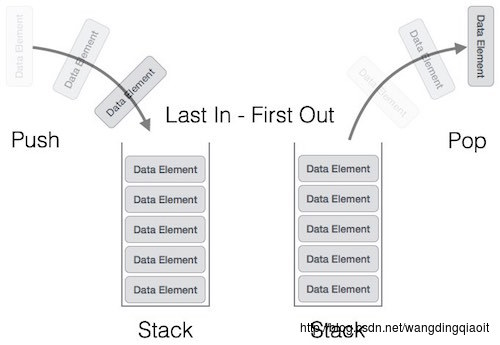
1.1 栈的实现

Python中没有显式提供栈结构，不过list结构可以当做栈来使用。
入栈和出栈操作实现为:

    stack = ['a']
    stack.append('b')   # 入栈操作
    stack.append('c')
    print(stack)   # ['a', 'b', 'c']
    content = stack.pop()  # 出栈操作
    print(content) # 'c'
    print(stack)   # ['a', 'b']

下面我们也对list进行一个封装，自己动手实现一个简单的栈。

class Stack(object):

    """
    栈
    """

    def __init__(self):
        self.data = []

    def __str__(self):
        output_str = "stack["
        for x in self.data:
            output_str += str(x)+","
        output_str += "]"
        return output_str

    def is_empty(self):
        return not self.data

    def push(self, element):
        self.data.append(element)

    def pop(self):
        return self.data.pop()

    def top(self):
        if self.data:
            return self.data[-1]
        else:
            return None

    def size(self):
        return len(self.data)

为上述类编写测试用例:

if __name__ == "__main__":
    stack = Stack()
    stack.push(5)
    stack.push(4)
    stack.push(3)
    print(stack)
    print("top:", stack.top())
    while not stack.is_empty():
        print("pop:", stack.top())
        stack.pop()
        print(stack)
    stack.push(6)
    print(stack)

程序输出:

stack[5,4,3,]
('top:', 3)
('pop:', 3)
stack[5,4,]
('pop:', 4)
stack[5,]
('pop:', 5)
stack[]
stack[6,]

1.2 栈的应用

栈结构的一个特点在于，先进来的元素后出栈，这样可以保持两个重要特性:

• 1)可以使用栈来对元素顺序进行逆转
• 2) 如果一个算法需要保存之前状态，在将来某个时间用上的话，可以借助栈来实现。

第一个特性能处理的典型问题例如逆序一个字符串，将字符串中元素压入栈，然后依次出栈则得到逆序字符串。例如判断是一个字符串是否回文（正着念和反着念是相同的字符串，例如”level” 、“aaabbaaa”、“上海自来水来自海上”），一种解决方法是将原始字符串依次入栈，然后依次出栈与原始字符对比，即可判定是否为回文字符串。

第二个特性尤其重要，典型问题例如括号匹配检查问题和迷宫问题。

1.2.1 括号匹配问题

给定一个包含”,[,(,,],)”括号的字符串，检查括号是否配对，例如”[([])]”是配对的括号，而”]([)”则不是配对的括号字符。这个题目中一个明显的感觉是: 要判断括号匹配或者不匹配，我们最好是在看到了右侧括号后，回过头来检查是否有对应的左侧括号，这种回过头来查看数据的操作暗示了要使用栈这种记忆先前状态的特性，因此可以通过栈来实现。这里我们给出一个解决方法：

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        if not s:
            return True
        elif len(s) == 1:
            return False
        stack = []
        pairs_map = ")":"(", "]":"[", "":""
        for x in s:
            if x not in pairs_map:
                stack.append(x)
            elif stack and stack.pop(-1) == pairs_map[x]:
                 continue
            else:
                 return False
        return not stack

你也可以通过Leetcode 在线OJ对此题进行训练。

1.2.2 迷宫问题

迷宫问题描述为，给定一组由可通过和不可通过的方块组成的迷宫，其中有一个位置称之为入口，一个位置为出口，程序需要判断迷宫能否找到一条从入口到出口的路径。

给定一个迷宫如下图，我们直观看下如何搜索路径的，图中蓝色代表入口，红色代表出口，绿色代表路径:

上图时能找到路径的情况，当路径不存在时，程序搜索过程可能如下图所示:

一种简单的解决方案可以描述为:

1) 初始化时 入口节点压入堆栈 
2) 取出栈顶元素，如果当前元素为出口，则成功找到路径；
否则探测当前节点的4个方向，如果找到一个可通过的相邻位置，则这个位置入栈；
若没有找到相邻可通过位置，则当前元素出栈（相当于回退一步，重新找出路）
，如果栈不空则继续步骤2，否则寻找路径失败。

迷宫这种方块布局，我们可以称之为地图，地图可以从文件读取，或者在程序中动态生成，
假设我们从文件读取地图，上图中的地图文件如下:

1111111111
1I01000101
1001000101
1000011001
1011100001
1000100001
1010001001
1011101101
11000000O1
1111111111

我们用’1’代表不可通行，’I’代表入口，’O’代表出口，’0’代表可通过区域。则可以定义每个地图节点如下:

class MazeCellNode(object):
    MAX_TRY_DIR = 3
    MIN_TRY_DIR = 0

    def __init__(self, pos, content):
        self.pos = pos
        self.content = content
        self.try_dir = MazeCellNode.MAX_TRY_DIR

    def __str__(self):
        return str(self.pos)

    def __repr__(self):
        return self.__str__()

    def is_block_cell(self):
        return self.content == "1"

    def is_exit_cell(self):
        return self.content == "O"

    def is_enter_cell(self):
        return self.content == "I"

我们的这种使用堆栈来保存上一步走过的节点，然后在尝试相邻节点失败后，
又退回当前节点，继续寻找可用相邻节点的思路，正是利用了栈的第二个特点，
对前面的状态具有记忆性，可以在将来某个时刻回溯回来，继续使用这个状态信息。

定义数据成员:

self.mazeData = []   # 保存地图节点数据
self.path = []    # 最终路径
self.enter_pos = None  # 入口位置
self.dimension = None  # 地图维度

根据上述算法描述，可以给出寻找路径的算法使用栈的实现版本：

def get_path_using_stack(self):
        if not self.mazeData or not self.dimension:
            return None
        self.path = [self.enter_pos]
        while self.path:
            cell_node = self.__get_cell_node__(self.path[-1])
            if cell_node.is_exit_cell():
                return self.path
            else:
                neighbor_pos = self.__try_next_pos__(cell_node)
                if not neighbor_pos:   # 相邻位置已经都尝试过了 则从路径中移除
                    self.path.pop()
                else:
                    self.path.append(neighbor_pos)    # 未访问过且有效则加入路径
        return None

上面是迷宫问题利用栈的解决方法，实际上使用递归(递归函数是一类直接或者通过其他函数间接调用自身的函数。)也可以实现，在下文我们将看到，递归的本质是利用了系统栈来模拟我们显式使用的栈来解决问题。在阅读完下节后，迷宫问题的递归版本，可以留给你们自己实现。

另一方面，上面的图中，可视化路径搜索过程，使用了Python的 turtle库，利用这个库可以做一些酷酷的可视化效果，例如下面是利用turtle库绘制的奥运五环旗:

感兴趣地可以从我的github下载上述程序代码和查看学习资源。

上述迷宫算法中的一个缺点是，尝试路径的方向对结果有影响，
同时这种暴力尝试也造成了很大时间开销，在后面我们还会花时间深入讨论迷宫问题的其他解决方法。

1.2.3 递归和程序调用堆栈

递归算法通过调用递归函数实现，递归函数是一类直接或者通过其他函数间接调用自身的函数。要支持递归算法，系统必须实现了程序的调用堆栈。
例如下面计算阶乘的递归函数定义如下:

def factorial(x):
    if x <= 1:
        return 1
    else:
        return x * factorial(x-1)

在计算factorial(5)时程序将利用相同的函数计算出factorial(4)， factorial(3)，factorial(2)，factorial(1)，这个过程是这个递归函数自己调用自己的过程。下完将对这个过程进一步说明。

为了理解上述递归调用，一种方式是通过分析调用堆栈来理解。在高级语言编写的程序中，调用函数和被调用函数之间的链接及信息交换通过栈来进行。通常，在运行被调用函数之前，系统需要做3件事，包括(参考自《数据结构》 严蔚敏 吴伟明 清华大学出版社):

• 将所有的实在参数、返回地址等信息传递给被调用函数保存
• 为被调用函数的局部变量分配存储区
• 将控制转移到被调用函数的入口

从被调用函数返回调用函数之前，系统也要完成3件事：

• 保存被调用函数的计算结果
• 释放被调用函数的数据区
• 依照被调函数保存的返回地址将控制转移到调用函数

归纳起来，就是函数调用的过程中处理要素包括：函数控制权的转接工作（利用函数入口地址和返回地址），局部变量的空间分配工作，实参和形参的传递，函数的返回结果传递。

一个函数的状态由一个5元组决定,即function(入口地址，返回地址，形参值，局部变量值，返回值)。保存所有这些信息的数据区称为活动记录（activation record）或者叫做栈帧(stack frame),它是在运行时栈上分配空间的。活动记录，在函数开始执行的时候得到动态分配的空间，在函数退出的时候就释放其空间。一般程序都有一个全局入口，这个函数称为main函数，main函数的的活动记录比其他活动记录生命周期都要长，当程序退出时活动记录才释放。

这里借助Python的inspect模块来监听函数调用过程，结合Python turtle模块，简单的可视化了这个调用过程，将这个类封装在我们的类DebugHelper中，可以从我的github下载这个辅助调试类。

使用DebugHelper类，重新调整代码，书写了stackFrame.py程序如下:

#!/usr/bin/env python
# encoding: utf-8

import sys
from DebugHelper import *


def factorial(x):
    if x <= 1:
        return 1
    else:
        return x * factorial(x-1)


def main():
    print(factorial(5))
    return 1


if __name__ == "__main__":
    DebugHelper.init()
    sys.settrace(DebugHelper.trace_calls)
    main()

在上述调用过程中，系统的堆栈辅助完成了函数的递归调用过程，这个过程实际上有两个阶段，一个阶段为了计算5的阶乘的入栈操作，另一个阶段是计算出1的阶乘后的出栈操作。整个计算过程栈帧的入栈和出栈操作，如下图所示:

通过上图我们看到了递归函数，借助栈帧实现了递归调用，这也是栈的一个重要应用。上面的递归程序只是一个简单例子，后面还会详细介绍递归算法应用例子和设计思路。

本节我们熟悉了常见数据结构中的栈结构，下次我们将学习队列结构，再会。