（梯度下降法）作业

Posted 2022-11-28 小龙呀

第三题程序和结果：

import numpy as np
from sympy import *
import math
import matplotlib.pyplot as plt

# 定义符号
x1, x2, t = symbols('x1, x2, t')  # sympy 符号数学相当于代数式

def func():
    # 自定义一个函数
    return 0.5 * pow(x1, 2) + pow(x2, 2)

def grad(data):
    # 求梯度向量,data=[data1, data2]
    f = func()
    grad_vec = [diff(f, x1), diff(f, x2)]  # 求偏导数,梯度向量
    grad = []
    for item in grad_vec:
        grad.append(item.subs(x1, data[0]).subs(x2, data[1]))  # subs(a,b)将a替换为b
    return grad

def grad_len(grad):
    # 梯度向量的模长
    vec_len = math.sqrt(pow(grad[0], 2) + pow(grad[1], 2))
    return vec_len

def zhudian(f):
    # 求得min(t)的驻点
    t_diff = diff(f)
    t_min = solve(t_diff)
    return t_min

def main(X0, theta):
    f = func()
    grad_vec = grad(X0)  # 偏导数的值
    grad_length = grad_len(grad_vec)  # 梯度向量的模长
    k = 0
    data_x = [0]
    data_y = [0]
    while grad_length > theta:  # 迭代的终止条件
        k += 1
        p = -np.array(grad_vec)
        # 迭代
        X = np.array(X0) + t * p
        t_func = f.subs(x1, X[0]).subs(x2, X[1])
        t_min = zhudian(t_func)  # 驻点
        X0 = np.array(X0) + t_min * p
        grad_vec = grad(X0)
        grad_length = grad_len(grad_vec)
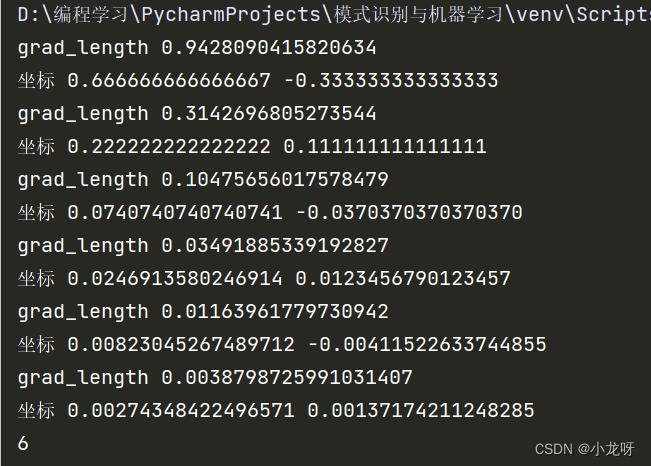
        print('grad_length', grad_length)
        print('坐标', X0[0], X0[1])
        data_x.append(X0[0])
        data_y.append(X0[1])

    print(k)
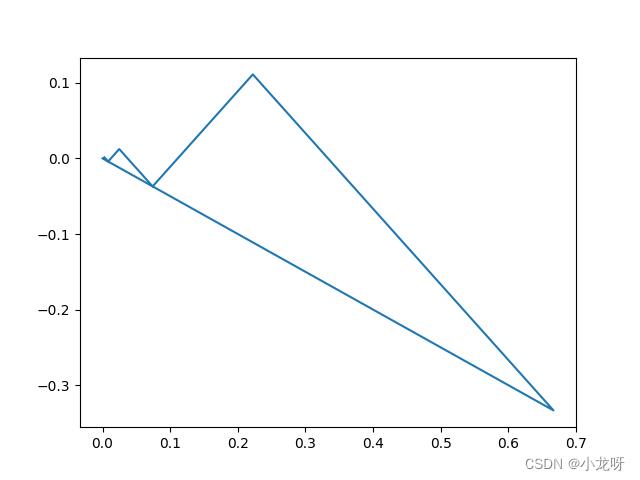
    plt.plot(data_x, data_y)
    plt.show()

if __name__ == '__main__':
    # 给定初始迭代点和阈值
    main([2, 1], 0.01)

本文内容参考：https://blog.csdn.net/qq_32426313/article/details/102711648?spm=1001.2014.3001.5506
如有错误或者不足之处，欢迎大家留言指正！