最优化所需基础知识-第四节:保凸的运算
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最优化所需基础知识-第四节:保凸的运算相关的知识,希望对你有一定的参考价值。
文章目录
保凸运算:简单来说,保凸运算是指原来的集合 C C C是一个凸集,然后让这个凸集 C C C经过一些变换让其仍然为凸集,也即利用凸集构造凸集。保凸运算包括以下三个方面
①:交集是保凸的
- 这一点在“凸集的性质”中已有说明
②:仿射变换是保凸的,包括
- 缩放和移位是凸的
- 两个凸集的和是凸的
- 两个凸集的直积是凸的
- 线性矩阵不等式的解是凸的
③:透视变换是保凸的
- 线段经过透视变换后是凸的
- 凸集的反透视变换仍是凸的
④:分式线性变换是保凸的
一:仿射变换的保凸性
(1)仿射变换的保凸性
仿射变换的保凸性:假设 f : R n → R m f:\\R^n\\rightarrow\\R^m f:Rn→Rm是仿射变换( x ∈ R n x\\in\\R^n x∈Rn、 f ( x ) ∈ R m f(x)\\in\\R^m f(x)∈Rm),即 f ( x ) = A x + b f(x)=Ax+b f(x)=Ax+b(也即仿射变换是线性函数和常量的组合,其中 A ∈ R m × n A\\in \\R^m×n A∈Rm×n、 b ∈ R m b\\in\\R^m b∈Rm、 A x ∈ R m × 1 Ax\\in\\R^m×1 Ax∈Rm×1),则
- 凸集在 f f f下的像(image)是凸集: S ⊆ R n S\\subseteq R^n S⊆Rn是凸集=> f ( S ) = f ( x ) ∣ x ∈ S f(S)=\\f(x)|x\\in S\\ f(S)=f(x)∣x∈S是凸集
- 凸集在 f f f下的原像是凸集: C ⊆ R m C\\subseteq R^m C⊆Rm是凸集=> f − 1 ( C ) = x ∣ f ( x ) ∈ C f^-1(C)=\\x|f(x)\\in C\\ f−1(C)=x∣f(x)∈C是凸集
例题: 设 x 1 , x 2 ∈ S x_1, x_2\\in S x1,x2∈S( S S S为凸集), θ ∈ [ 0 , 1 ] \\theta\\in [0,1] θ∈[0,1],则有凸组合 θ x 1 + ( 1 − θ ) x 2 ∈ S \\theta x_1+(1-\\theta)x_2 \\in S θx1+(1−θ)x2∈S;现证明经仿射变换 f f f下所形成的集合 f ( x ) f(x) f(x)为凸集
- 也即证明:对于 x 1 , x 2 x_1, x_2 x1,x2,有 f ( x 1 ) , f ( x 2 ) ∈ f f(x_1),f(x_2)\\in f f(x1),f(x2)∈f,有 θ ∈ [ 0 , 1 ] \\theta\\in [0,1] θ∈[0,1],是否有 θ f ( x 1 ) + ( 1 − θ ) f ( x 2 ) ∈ f \\theta f(x_1)+(1-\\theta)f(x_2) \\in f θf(x1)+(1−θ)f(x2)∈f成立
- 证明:由于 f ( x ) = A x + b f(x)=Ax+b f(x)=Ax+b,故上上式可转换为 θ ( A x 1 + b ) + ( 1 − θ ) ( A x 2 + b ) = A [ θ x 1 + ( 1 − θ ) x 2 ] + b ( θ ) + ( 1 − θ ) = A [ θ x 1 + ( 1 − θ ) x 2 ] + b \\theta(Ax_1+b)+(1-\\theta)(Ax_2+b)=A[\\theta x_1+(1-\\theta)x_2]+b(\\theta)+(1-\\theta)=A[\\theta x_1+(1-\\theta)x_2]+b θ(Ax1+b)+(1−θ)(Ax2+b)=A[θx1+(1−θ)x2]+b(θ)+(1−θ)=A[θx1+(1−θ)x2]+b,由于 θ x 1 + ( 1 − θ ) x 2 ∈ S \\theta x_1+(1-\\theta)x_2\\in S θx1+(1−θ)x2∈S,故 A [ θ x 1 + ( 1 − θ ) x 2 ] + b ∈ f A[\\theta x_1+(1-\\theta)x_2]+b\\in f A[θx1+(1−θ)x2]+b∈f
仿射变换也可通过下面的例子理解
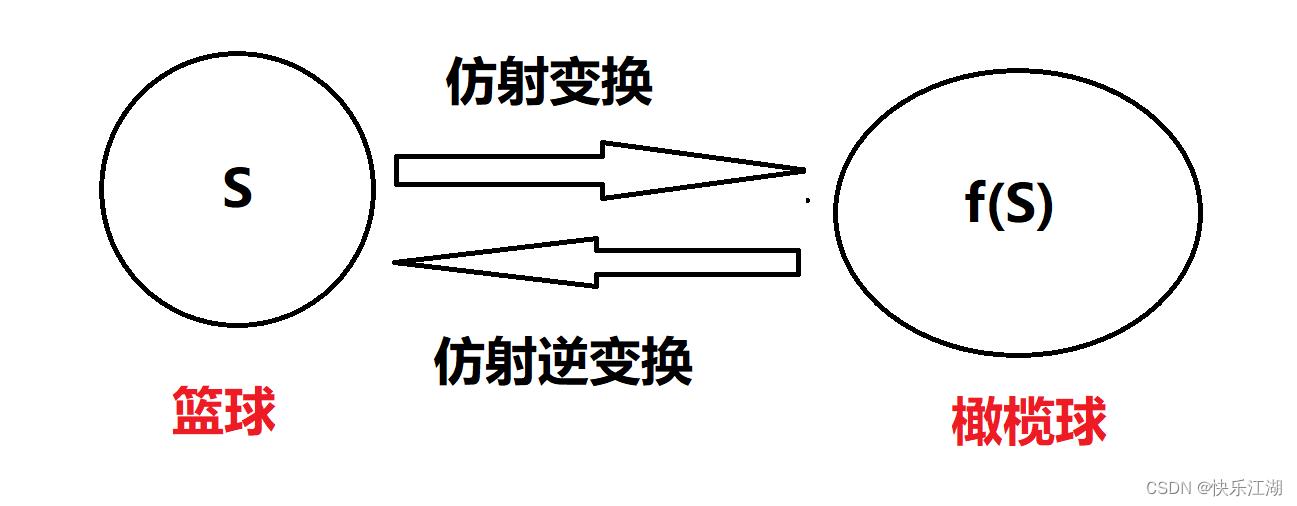
(2)例子
缩放和移位是保凸的:如果 S ⊆ R n S \\subseteq R^n S⊆Rn是凸集, α ∈ R \\alpha \\in R α∈R, a ∈ R a \\in R a∈R,那么缩放和移位后的 α S \\alpha S αS和 S + a S+a S+a也是凸集
- α S = α x ∣ x ∈ S \\alpha S=\\\\alpha x|x \\in S\\ αS=αx∣x∈S
- S + a = x + a ∣ x ∈ S S+a=\\x +a |x \\in S\\ S+a=x+a∣x∈S
两个凸集的和是凸的:两个集合的和被定义为
S 1 + S 2 = x + y ∣ x ∈ S 1 , y ∈ S 2 S_1+S_2=\\x+y | x\\in S_1, y\\in S_2\\ S以上是关于最优化所需基础知识-第四节:保凸的运算的主要内容,如果未能解决你的问题,请参考以下文章
凸函数复合保凸,一般复合,特殊复合(复合仿射映射),各自的保凸条件
(计算机组成原理)第二章数据的表示和运算-第四节1:算数逻辑单元和电路基本知识以及基本逻辑运算和全加器还有串行并行加法器