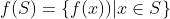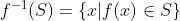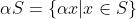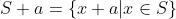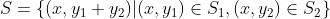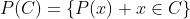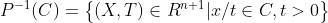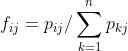凸优化——保凸运算

Posted 2021-12-29 码丽莲梦露

        本文将描述一些保凸运算，利用它们，我们可以从凸集构造出其他凸集。

目录

1 交集

2 仿射函数

3 线性分式及透视函数

 3.1线性分式函数

---

1 交集

        交集运算是保凸的：如果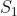和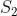是凸集。这个性质可以扩展到无穷个集合的交：

如果对于任意都是凸的，那么也是凸集。

例：多面体是半平面和超平面的交集（它们都是凸集），因而是凸的。

2 仿射函数

        函数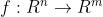是仿射的，如果它是一个线性函数和一个常数的和，即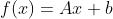

的形式，其中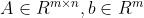。假设 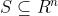是凸的，并且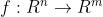是仿射函数。那么，S在f下的象：

 也是凸的，原象为：

两个简单的例子：伸缩和平移：

两个集合的和可以定义为：

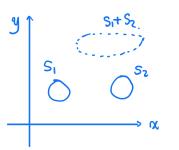
如果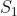和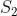是凸集，那么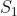+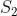是凸的，那么其直积或Cartesian乘积：

 

也是凸集，也可以考虑，的部分和，定义为：

凸集的部分和也是凸集。

3 线性分式及透视函数

透视函数

        我们定义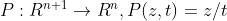为透视函数，其定义域为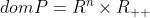。透视函数对向量进行伸缩，或称为规范化，使得最后一维分量为1并舍弃之。

用小孔成像解释透视函数：

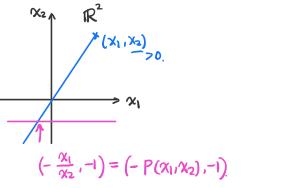
 如果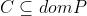是凸集，那么它的象：

 也是凸集。结论很直观：通过小孔观察一个凸的物体，得到的凸的象，证明如下：

 一个凸集的透视函数下的原象也是凸的：

 证明如下：

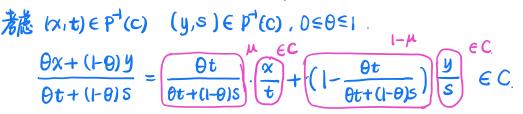
 3.1线性分式函数

        线性分式函数由透视函数和反射函数复合而成

 例：条件概率

设和是分别在1,...,n和1,...,m中取值的随机变量，并且用表示概率.那么条件概率=由下式给出：

因此，可以通过一个线性分式映射从p得到。

可以知道，如果C是一个关于(u,v)的联合密度的凸集，那么相应的u的条件密度（给定v）的集合也是凸集。