（带c++程序）个人对卡尔曼滤波在程序中的实现的理解

Posted 2022-11-03 楚颜a

学习历程

一、学习线性代数的基础知识。卡尔曼滤波涉及行列式和矩阵的知识，需要理解协方差矩阵、行列式的基本运算、矩阵求逆的基本运算，本大一新生对行列式和矩阵一窍不通，先跑去宋浩老师那看了几天行列式和矩阵（实际上如果单纯只是想理解卡尔曼的话不用看得太深入，理解概念和计算方法就行了）。
一开始还挺顺利，学到矩阵乘法的时候有一点混乱，搁置了几天，直到今天做了一道关于矩阵乘法的题目（一开始还不知道这题是关于矩阵乘法的，做出来之后发现好像有种熟悉的感觉，恍然大悟，这不就是矩阵乘法的程序实现嘛！果然，实践出真知）
二、理解卡尔曼滤波的基本原理。看了几个博主讲解的卡尔曼滤波，了解卡尔曼滤波的本质、作用和五个关键的式子，在理解式子时如果头脑混乱就拿起草稿纸跟着博主一步一步走，把容易忘记的量都标注起来
三、理解递归算法的基本概念。跟着教学视频推了一遍公式后就了解得差不多了。

一、什么是卡尔曼滤波

• 卡尔曼滤波本质是一种算法，因为输出变量是输入变量的线性组合，所以我们可以利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计
• 由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程
• 卡尔曼滤波器是最佳的线性滤波器，因为它只能描述状态与状态之间的线性关系
• 数据滤波是去除噪声还原真实数据的一种数据处理技术，卡尔曼滤波在测量方差已知的情况下能够从一系列存在测量噪声的数据中，估计动态系统的状态。由于它便于计算机编程实现，并能够对现场采集的数据进行实时的更新和处理，Kalman滤波是目前应用最为广泛的滤波方法，在通信，导航，制导与控制等多领域得到了较好的应用。
• 线性关系可以写成矩阵的形式

二、卡尔曼滤波的五个关键公式

卡尔曼滤波器学习：卡尔曼滤波器的原理以及在matlab中的实现

小汽车模型：

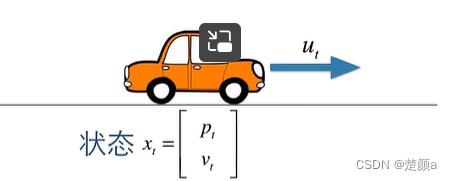
公式一（状态预测公式）：

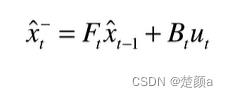
公式二（噪声协方差矩阵传递）：

公式三（观测矩阵）：

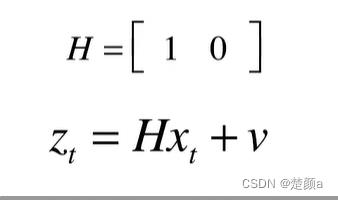
每个测量值都只是真实状态的一种不完全的表现，我们可以从几种不完整的表述，里面推断出真实的状态，而卡尔曼滤波器的数据融合的功能正是在这个测量矩阵中体现出来的

公式四（状态更新）：

把观测量Z和它的噪声协方差矩阵R整合进我们对状态X的估计

• 卡尔曼系数k的两个主要作用：
  一是权衡预测状态协方差P和观察量的协方差矩阵R的大小，来决定我们是相信预测模型多一点还是观察模型多一点。如果相信预测模型多一点，那么残差（实际观测值和预期观测值的差）的权重就会小一点；如果相信观察模型多一点，这个残差的权重就会大一点
  二是把残差的表现形式从观察域转换到状态域。因为观察值Z是一个一维的向量，状态X是一个二维的向量，他们所用的单位甚至描述的特征都有可能是不同的。卡尔曼系数K就是在替我们做用观察值的残差去更新状态值这样一个转换
  在小车这里，K利用速度和位置这两个维度的相关性，从位置的残差里面推算出了速度的残差，从而让我们可以对状态X的两个维度同时进行修正

公式五（噪声协方差矩阵的更新）：

留给下一轮迭代用
在这一轮里状态不确定性是减小的
而在下一轮迭代中，由于传递噪声的引入，不确定性又会增大，卡尔曼滤波器就是在这种不确定性的变化中寻求一种平衡

总结

前两个是根据上一时刻的状态来预测当前时刻的状态，得到的是估计值
后面三个就是用当前的观测值来更新X和P，经过更新后的值就是最佳的观测值

二、递归算法

学习视频：【卡尔曼滤波器】1_递归算法_Recursive Processing
公式推导

k小的时候，1/k值较大，测量结果作用较大；随着k增加，1/k越来越小，测量结果不再重要

总结

递归就是根据上一步的状态来推测当前的状态

三、理解数据融合的基本概念

学习视频：【卡尔曼滤波器】2_数学基础_数据融合_协方差矩阵_状态空间方程_观测器问题

四、卡尔曼滤波程序实现

#include <bits/stdc++.h>
using namespace std;
int n;
struct node

	double pre_X; //上一时刻估计值 
	double X;  //当前估计值 
	double K;   //卡尔曼系数 
	double F;   //状态转移矩阵 
	double H;   //观测矩阵 
	double Q;   //预测模型本身带来的噪声 
	double R;   //噪声协方差矩阵 
	double P;   //协方差矩阵 
kal;
void init()

	kal.pre_X = 0;
	kal.F = 1;
	kal.H = 1;
	kal.Q = 1;
	kal.R = 1;
	kal.P = 1;

double kal_filter(double a)

	kal.pre_X = kal.F * kal.X; //预测下一时刻的值 
	kal.P = kal.F * kal.P * kal.F + kal.Q; //求当前时刻协方差  
	kal.K = kal.P * kal.H / (kal.P * kal.H * kal.H + kal.R); //计算卡尔曼系数 
	kal.X = kal.pre_X + (a - kal.H * kal.pre_X) * kal.K;  //状态更新,此处的a即为输入的观测值 
	kal.P = (1 - kal.K * kal.H) * kal.P; //噪声协方差矩阵的更新 
	//单位矩阵值为1 
	return  kal.X; 

int main()

	cin>>n; //输入迭代次数
	init(); //数据初始化 
    for(int i=1;i<=n;i++)
    
    	double a;
        cin>>a; 
        cout<<kal_filter(a)<<endl;
    
    return 0;