神经网络中常见的激活函数

Posted 2022-10-24 半吊子全栈工匠

深度学习中已经成为了人工智能领域的必备工具，源于人工神经网络的研究，含多个隐藏层的多层感知器就是一种深度学习结构。寻找隐藏层的权重参数和偏置的过程，就是常说的“学习”过程，其遵循的基本原则就是使得网络最终的输出误差最小化。在神经⽹络中，激活函数是必须选择的众多参数之⼀，从而使神经⽹络获得最优的结果和性能。

经常用到的激活函数有哪些呢？如何进行选择呢？

关于激活函数

激活函数（Activation Function），就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端，激活函数将神经网络中将输入信号的总和转换为输出信号。激活函数大多是非线性函数，才能将多层感知机的输出转换为非线性，使得神经网络可以任意逼近任何非线性函数，进而可以应用到众多的非线性模型中。

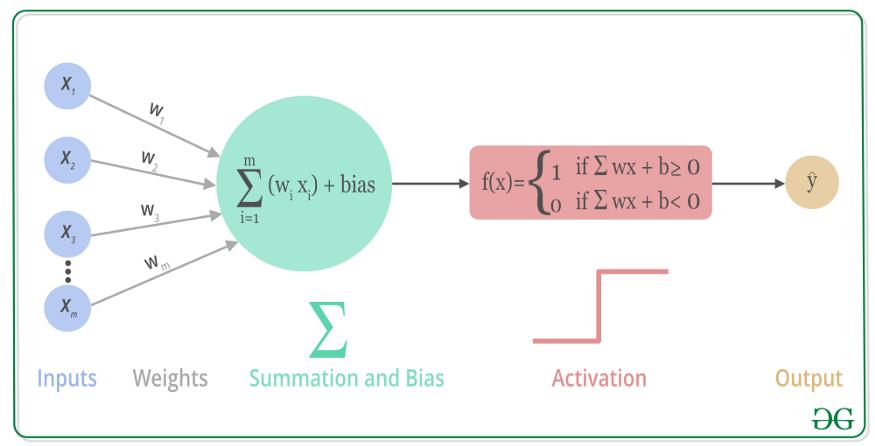
也就是说，非线性激活函数可以创建输入与输出键的复杂映射关系，神经网络也能通过“学习”来更新参数。并且，因为非线性函数的导数与输入有关，从而可以通过向后传播算法计算梯度，也可以构建多层神经网络，以处理复杂问题。

常见的激活函数有用于浅层网络的sigmoid 系列，用于深层网络的ReLU系列，用于递归网络的tanh系列以及Softmax 系列等等。

sigmoid 系列

sigmoid函数也叫Logistic函数，用于隐层神经元输出，能将( − ∞ , + ∞ )的数值映射到(0,1)的区间，当以概率形式表示预测值时，一般使用这个函数。sigmod激活函数的Python 代码如下：

import numpy as np

def sigmoid(x):
    s = 1 / (1 + np.exp(-x))
    return s

函数的图像如下所示：

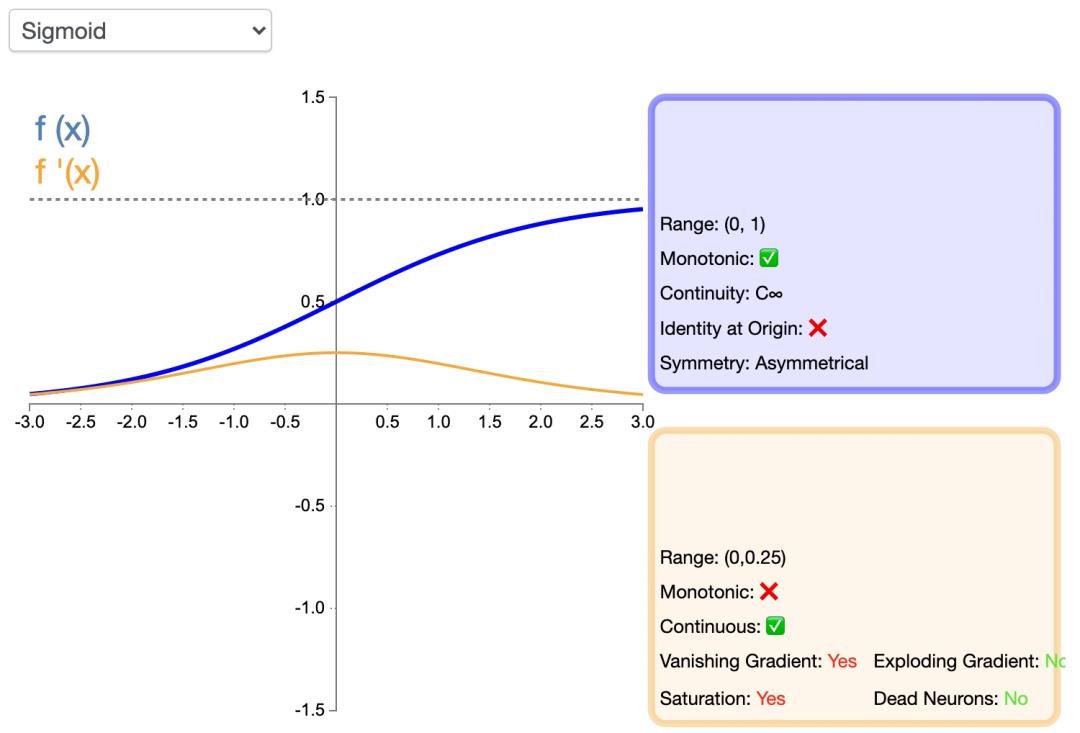
Sigmoid函数的优点在于它可导，并且值域在0到1之间，使得神经元的输出标准化，是神经网络最早采用的激活函数。它的不足也很明显，在增加或减少到一定程度时，函数值变化很小，这就是所谓的“梯度消失”，致使网络的收敛速度变慢，进而耗费计算资源。另外，输出值不是以0为中心，而是0.5。

一般的Sigmoid 函数应用于浅层网络。

HardSigmoid

在Sigmoid的基础上，又有HardSigmoid，因为当输入值趋向无穷大的时候，输出值趋向于1；当输入值趋向无穷小的时候，输出值趋向于0。所以，顾名思义，HardSigmoid是在Sigmoid的基础上，当输入值超过某个范围强行置1和0。HardSigmoid 的python 代码如下：

def Hard_sigmoid(x):
    y = []
    for i in x:
        if i < -2.5:
            y_i = 0
        elif i >= -2.5 and i <= 2.5:
            y_i = 0.2 * i + 0.5
        else:
            y_i = 1
        y.append(y_i)
    return y

HardSigmoid 激活函数的函数图像如下：

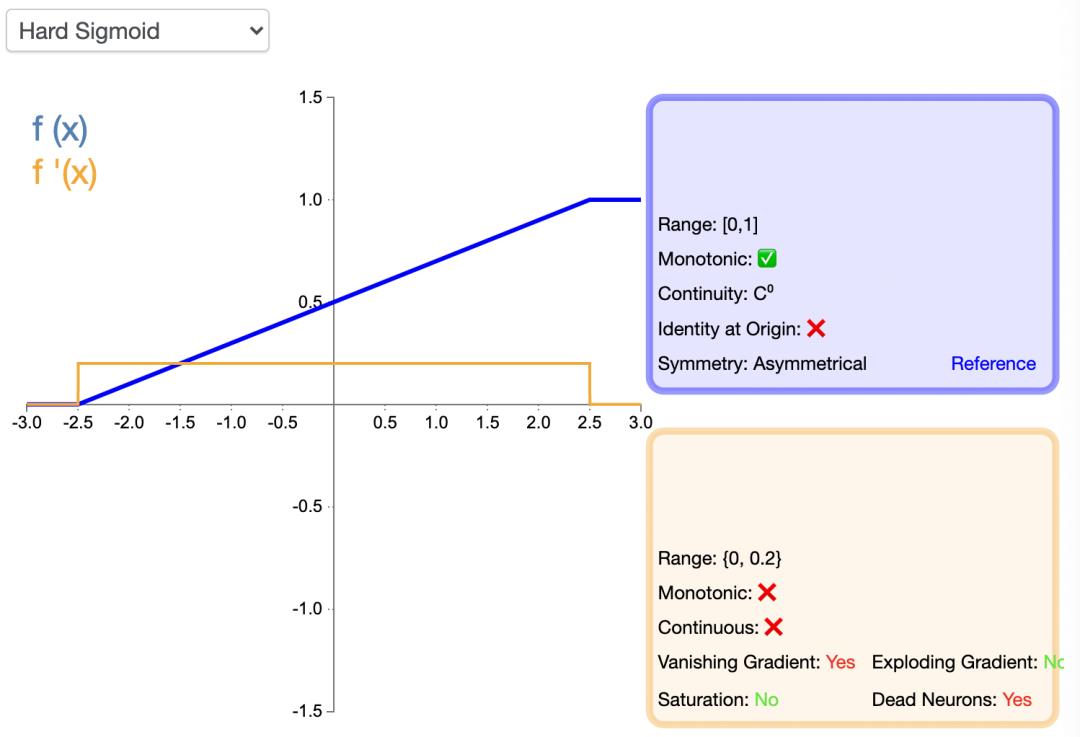
Swish

swish的表达式为：f ( x ) = x ⋅ s i g m o i d ( b x )，python代码如下：

def Swish(x):
    return x / (1 + np.exp(-b*x))

其中b是可学参数， Swish 具备无上界有下界、平滑、非单调的特性。

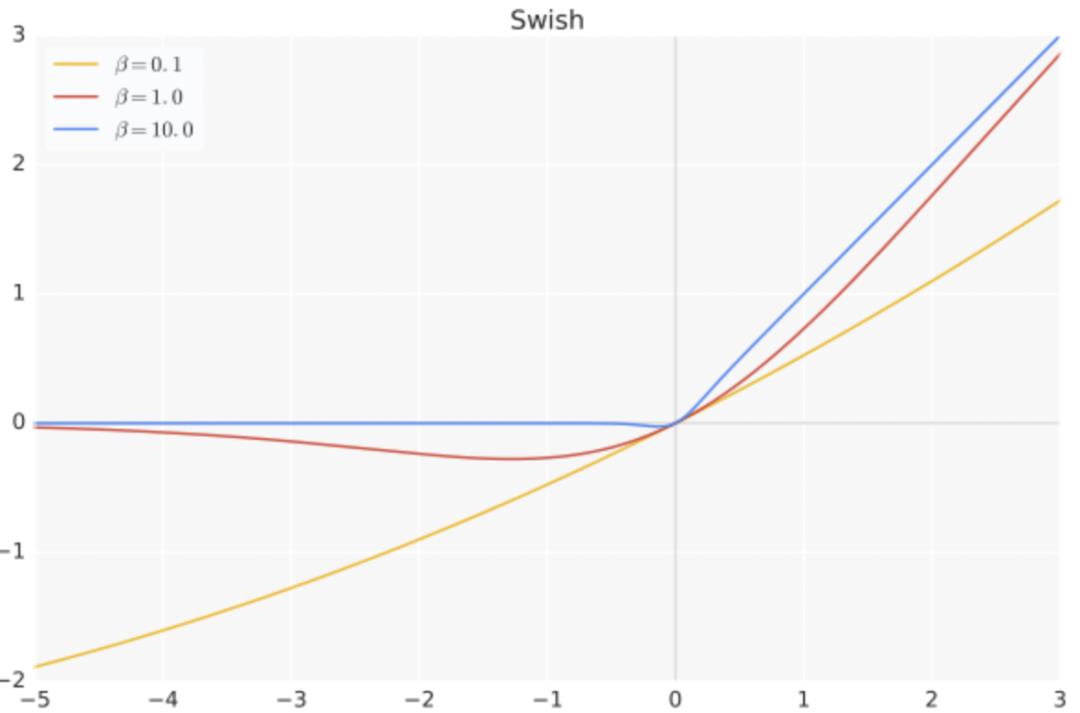
Swish 在深层模型上的效果优于 ReLU。例如，仅仅使用 Swish 单元替换 ReLU 就能把 Mobile NASNetA 在 ImageNet 上的分类准确率提高 0.9%。

maxout

Maxout可以看做是在深度学习网络中加入一层激活函数层,包含一个参数k。这一层相比ReLU,sigmoid等,其特殊之处在于增加了k个神经元,然后输出激活值最大的值。

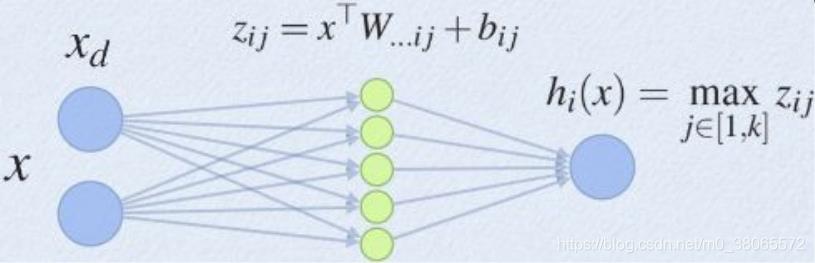
maxout是一个函数逼近器，对于一个标准的MLP网络来说，如果隐藏层的神经元足够多，那么理论上是可以逼近任意的函数的。Maxout的拟合能力非常强，可以拟合任意的凸函数，具有ReLU的所有优点，线性、不饱和性，同时没有ReLU的一些缺点，如神经元的死亡。

Relu系列

Relu （Rectified Linear Unit）称为“线性整流函数”或者“修正线性单元”，通常就直接称为 ReLU 函数，是解决梯度消失问题的方法。将 ReLU 函数引入神经网络时，也引入了很大的稀疏性。然而，由于稀疏性，时间和空间复杂度更低，不涉及成本更高的指数运算，允许网络快速收敛。

尽管Relu看起来像线性函数，但它具有导数函数并允许反向传播，python 代码如下：

import numpy as np

def relu(x):
    s = np.where(x < 0, 0, x)
    return s

ReLU引入了神经元死亡问题，当输入接近零或为负时，函数的梯度变为零，网络将无法执行反向传播，也无法学习，也就是说，网络的大部分分量都永远不会更新，另外，它不能避免梯度爆炸问题。

ReLU是现在DNN模型中比较常用的激活函数。

ELU

指数线性单元激活函数ELU解决了 ReLU 的一些问题，同时也保留了一些好的方面。这种激活函数要选取一个 α 值；常见的取值是在 0.1 到 0.3 之间。但α =0.3时的函数图像如下：

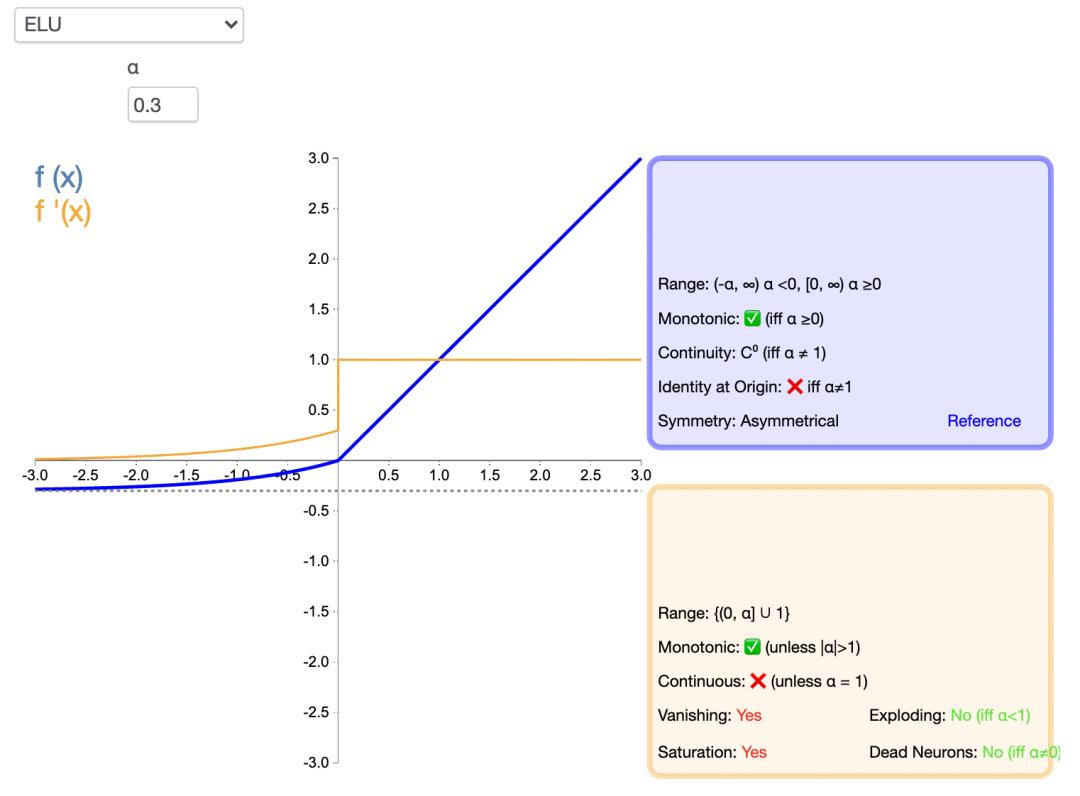
ELU能避免神经元死亡问题，能得到负值输出，这能帮助网络向正确的方向推动权重和偏置变化，在计算梯度时能得到激活，而不是让它们等于 0。ELU 的python 代码如下：

import numpy as np

def elu(x):
    s = np.where(x >= 0, x, α(np.exp(x)-1)
    return s

但是，由于包含了指数运算，计算时间更长，同样无法避免梯度爆炸问题，另外，神经网络不学习 α 值。

Leaky ReLU

渗漏型整流线性单元激活函数也有一个 α 值，通常取值在 0.1 到 0.3 之间。Leaky ReLU 激活函数很常用，相比于 ELU 也有一些缺陷，但比 ReLU 具有一些优势。

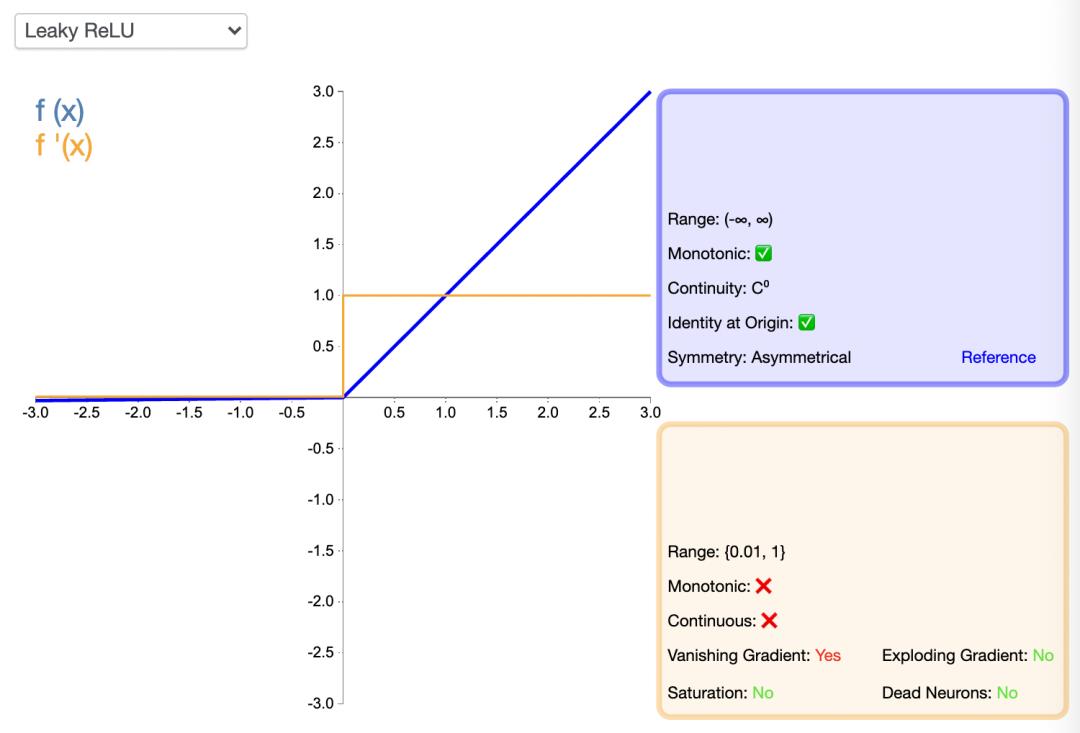
LeakyReLU的负值斜率很小，而不是平坦的斜率。斜率系数需要在训练前确定，即在训练过程中不学习。这种类型的激活函数在可能遇到稀疏梯度的任务中很流行，例如训练生成式对抗网络。

import numpy as np

def lrelu(x):
    s = np.where(x >= 0, x, αx)
    return s

类似 ELU，Leaky ReLU 也能避免死亡 ReLU 问题，因为其在计算导数时允许较小的梯度，由于不包含指数运算，所以计算速度比 ELU 快。

扩展型指数线性单元激活函数（SELU）

SELU 激活能够对神经网络进行自归一化，归一化就是首先减去均值，然后除以标准差。因此，经过归一化之后，网络的组件（权重、偏置和激活）的均值为 0，标准差为 1，而这正是 SELU 激活函数的输出值。通过归一化，网络参数会被初始化一个正态分布。

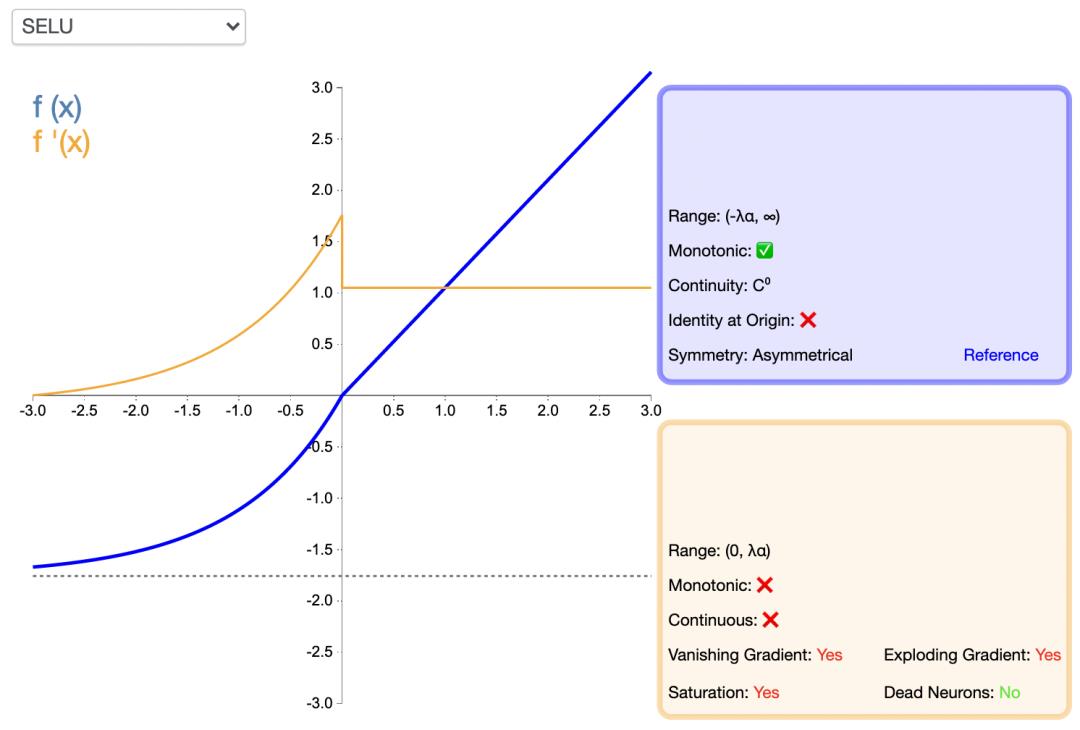
通过归一化，网络参数会被初始化一个正态分布。

def SeLU(x,alpha=1.6732632423543772848170429916717,scale=1.0507009873554804934193349852946):
    y = []
    for i in x:
        if i >= 0:
            y_i = scale * i
        else:
            y_i = scale * alpha * (np.exp(i) - 1)
        y.append(y_i)
    return y

SELU内部归一化的速度比外部归一化快，这意味着网络能更快收敛，而且避免了出现梯度消失或爆炸问题，在CNN或RNN 网络架构中有所应用。

高斯误差线性单元激活函数GELU

GELU是某些函数（比如双曲正切函数 tanh）与近似数值的组合，

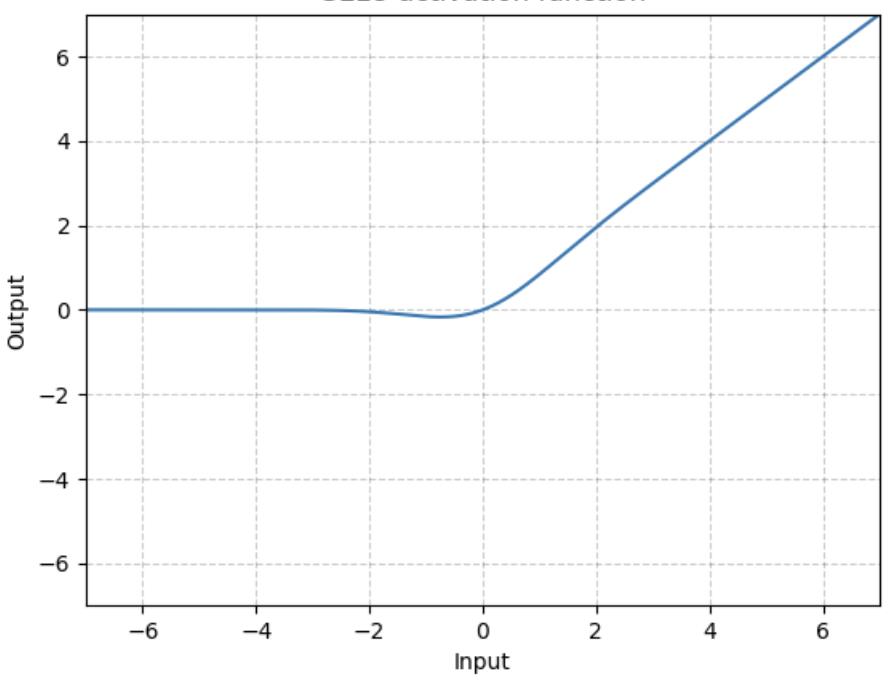
当 x 大于 0 时，输出为 x；但 x=0 到 x=1 的区间除外，这时曲线更偏向于 y 轴。

import numpy as np
def tanh(x):
    s1 = np.exp(x) - np.exp(-x)
    s2 = np.exp(x) + np.exp(-x)
    s = s1 / s2
    return s
gelu = lambda x:0.5 * x * (1 + tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * np.power(x, 3))))

GELU 在NLP 领域有较好表现，尤其在 Transformer 模型中表现最好，能避免梯度消失问题。

tanh系列

tanh

Tanh函数，即双曲正切函数，比sigmoid函数更受欢迎，能为多层神经网络提供更好的性能。

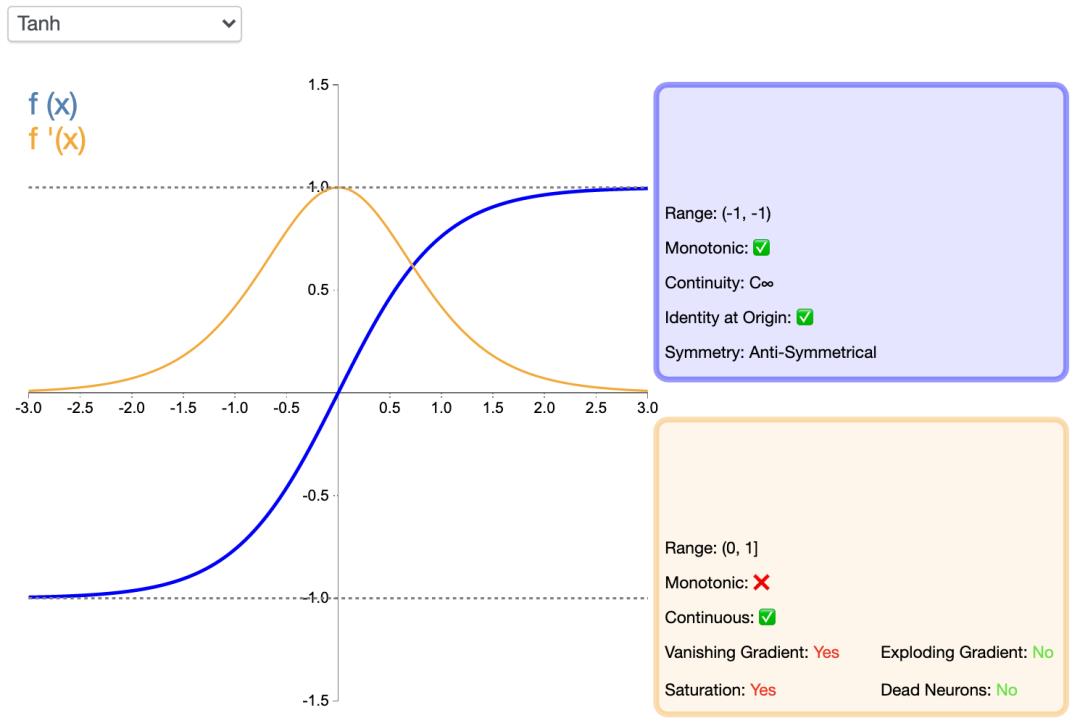
它的输出更多地以零为中心，这有助于加速收敛，尤其是在训练初期。双曲线正切函数的python代码如下：

import numpy as np

def tanh(x):
    s1 = np.exp(x) - np.exp(-x)
    s2 = np.exp(x) + np.exp(-x)
    s = s1 / s2
    return s

Tanh函数的最大优点是输出值以 0为中心，即关于坐标原点对称，分属为正数和负数两大类别，函数及其导数都是单调的，收敛速度比sigmoid快，从而可以减少迭代次数。这使得它具有了Sigmoid函数的优势，又克服了某些不足。但是，“梯度消失”的问题都还存在，进而导致收敛速度变慢。

Tanh 一般用于递归神经网络。

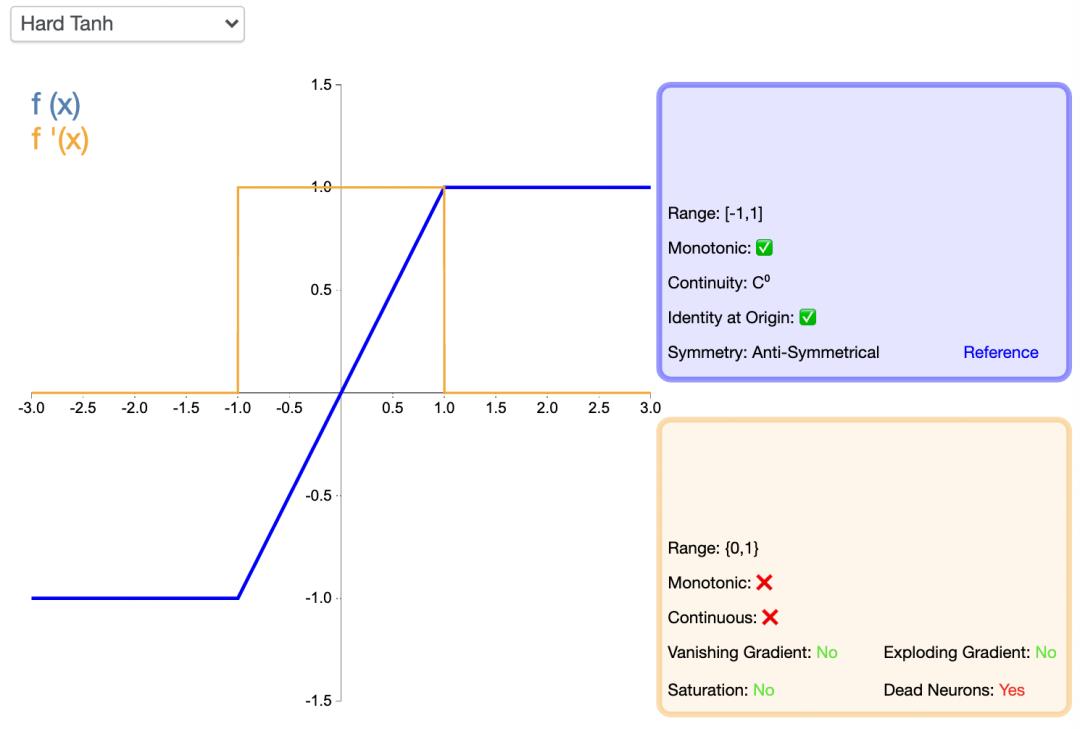
HardTanh

Hardtanh激活函数是Tanh的线性分段近似。相较而言，它更易计算，这使得学习计算的速度更快，尽管首次派生值为零可能导致静默神经元/过慢的学习速率。

TanhShrink

基于Tanh之上，计算输入输出的差值，即为TanhShrink，函数图像如下。

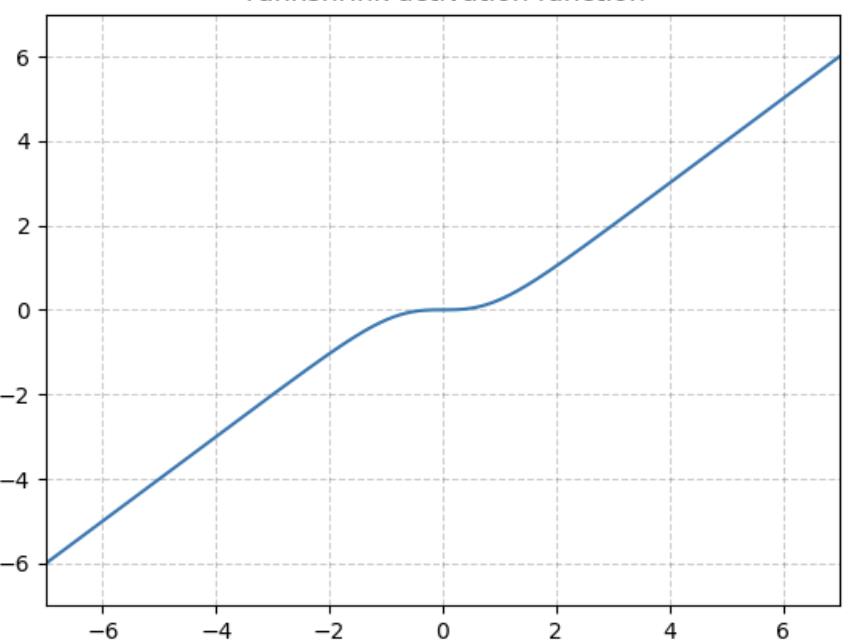
在当输入在0附近时，梯度近乎为0，而在输入极大或极小时，梯度反而为正常梯度。

softmax 系列

Softmax函数比较适合作为多分类模型的激活函数，一般会与交叉熵损失函数相配。

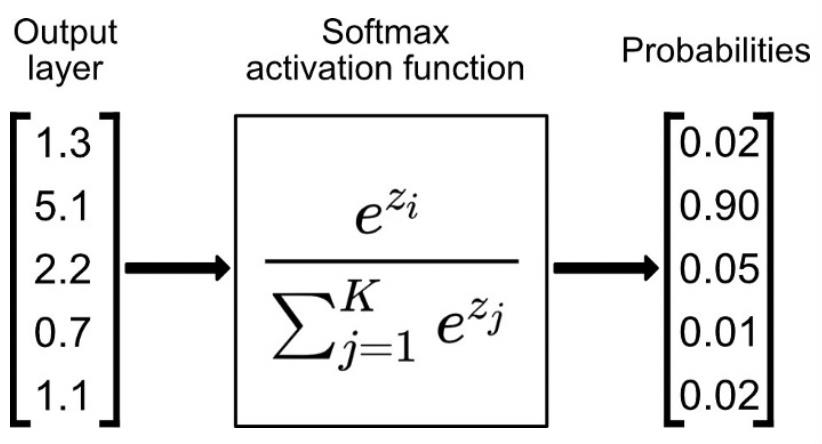
通常，Softmax函数只应用于输出层，把一堆实数的值映射到0-1区间，并且使他们的和为1，可以理解为对应每个类别对应的预测概率。python代码如下：

def softmax(x):
    x_exp = np.exp(x)
    x_sum = np.sum(x_exp, axis=1, keepdims=True)
    s = x_exp / x_sum
    return s

如果某一个zj大过其他z,那这个映射的分量就逼近于1,其他就逼近于0。

Softmax函数用于将输入进行归一化到(0,1)，并且其和为1，普遍应用于分类模型(互斥)的预测概率值。事实上，但凡涉及到概率的地方基本都会用到softmax，典型的就比如attention layer当中，都会使用softmax来计算attention值。

LogSoftMax

 LogSoftmax是基于Softmax函数之上，计算其对应的对数值，范围在(-∞,0)用来计算交叉熵损失函数(根据groundtruth的标签取出对应的值即可)。LogSoftMax 加快了运算速度，提高数据稳定性。

Softmin

Softmin是在Softmax的基础上，做相反变换。Softmin是在Softmax的基础上，做相反变换。  跟softmax类似，输入n维t数据，对它们进行重新缩放使得n维输出的每个元素都在[0, 1]区间内，且和为1。不同的是，softmax是单调递增而softmin是单调递减，意味着softmax操作会使得最大的值在激活操作后依然保持最大，而softmin会使得最小的数在经过了softmin后变成最大值。

激活函数的选择

以终为始，激活函数的选择也是为最终的任务目标服务的。不存在普遍适用各种神经网络的万能的激活函数，在选择激活函数的时候，要考虑不同的条件限制，例如，如果函数可导，求导数的计算难度如何？函数光滑程度如何？输出是否保持标准化？网络的收敛速度如何？等等。

一般地，在用于分类器时，Sigmoid函数及其组合通常效果更好。为了避免梯度消失问题，又需要避免使用Sigmoid和TanH。如果是回归模型，在输出层上可以使用线性激活函数。如果是浅层神经网络，如不超过4层的，可选择使用多种激励函数，没有太大的影响。如果网络中存在大量未激活神经元，可以考虑leaky ReLU函数。

ReLU函数是应用比较广泛的激活函数，可以作为默认选项。深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的所以要尽量选择输出具有zero-centered特点的激活函数以加快模型的收敛速度。

一个经验上的建议是：SELU > ELU > Leaky ReLU > ReLU> tanh > sigmoid，但是，如果网络的体系结构阻止自归一化，那么 ELU 可能是比 SELU 更好的选择。如果速度很重要，Leaky ReLU 将是比慢很多的 ELU 更好的选择。

更重要的是，激活函数仍在发展，需要跟踪业界的最新进展，并勇于探索和创新。

一句话小结

激活函数是神经网络中的重要参数，一般地，Sigmoid 系列用于二分类任务输出层，softmax系列用于多分类任务输出层，tanh系列用于模型隐藏层，Relu系列用于回归任务以及卷积神经网络隐藏层。但事无绝对，而且，新研究的激活函数仍在涌现。

附，reddit上有一张激活函数的图，挺有意思的！

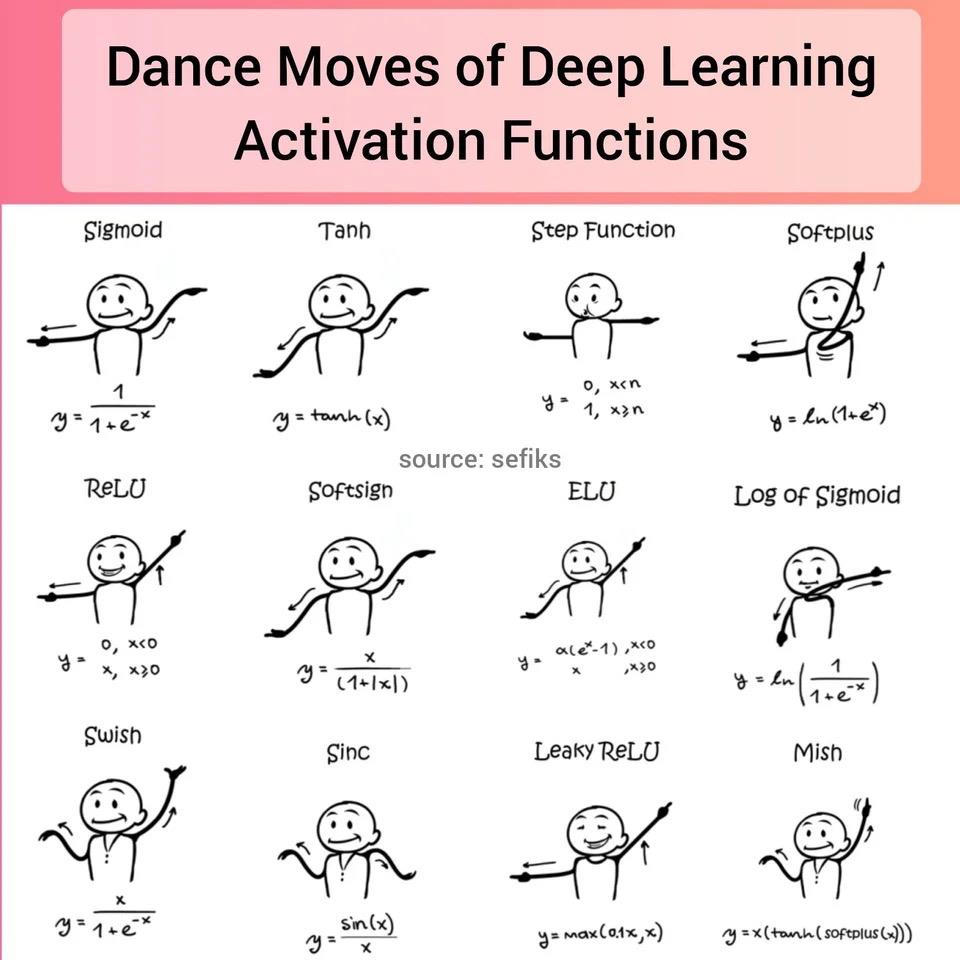
【关联阅读】

• https://dashee87.github.io/deep%20learning/visualising-activation-functions-in-neural-networks/

• 老码农眼中的简明AI
  

• https://en.wikipedia.org/wiki/Activation_function
  

• 感知人工智能操作系统

• 难以捉摸？机器学习模型的可解释性初探
  

• 神经网络加速器的兴起

• 清单管理？面向机器学习中的数据集

• 嵌入式中的人工神经网络

• 老码农的AI漫谈

• 人工智能伦理学的一知半解

• 浅谈人工智能的学习

• 揭秘“语音交互”背后的AI硬核黑科技！

• 机器学习之于IOT浅见

• AI 语音交互开放平台的构建与演进

• AI系统中的偏差与偏见