深度学习神经元介绍

Posted 2022-12-13 赵广陆

目录

• 1 激活函数
• • 1.1 Sigmoid/logistics函数：
  • 1.2 tanh(双曲正切曲线)
  • 1.3 RELU
  • 1.4 LeakReLu
  • 1.5 SoftMax
  • 1.6 其他激活函数
  • 1.7 如何选择激活函数
  • • 1.7.1 隐藏层
    • 1.7.2 输出层
• 2 参数初始化
• • 2.1 随机初始化
  • 2.2 标准初始化
  • 2.3 Xavier初始化
  • 2.4 He初始化

---

1 激活函数

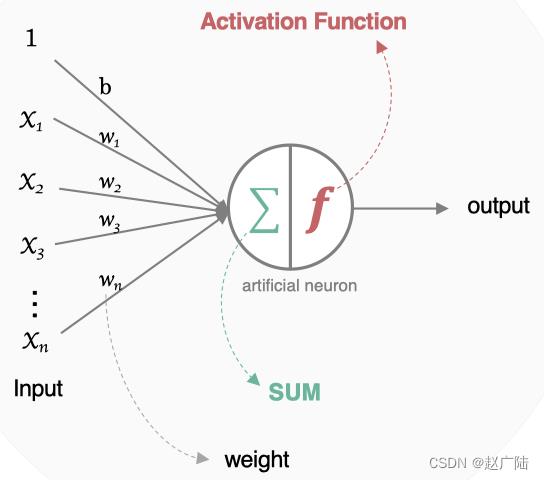
人工神经元接收到一个或多个输入，对他们进行加权并相加，总和通过一个非线性函数产生输出。

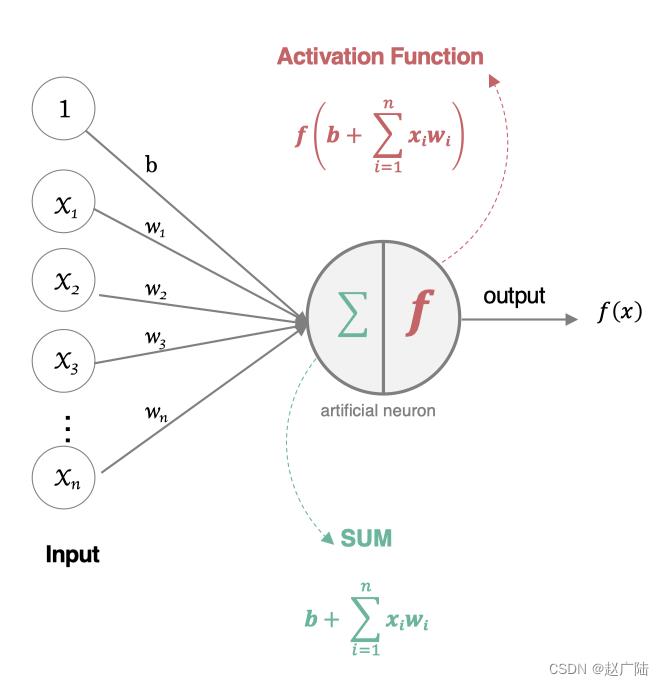
• 所有的输入xi，与相应的权重wi相乘并求和：

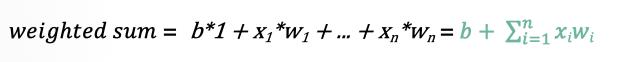
• 将求和结果送入到激活函数中，得到最终的输出结果：

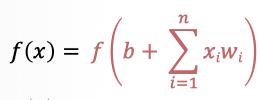
在神经元中引入了激活函数，它的本质是向神经网络中引入非线性因素的，通过激活函数，神经网络就可以拟合各种曲线。如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，引入非线性函数作为激活函数，那输出不再是输入的线性组合，可以逼近任意函数。常用的激活函数有：

1.1 Sigmoid/logistics函数：

数学表达式为：

曲线如下图所示：

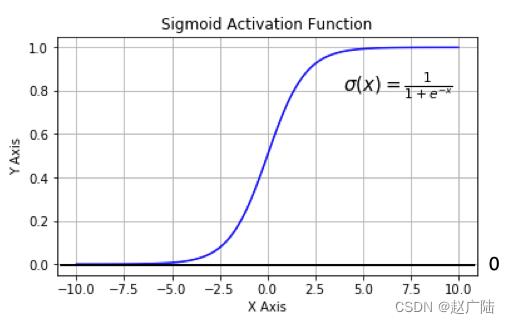
sigmoid 在定义域内处处可导，且两侧导数逐渐趋近于0。如果X的值很大或者很小的时候，那么函数的梯度（函数的斜率）会非常小，在反向传播的过程中，导致了向低层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象。而且，该激活函数并不是以0为中心的，所以在实践中这种激活函数使用的很少。sigmoid函数一般只用于二分类的输出层。

实现方法：

# 导入相应的工具包
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import numpy as np
# 定义x的取值范围
x = np.linspace(-10, 10, 100)
# 直接使用tensorflow实现
y = tf.nn.sigmoid(x)
# 绘图
plt.plot(x,y)
plt.grid()

1.2 tanh(双曲正切曲线)

数学表达式如下：

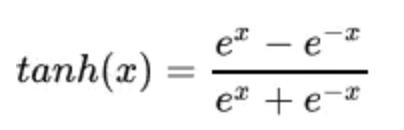
曲线如下图所示：

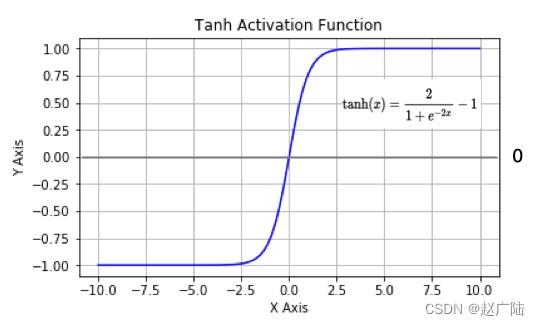
tanh也是一种非常常见的激活函数。与sigmoid相比，它是以0为中心的，使得其收敛速度要比sigmoid快，减少迭代次数。然而，从图中可以看出，tanh两侧的导数也为0，同样会造成梯度消失。

若使用时可在隐藏层使用tanh函数，在输出层使用sigmoid函数。

实现方法为：

# 导入相应的工具包
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import numpy as np
# 定义x的取值范围
x = np.linspace(-10, 10, 100)
# 直接使用tensorflow实现
y = tf.nn.tanh(x)
# 绘图
plt.plot(x,y)
plt.grid()

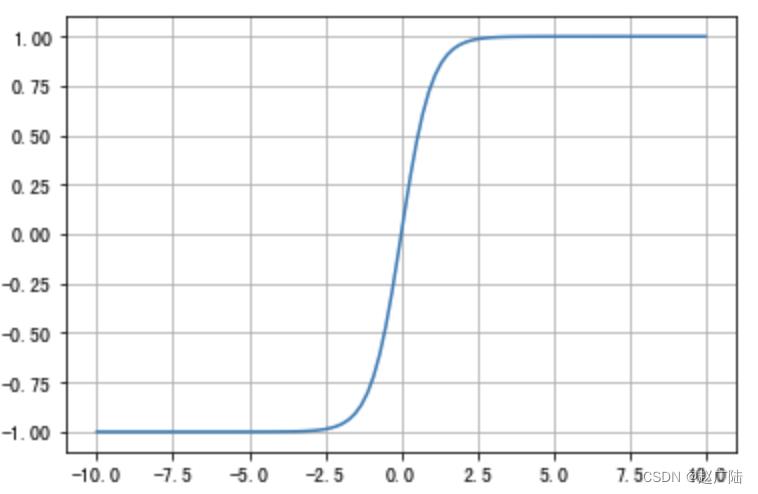
1.3 RELU

数学表达式为：

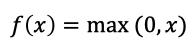
曲线如下图所示：

ReLU是目前最常用的激活函数。 从图中可以看到，当x<0时，ReLU导数为0，而当x>0时，则不存在饱和问题。所以，ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。然而，随着训练的推进，部分输入会落入小于0区域，导致对应权重无法更新。这种现象被称为“神经元死亡”。

与sigmoid相比，RELU的优势是：

• 采用sigmoid函数，计算量大（指数运算），反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。
• sigmoid函数反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。
• Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。

实现方法为：

# 导入相应的工具包
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import numpy as np
# 定义x的取值范围
x = np.linspace(-10, 10, 100)
# 直接使用tensorflow实现
y = tf.nn.relu(x)
# 绘图
plt.plot(x,y)
plt.grid()

1.4 LeakReLu

该激活函数是对RELU的改进，数学表达式为：

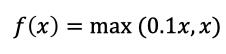
曲线如下所示：

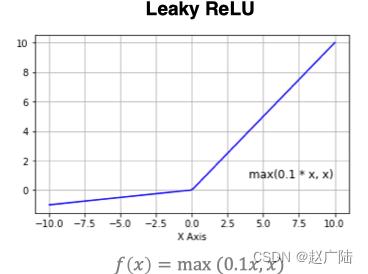
实现方法为：

# 导入相应的工具包
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import numpy as np
# 定义x的取值范围
x = np.linspace(-10, 10, 100)
# 直接使用tensorflow实现
y = tf.nn.leaky_relu(x)
# 绘图
plt.plot(x,y)
plt.grid()

1.5 SoftMax

softmax用于多分类过程中，它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。

计算方法如下图所示：

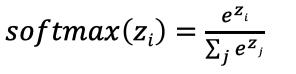
使用方法：

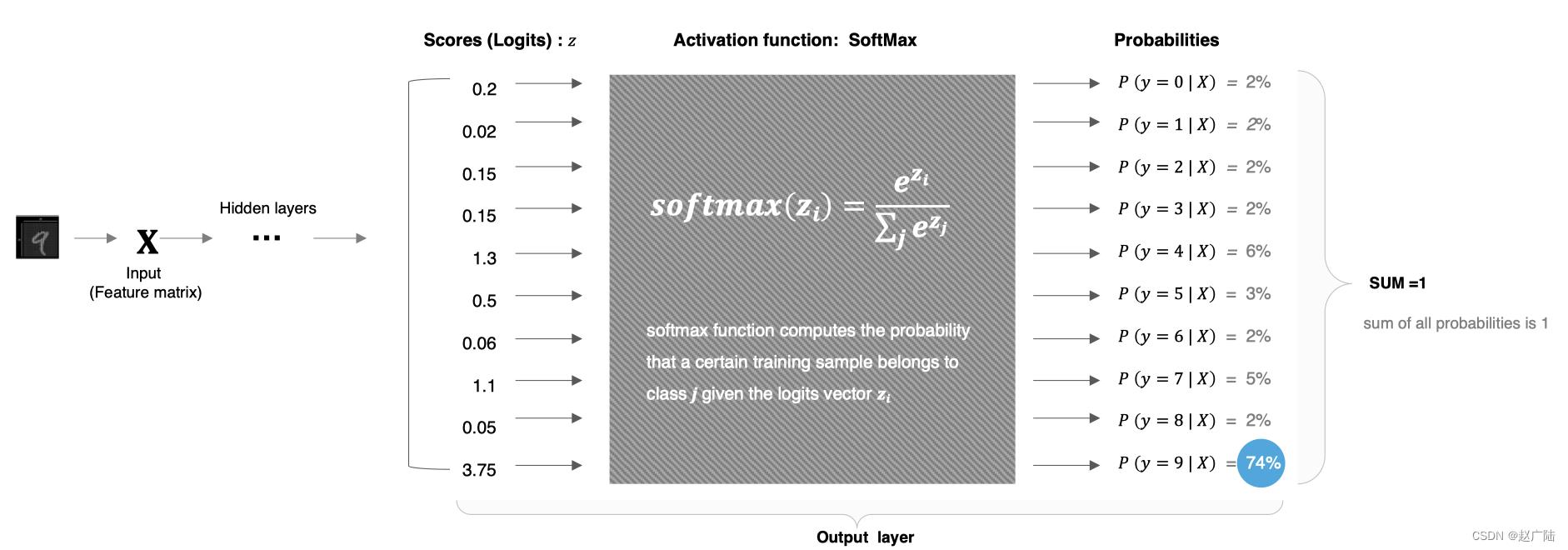
softmax直白来说就是将网络输出的logits通过softmax函数，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们将它理解成概率，选取概率最大（也就是值对应最大的）接点，作为我们的预测目标类别。

实现，以上图中数字9的分类结果为例给大家进行演示：

# 导入相应的工具包
import tensorflow as tf
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import numpy as np
# 数字中的score
x = tf.constant([0.2,0.02,0.15,1.3,0.5,0.06,1.1,0.05,3.75])
# 将其送入到softmax中计算分类结果
y = tf.nn.softmax(x) 
# 将结果进行打印
print(y)

分类结果为：

tf.Tensor(
[0.02167152 0.01810157 0.02061459 0.06510484 0.02925349 0.01884031
 0.05330333 0.01865285 0.75445753], shape=(9,), dtype=float32)

1.6 其他激活函数

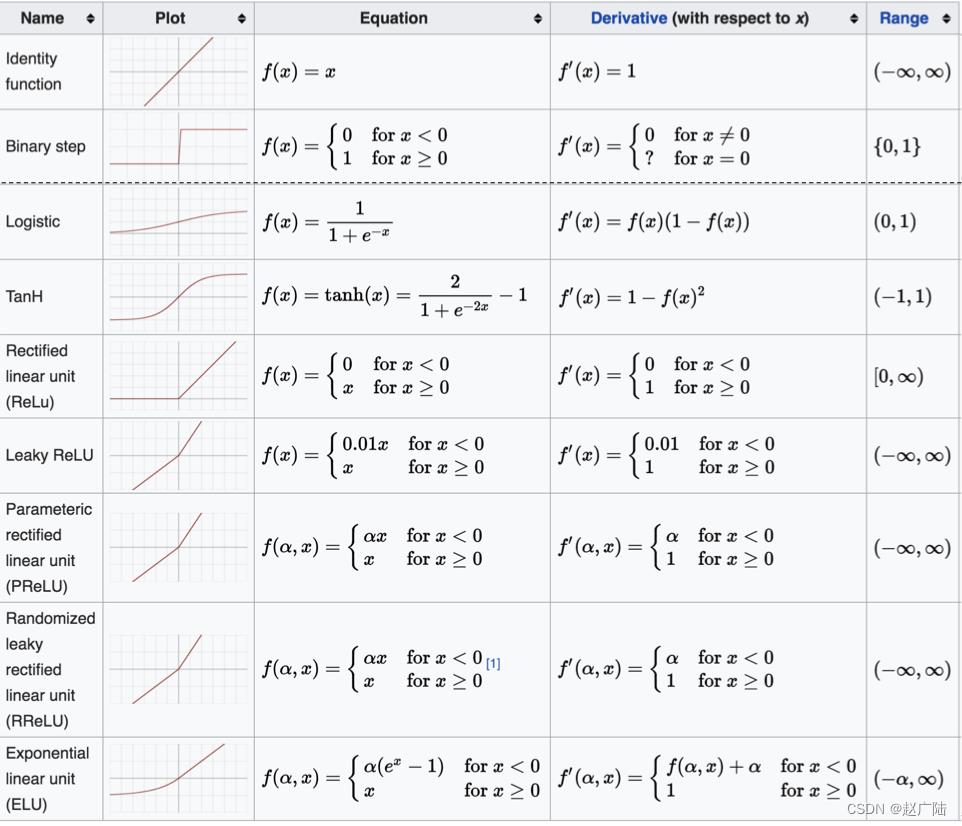
1.7 如何选择激活函数

1.7.1 隐藏层

• 优先选择RELU激活函数
• 如果ReLu效果不好，那么尝试其他激活，如Leaky ReLu等。
• 如果你使用了Relu， 需要注意一下Dead Relu问题， 避免出现大的梯度从而导致过多的神经元死亡。
• 不要使用sigmoid激活函数，可以尝试使用tanh激活函数

1.7.2 输出层

• 二分类问题选择sigmoid激活函数
• 多分类问题选择softmax激活函数
• 回归问题选择identity激活函数

2 参数初始化

对于某一个神经元来说，需要初始化的参数有两类：一类是权重W，还有一类是偏置b,偏置b初始化为0即可。而权重W的初始化比较重要，我们着重来介绍常见的初始化方式。

2.1 随机初始化

随机初始化从均值为0，标准差是1的高斯分布中取样，使用一些很小的值对参数W进行初始化。

2.2 标准初始化

权重参数初始化从区间均匀随机取值。即在(-1/√d,1/√d)均匀分布中生成当前神经元的权重，其中d为每个神经元的输入数量。

2.3 Xavier初始化

该方法的基本思想是各层的激活值和梯度的方差在传播过程中保持一致，也叫做Glorot初始化。在tf.keras中实现的方法有两种：

• 正态化Xavier初始化：

Glorot 正态分布初始化器，也称为 Xavier 正态分布初始化器。它从以 0 为中心，标准差为 stddev = sqrt(2 / (fan_in + fan_out)) 的正态分布中抽取样本， 其中 fan_in 是输入神经元的个数， fan_out 是输出的神经元个数。

实现方法为：

# 导入工具包
import tensorflow as tf
# 进行实例化
initializer = tf.keras.initializers.glorot_normal()
# 采样得到权重值
values = initializer(shape=(9, 1))
# 打印结果
print(values)

输出结果为：

tf.Tensor(
[[ 0.71967787]
 [ 0.56188506]
 [-0.7327265 ]
 [-0.05581591]
 [-0.05519835]
 [ 0.11283273]
 [ 0.8377778 ]
 [ 0.5832906 ]
 [ 0.10221979]], shape=(9, 1), dtype=float32)

• 标准化Xavier初始化

Glorot 均匀分布初始化器，也称为 Xavier 均匀分布初始化器。它从 [-limit，limit] 中的均匀分布中抽取样本， 其中 limit 是 sqrt(6 / (fan_in + fan_out))， 其中 fan_in 是输入神经元的个数， fan_out 是输出的神经元个数。

# 导入工具包
import tensorflow as tf
# 进行实例化
initializer = tf.keras.initializers.glorot_uniform()
# 采样得到权重值
values = initializer(shape=(9, 1))
# 打印结果
print(values)

输出结果为：

tf.Tensor(
[[-0.59119344]
 [ 0.06239486]
 [ 0.65161395]
 [-0.30347362]
 [-0.5407096 ]
 [ 0.35138106]
 [ 0.41150713]
 [ 0.32143414]
 [-0.57354397]], shape=(9, 1), dtype=float32)

2.4 He初始化

he初始化，也称为Kaiming初始化，出自大神何恺明之手，它的基本思想是正向传播时，激活值的方差保持不变；反向传播时，关于状态值的梯度的方差保持不变。在tf.keras中也有两种：

• 正态化的he初始化

He 正态分布初始化是以 0 为中心，标准差为 stddev = sqrt(2 / fan_in) 的截断正态分布中抽取样本， 其中 fan_in是输入神经元的个数，在tf.keras中的实现方法为：

# 导入工具包
import tensorflow as tf
# 进行实例化
initializer = tf.keras.initializers.he_normal()
# 采样得到权重值
values = initializer(shape=(9, 1))
# 打印结果
print(values)
12345678

输出结果为：

tf.Tensor(
[[-0.1488019 ]
 [-0.12102155]
 [-0.0163257 ]
 [-0.36920077]
 [-0.89464396]
 [-0.28749225]
 [-0.5467023 ]
 [ 0.27031776]
 [-0.1831588 ]], shape=(9, 1), dtype=float32)

• 标准化的he初始化

He 均匀方差缩放初始化器。它从 [-limit，limit] 中的均匀分布中抽取样本， 其中 limit 是 sqrt(6 / fan_in)， 其中 fan_in 输入神经元的个数。实现为：

# 导入工具包
import tensorflow as tf
# 进行实例化
initializer = tf.keras.initializers.he_uniform()
# 采样得到权重值
values = initializer(shape=(9, 1))
# 打印结果
print(values)

输出结果为：

tf.Tensor(
[[ 0.80033934]
 [-0.18773115]
 [ 0.6726284 ]
 [-0.23672342]
 [-0.6323329 ]
 [ 0.6048162 ]
 [ 0.1637358 ]
 [ 0.60797024]
 [-0.46316862]], shape=(9, 1), dtype=float32)