基于离散Markov模型的Web用户行为预测算法的研究

Posted 2022-08-02 fpga和matlab

目录

一、理论基础

二、案例背景

1.问题描述

2.思路流程

三、部分MATLAB程序

四、仿真结论分析

五、算法相关应用

六、参考文献

---

一、理论基础

        对于 Kth -Markov 模型，常见的建模算法依次扫描每条会话 记录，提取所有长度为 K 的子序列（也称其为状态），同时记录 子序列的下一转移结点，累计发生该转移的计数值。通常采用 矩阵表示。最后，通过计算，将计数值转换为转移概率，形成转 移概率矩阵。预测算法执行时，首先查找与当前用户访问序列 的 K 个后缀相匹配的状态，该状态对应的具有最大转移概率的 转移页面即为预测值。

     根据序列，通过MATLAB编程（func_transition_matrix.m）得到其概率转移矩阵：

然后，做如下的假设：

　  假设所有用户在Web上的浏览过程是一个特殊的随机过程，离散Markov模型。即设离散随机变量的值域为Web空间中的所有网页构成的集合，则一个用户在Web中的浏览过程就构成一个随机变量的取值序列，并且该序列满足Markov性。

　　一个离散的Markov预测模型可以被描述成三元组<S，A，B>，S代表状态空间；A是转换矩阵，表示从一个状态转换到另一个状态的概率；B是S中状态的初始概率分布。其中S是一个离散随机变量，值域为x1，x2,…xn，其中每个xi对应一个网页，称为模型的一个状态。

　　由于，我们要做的是一阶段的Markov预测模型，而该模型是一个典型的无后效性随机过程，也就是说模型在时刻t的状态只与它的前一个时刻t-1的状态条件相关，与以前的状态独立。

那么此时，可以得到t时刻，用户可能存在的状态：

 

 

 

 根据上面的过程，推出First Order Markov Model的基本数学模型。

二、案例背景

1.问题描述

       Web 用户访问互联网，绝大部分情况下是以超级链接为导 航，实现页面间的跳转。如果可以预测用户的行为方向，智能地 选择、提供用户感兴趣的信息，则可以有效地提高 Web 用户使 用互联网的效率。相关的研究成果可以用来解决很多问题，如 在线推荐，减少网络延时，改善网站结构，等等。 建立模型进行 Web 用户行为预测需要权衡模型复杂度和 准确率。

      Markov 模型以其大的信息保留量，从而保证了其预测 准确的特点而成为这方面研究的一个典型模型。但是该模型的 指数级复杂度严重影响了实际的应用。本文以 Markov 模型和 有向图为基础，提出了一种新的预测模型，使其准确度等价于 Markov 模型，但综合复杂度较低，并具有较好的参数调整灵 活性。    

       考虑这样一个web页面请求预测问题，目的就是加速网络服务系统。话句话讲，通过了解哪个页面用户可能要求,可以使用缓存机制。这个练习中，我调查了一阶马尔科夫序列模型，然后将它和随机序列模型在页面预测问题上进行对比，使用真实世界的数据。此外，这个技术在实际中是非常有应用价值的。

2.思路流程

       这里，我们对web用户的行为，定义为如下几种类型：

      包括了17个网页分类，他们分别是：1='frontpg', 2='news', 3='tech', 4='local', 5='opinion', 6='onair', 7='misc', 8='weather', 9='msnnews', 10='health', 11='living', 12='business', 13='msnsport', 14='sports', 15='summary', 16='bbs' and 17='travel'.

       然后通过这些训练样本数据，估计一阶马尔科夫模型的参数，从这个训练数据中。然后使用估计得到的模型区预测后面的NEXT值。然后将测试得到的值和真实值进行对比。然后使用一个衡量指标来说明预测效果。然后自己去找这种衡量指标，然后使用这个指标。

三、部分MATLAB程序

我们在matlab2013b中，编写如下程序，马尔科夫训练过程：

M = zeros(length(train_seq),1);
for m = 1:length(train_seq)
    %transition matrix
    Pm = func_transition_matrix(train_seqm,Nums); 
    %calculate H
    Hm = func_H_vector(train_seqm,Nums); 
    %calculate Next
    [V,I]= max(Hm(end,:) * Pm);
    M(m) = I;
end  

转移矩阵：

function P = func_transition_matrix(data,N); 
Tmp  = data;
T1   = unique(Tmp);

T1Len= inf*ones(N,1);
P    = zeros(N,N);

for i = 1:length(T1)
    T1Len(T1(i)) = length(find(Tmp(1:end-1)==T1(i)));
end
 
for m = 1:length(Tmp) - 1;
    P(Tmp(m),Tmp(m+1)) = P(Tmp(m),Tmp(m+1)) + 1 / T1Len(Tmp(m));    
end

对比算法随机序列：

function [Seq,Ps] = func_random_whole(data,Nums);

%Seq
%ML p
P2    = tabulate(data); 
%predection
[V,I] = max(P2(:,end));
Seq   = [data I];

%Seq probability
tmps    = tabulate(Seq);
Pss     = tmps(:,3)/100;
Ind     = tmps(:,2);

Ps = 1;
for i = 1:length(Pss)
    Ps = Ps*Pss(i)^Ind(i);
end

四、仿真结论分析

        对预测结果的评价，我们使用的指标为：即分析不同连接深度下，预测的正确率。 仿真结果如下：

       这里，仿真误差图的含义为，对于每个用户点击深度，即当用户点击N次，随后通过First Order Markov Model和Random sequence model预测得到的第N+1次的web浏览情况，那么对于之前的历史数据N，不同长度下，对应不同的预测错误概率。

然后使用随机序列进行重复试验作为对比：

将两种方法的结论进行对比：

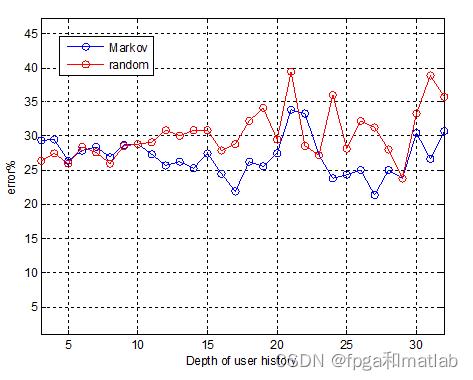
 从上面的仿真对比可知，采用离散Markov预测模型，其预测效果优于采用随机序列的预测方法。 

这里，通过均值，方差以及MSE三个指标对两种模型进行误差分析：

Table1 The comparison of Markov and Random

	Markov	Random
E	0.2010	0.2587
D	0.1608	0.1695
MSE	0.066	0.0953

       通过上面的仿真结果可知，采用First Order Markov Model模型预测得到的web浏览情况，其错误概率大概在25%~30%左右。而使用Random sequence model模型预测得到的web浏览情况，其错误概率大概在30%~35%左右。并且，两种模型，随着深度的增加，错误概率变大。

      此外，通过计算预测误差的期望和方差可以看到，First Order Markov Model的值均小于Random sequence model预测得到的值。

      最后，再次通过对MSE值，通过仿真，First Order Markov Model的值为0.0660，Random sequence model的值为0.0953。

      通过上述的仿真波形以及数据分析表明，采用First Order Markov Model的预测精度大于Random sequence model的预测精度。

五、算法相关应用

       基于离散Markov模型的Web用户行为预测算法，通过增加Markov模型阶数，可以实现更为复杂的互联网用户行为预测。从而将该算法应用到用户喜好推荐，异常网页浏览行为判决等相关领域。相对于深度学习的预测方法，通过一阶马尔科夫判决方法，其依赖样本的程度较小，可以在训练样本较少的情况下，完成对web用户的行为预测。

六、参考文献

[1]张玉成, 徐大纹, 王筱娟. 基于加权马尔可夫链的主动用户行为预测模型[J]. 计算机工程与设计, 2011, 32(10):5.

[2]李爱春, 滕少华. Web挖掘在网络广告点击欺诈检测中的应用[J]. 计算机工程与设计, 2012, 33(3):6.A5-10