论文|万物皆可Vector之Word2vec:2个模型2个优化及实战使用
Posted 搜索与推荐Wiki
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文|万物皆可Vector之Word2vec:2个模型2个优化及实战使用相关的知识,希望对你有一定的参考价值。
万物皆可Embedding系列会结合论文和实践经验进行介绍,前期主要集中在论文中,后期会加入实践经验和案例,目前已更新:
- 万物皆可Vector之语言模型:从N-Gram到NNLM、RNNLM
- 万物皆可Vector之Word2vec:2个模型、2个优化及实战使用
- Item2vec中值得细细品味的8个经典tricks和thinks
后续会持续更新Embedding相关的文章,欢迎持续关注「搜索与推荐Wiki」
2.1、背景介绍
word2vec 是Google 2013年提出的用于计算词向量的工具,在论文Efficient Estimation of Word Representations in Vector Space中,作者提出了Word2vec计算工具,并通过对比NNLM、RNNLM语言模型验证了word2vec的有效性。
word2vec工具中包含两种模型:CBOW和skip-gram。论文中介绍的比较简单,如下图所示,CBOW是通过上下文的词预测中心词,Skip-gram则是通过输入词预测上下文的词。

2.2、CBOW 和 Skip-gram
原论文对这两种模型的介绍比较粗略,在论文《word2vec Parameter Learning Explained》中进行了详细的解释和说明,接下来我们详细看下CBOW和Skip-gram。
a)CBOW
One-word context
首先看一下只有一个上下文词的情况
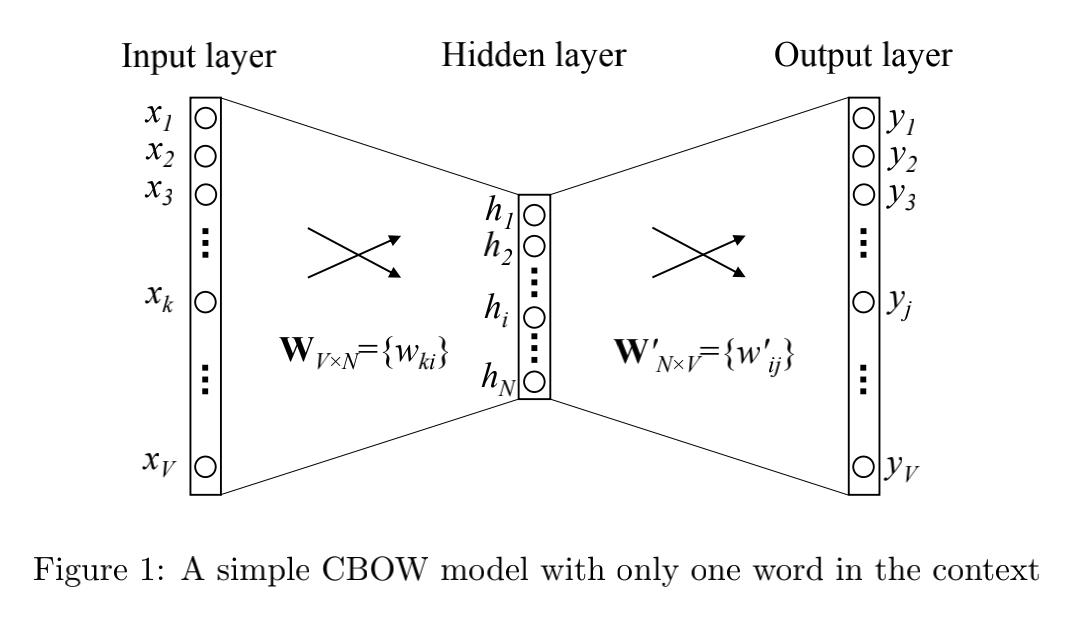
其中单词的总个数为 V V V,隐藏层的神经元个数为 N N N,输入层到隐藏层的权重矩阵为 W V ∗ N W_V*N WV∗N,隐藏层到输出层的权重矩阵为 W N ∗ V ′ W'_N*V WN∗V′。
输入层是单词的One-hot编码。从输入层到隐藏层:
h
=
W
T
x
:
=
v
w
I
T
h = W^T x := v^T_w_I
h=WTx:=vwIT
v
w
I
v_w_I
vwI 表示的就是输入单词
w
I
w_I
wI的向量表示(注意和输入层
x
x
x进行区分,输入向量即
W
W
W中的向量表示,输出向量即
W
′
W'
W′中的向量表示),其维度为
[
N
,
1
]
[N, 1]
[N,1],转置后维度变成了
[
1
,
N
]
[1,N]
[1,N],用来表示向量的输入表述,要注意这里不是
[
1
,
N
]
[1,N]
[1,N],否则容易在往下的第二个公式中相乘时维度搞混,符号
:
=
:=
:=表示的定义为。
从隐藏层到输入层:
u
j
=
(
v
w
j
′
)
T
h
u_j = (v'_w_j)^T h
uj=(vwj′)Th
其中
v
w
j
′
v'_w_j
vwj′ 表示的是矩阵
W
′
W'
W′的第
j
j
j 列,其维度为
[
N
,
1
]
[N,1]
[N,1],计算出来的
u
j
u_j
uj为一个具体的值,表示的是第
j
j
j个输入的词在输出层第
j
j
j个位置对应的值。
最后使用
s
o
f
t
m
a
x
softmax
softmax进行归一化处理(因为输出层是固定的
V
V
V个单词,所以可以看作是多分类,因此使用
s
o
f
t
m
a
x
softmax
softmax进行归一化),得到输入单词
w
I
w_I
wI所属词库中每个单词的概率:
p
(
w
j
∣
w
I
)
=
y
j
=
e
x
p
(
u
j
)
∑
j
′
=
1
V
e
x
p
(
u
j
′
)
p(w_j | w_I) = y_j = \\fracexp(u_j) \\sum_j'=1^Vexp(u_j')
p(wj∣wI)=yj=∑j′=1Vexp(uj′)exp(uj)
其中
y
j
y_j
yj 表示的是输出层的第
j
j
j个神经元的值。
联合上面三个公式可得:
p
(
w
j
∣
w
I
)
=
e
x
p
(
(
v
w
j
′
)
T
∗
v
w
I
T
)
∑
j
′
=
1
V
e
x
p
(
(
v
w
j
′
′
)
T
∗
v
w
I
T
)
p(w_j | w_I) = \\frac exp((v'_w_j)^T * v^T_w_I) \\sum_j'=1^Vexp((v'_w_j')^T * v^T_w_I)
p(wj∣wI)=∑j′=1Vexp((vwj′′)T∗vwIT)exp((vwj′)T∗vwIT)
其中 v w v_w vw可以理解为单词的输入向量表示, v w ′ v_w' vw′为单词的输出向量表示。
此种情况下的损失函数为:
m
a
x
p
(
w
O
∣
w
I
)
=
m
a
x
y
j
∗
=
m
a
x
l
o
g
y
j
∗
=
u
j
∗
−
l
o
g
∑
j
′
=
1
V
e
x
p
(
u
j
′
)
:
=
−
E
max \\, \\, p(w_O|w_I) = max \\, y_j* \\\\ = max \\, log \\, y_j* \\\\ = u_j* - log \\sum_j'=1^V exp(u_j') \\\\ := -E
maxp(wO∣wI)=maxyj∗=maxlogyj∗=uj∗论文|万物皆可Vector之语言模型:从N-Gram到NNLMRNNLM