论文｜DeepWalk的算法原理代码实现和应用说明

Posted 2021-05-19 Thinkgamer_

万物皆可Embedding系列会结合论文和实践经验进行介绍，前期主要集中在论文中，后期会加入实践经验和案例，目前已更新：

• 万物皆可Vector之语言模型：从N-Gram到NNLM、RNNLM
• 万物皆可Vector之Word2vec：2个模型、2个优化及实战使用
• Item2vec中值得细细品味的8个经典tricks和thinks
• Sentence2Vec & GloVe 算法原理、推导与实现
• Doc2vec的算法原理、代码实现及应用启发
• DeepWalk的算法原理、代码实现和应用说明

后续会持续更新Embedding相关的文章，欢迎持续关注「搜索与推荐Wiki」，戳文末「阅读原文」触达更多有关「推荐系统」笔记！

1、概述

DeepWalk是2014年提出的一种Graph Embedding 算法，是首次将NLP w2v和graph embedding进行结合，关于词嵌入（embedding）是使用一个向量表示文本中的某一个词，在训练的时候w2v分为两种，一种是用一个词预测上下文（Skip-gram），另一种则是用上下文预测一个词（CBOW），关于w2v的详解介绍可以参考《论文笔记》前几篇的内容。

Deepwalk在这里使用网络中的节点代表文本中的每一个词，用截断随机游走的路径代表一个句子，然后套用Skip-gram算法进行嵌入表示的学习。

2、算法过程

论文中提到优秀的社群表示需要有下面的特征：适应性，社群内相似性，低维和连续性。

• 适应性：网络表示必须能适应网络的变化。网络是一个动态的图，不断地会有新的节点和边添加进来，网络表示需要适应网络的正常演化
• 社群内相似性：属于同一个社区的节点有着类似的表示，网络中往往会出现一些特征相似的点构成的团状结构，这些节点表示成向量后必须相似
• 低维：代表每个顶点的向量维数不能过高，过高会有过拟合的风险，对网络中有缺失数据的情况处理能力较差
• 连续性：低维的向量应该是连续的

Deepwalk算法的核心步骤分为两步：

• 随机游走采样节点序列
• 使用Skip-gram model学习表达向量

整个算法的流程为：

其中第2步是构建Hierarchical Softmax，第3步对每个节点做$\gamma$次随机游走，第4步打乱网络中的节点，第5步以每个节点为根节点生成长度为t的随机游走，第7步根据生成的随机游走使用Skip-gram模型利用梯度的方法对参数进行更新。

2.1 Random Walks

随机游走算法，其实在文中更精确的是截断式随机游走，也就是长度固定的随机游走。随机游走这一步其实更像是为网络标识的学习来收集训练数据，或者说是进行采样工作。算法的思想其实是很简单的，主要就是对网络中的每个节点作为root随机的找下一个节点进行游走，然后长度为固定好的。然后每个节点可以有好几个Walker，这些都是可以自己设定的参数。

这个算法使其具有了可以高度并行化和适应性的特点，因为每个节点的随机游走都可以并行的同时开始，同时对于网络的部分更新我们也可以只在整个网络更新的小部分进行随机游走。

2.2 Skip-gram

随机游走后需要进行的就是skip-gram算法了，使用random walk生成了大量的训练数据。后面就采用训练word2vec相同的思路来训练就可以了。w2v有两种训练方式，这里使用的是skipgram的方式也就是用一个词来预测它的上下文，这里忽略的词序的信息以及和当前词的距离。

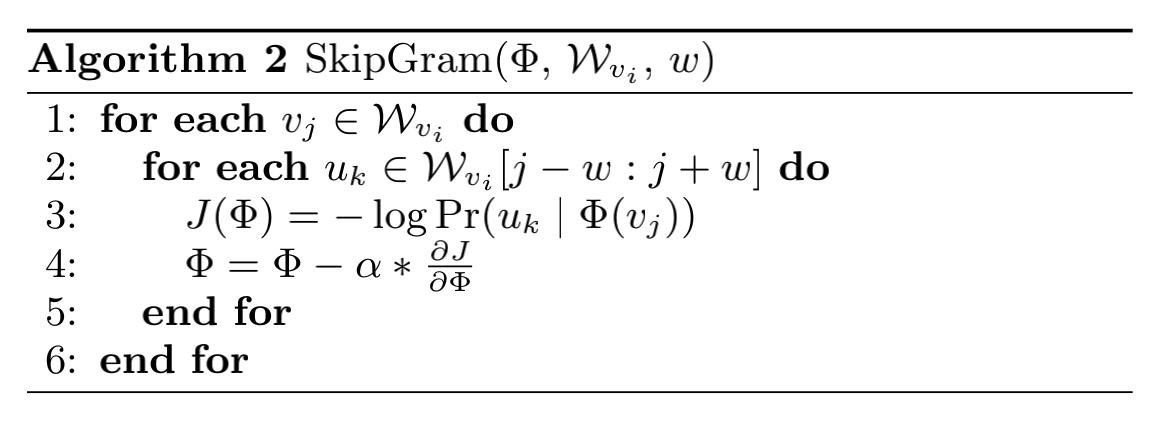
2.3 Hierarchical Softmax

这个也是w2v中的技术，就是为了解决标签过多在使用softmax时带来的计算量大的问题。这里需要我们生成一个二叉树，叶子节点就是每个类别。假设一共有V个类别，原始softmax的计算量就是$O(V)$，使用二叉树后，从根节点到叶子节点的距离就变成了$O(logV)$。

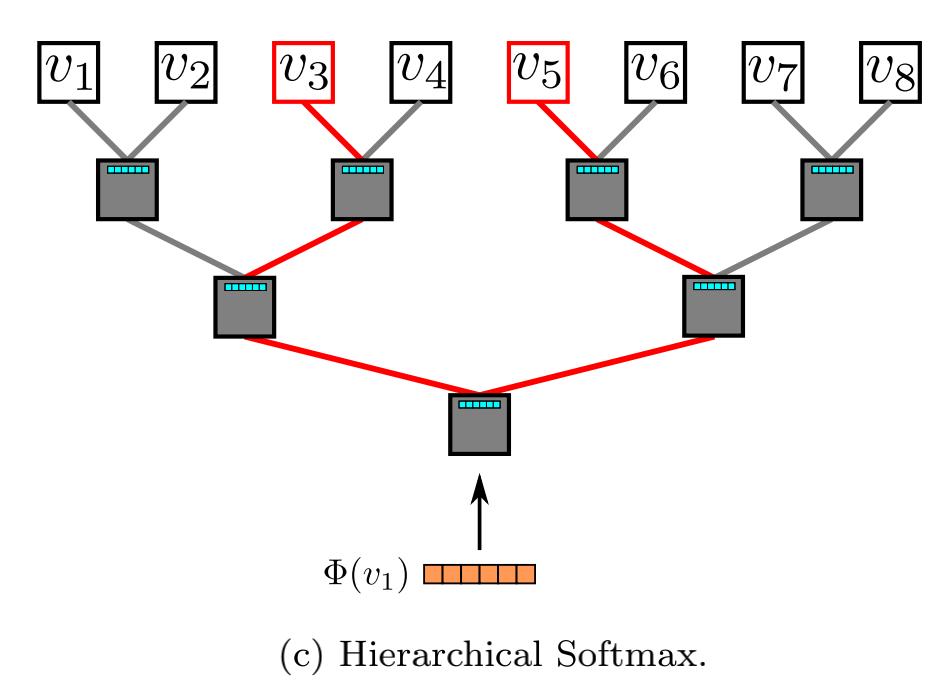
2.4 Power-law Distribution

论文中使用的是w2v中的skip-gram模型进行embedding的学习。那么为什么deepwalk随机游走出来的序列可以套用skip-gram呢？

文中提到网络中随机游走的分布规律与NLP中句子序列在语料库中出现的规律有着类似的幂律分布特征。那么既然网络的特性与自然语言处理中的特性十分类似，那么就可以将NLP中词向量的模型用在网络表示中。

3、实验

论文中采用的实验参数为：

• $\gamma$ =80（每个节点被采样的次数）
• $w$ = 10 （滑动窗口）
• $d$ = 128 （向量的维度）
• $t$ = 40 （游走的节点长度）

实验指标：Macro-F1 and Micro-F1 表示的含义是什么？

F1的核心思想在于，在尽可能的提高Precision和Recall的同时，也希望两者之间的差异尽可能小。F1-score适用于二分类问题，对于多分类问题，将二分类的F1-score推广，有Micro-F1和Macro-F1两种度量。

• Micro-F1：统计各个类别的TP、FP、FN、TN，加和构成新的TP、FP、FN、TN，然后计算Micro-Precision和Micro-Recall，得到Micro-F1
• Macro-F1：统计各个类别的TP、FP、FN、TN，分别计算各自的Precision和Recall，得到各自的F1值，然后取平均值得到Macro-F1

从上面二者计算方式上可以看出，Macro-F1平等地看待各个类别，它的值会受到稀有类别的影响；而Micro-F1则更容易受到常见类别的影响。

关于F1-Scorede计算过程可以参考：

• F1-score与Macro-F1、Micro-F1计算与理解

• Macro-F1 Score与Micro-F1 Score

4、代码实现

deepwalk的核心类实现为：

"""
    Author  : Thinkgamer
    File    : DeepWalk.py
    Desc    : DeepWalk Model
"""
import numpy as np
from gensim.models import Word2Vec

class DeepWalk:

	def __init__(self, graph, walk_numbers=10, walk_deep=20, embeding_size=128, window_size=5, workers=3, iters=5, min_count=0, sg=1, hs=1, negative=1, seed=128, compute_loss=False, is_save_sentence=False, save_sentence_path=None, **kwargs):
		"""
			DeepWalk Model 函数类初始化
		:param graph: 创建的 networdx 对象
		:param walk_numbers: 每个节点创建多少个序列
		:param walk_deep: 遍历的深度
		:param embeding_size: 生成的embedding 大小「word2vec参数」
		:param window_size: 窗口大小「word2vec参数」
		:param workers: 采用多少个线程生成embedding 「word2vec参数」
		:param iters: 迭代次数「word2vec参数」
		:param min_count: 过滤词频低于改值的item「word2vec参数」
		:param sg: 1 表示 Skip-gram 0 表示 CBOW「word2vec参数」
		:param hs: 1 表示 hierarchical softmax  0 且 negative 参数不为0 的话 negative sampling 会被启用「word2vec参数」
		:param negative: 0 表示不采用，1 表示采用，建议值在 5-20 表示噪音词的个数「word2vec参数」
		:param seed: 随机初始化的种子「word2vec参数」
		:param compute_loss: 是否计算loss「word2vec参数」
		:param is_save_sentence: 是否保存序列数据
		:param save_sentence_path: 保存序列数据的路径
		:param kwargs:
		"""
		self.walk_numbers = walk_numbers
		self.walk_deep = walk_deep

		self.embedding_size = embeding_size
		self.window_size = window_size
		self.workers = workers
		self.iter = iters
		self.min_count = min_count
		self.sg = sg
		self.hs = hs
		self.negative = negative
		self.seed = seed
		self.compute_loss = compute_loss

		self.graph = graph
		self.w2v_model = None
		self.is_save_sentence = is_save_sentence
		self.save_sentence_path = save_sentence_path
		self.sentences = self.gen_sentences()

	def gen_sentences(self):
		sentences = list()
		i = 0
		for node in self.graph.nodes:
			i += 1
			print("开始从节点 i={}: {} 开始生成随机游走序列！".format(i, node))
			_corpus = list()
			for walk_number in range(self.walk_numbers):
				sentence = [node]
				current_node = node
				deep = 0
				while deep < self.walk_deep:
					deep += 1
					node_nbr_list = list()
					node_weight_list = list()
					if self.graph[current_node].items().__len__() == 0:
						continue
					for nbr, weight_dict in self.graph[current_node].items():
						node_nbr_list.append(nbr)
						node_weight_list.append(weight_dict["weight"])
					node_weight_norm_list = [float(_weight) / sum(node_weight_list) for _weight in node_weight_list]
					new_current_node = np.random.choice(node_nbr_list, p=node_weight_norm_list)
					sentence.append(new_current_node)
					current_node = new_current_node
			sentences.append(sentence)
		if self.is_save_sentence:
			fw = open(self.save_sentence_path, "w")
			for sentence in sentences:
				fw.write(",".join(sentence) + "\\n")
			fw.close()
		return sentences

	def train(self, **kwargs):
		kwargs["sentences"] = self.sentences
		kwargs["iter"] = self.iter
		kwargs["size"] = self.embedding_size
		kwargs["window"] = self.window_size
		kwargs["min_count"] = self.min_count
		kwargs["workers"] = self.workers
		kwargs["sg"] = self.sg
		kwargs["hs"] = self.hs
		kwargs["negative"] = self.negative
		kwargs["seed"] = self.seed
		kwargs["compute_loss"] = self.compute_loss
		model = Word2Vec(**kwargs)
		print("DeepWalk Embedding Done!")

		self.w2v_model = model
		return model

	def embedding(self, word):
		return self.w2v_model.wv[word]

	def embeddings(self):
		embedding_dict = dict()
		for node in self.graph.nodes:
			embedding_dict[node] = self.embedding(node)
		return embedding_dict

	def similarity(self, word1, word2):
		return self.w2v_model.wv.similarity(word1, word2)

	def most_similar(self, word, topn=200):
		return self.w2v_model.wv.most_similar(word, topn=topn)

	def save_embedding(self, path):
		fw = open(path, "w")
		for node in self.graph.nodes:
			fw.write(node + "\\t" + ",".join(map(str, list(self.embedding(node)))) + "\\n")
		fw.close()
		print("embedding save to: {} done!".format(path))

	def save_node_sim_nodes(self, path, topn=200):
		fw = open(path, "w")
		for node in self.graph.nodes:
			_list = list()
			for sim_node in self.most_similar(node, topn=topn):
				_list.append(sim_node[0] + ":" + format(sim_node[1], ".4f"))
			fw.write(node + "\\t" + ",".join(_list) + "\\n")
		fw.close()
		print("nodes sim nodes save to: {} done!".format(path))

5、应用

DeepWalk算法被广泛应用在推荐系统中，如上面的代码实现案例中，我们可以利用deepwalk算法产出item、或者user的向量，继而进行向量召回、聚类等工作。

---

【技术服务】详情点击查看： https://mp.weixin.qq.com/s/PtX9ukKRBmazAWARprGIAg

---

扫一扫关注「搜索与推荐Wiki」！号主「专注于搜索和推荐系统，以系列分享为主，持续打造精品内容！」