不懂点儿统计学,《星球大战》白看了
Posted turingbooks
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了不懂点儿统计学,《星球大战》白看了相关的知识,希望对你有一定的参考价值。
很久很久以前,在一个遥远的星系……
我们的英雄汉·索罗正驾驶着“千年隼”号全速躲避歼星舰和钛战机的追击。
慌乱中,机器人C-3PO提示说,“千年隼”号的超光速推进器坏了。更糟糕的是,飞船还被小行星撞了一下。
这一撞给了汉·索罗灵感。只见他坐进驾驶位,调整状态,将“千年隼”号径直驶入了小行星带。
一向见多识广的C-3PO在他身后连忙提示道:“长官,成功穿过小行星带的概率大约是1比3720!”
“千万别跟我提概率!”汉·索罗回答道。

《星球大战:帝国反击战》剧照
(来源:imdb.com)
如果看过《星球大战:帝国反击战》,那么你一定对以上名场面记忆犹新。在扣人心弦的情节背后,其实隐藏了一个有趣的统计学知识。我们来仔细看看。
一方面,我们都知道拥有主角光环的汉·索罗定能成功穿过小行星带。另一方面,我们也知道C-3PO的数据很合理,因为的确没有一架钛战机成功穿过小行星带。
汉·索罗认为自己成功穿过小行星带的概率 = 100%
C-3PO计算的成功穿过小行星带的概率 = 1 / 3720 = 0.027%
既然双方都有道理,那为什么两个概率的差距如此之大呢?
似然:C-3PO的推理方式
C-3PO并没有错,它只是忘了重要信息——汉·索罗是高手,超级厉害!
C-3PO并没有胡编乱造,它精通600多万种通信方式,这需要大量的数据支持。所以我们可以基本确定,“1比3720”的说法是有数据支撑的。
我们根据C-3PO给出的数据,使用β分布来确定成功概率。之所以使用β分布,是因为在给定成功和失败比例的情况下,它能正确地模拟一个事件的各种可能概率。
β分布的参数是α(观察到的成功次数)和β(观察到的失败次数):
Beta(α,β)
这个分布告诉我们,根据目前掌握的数据,C-3PO认为成功穿过小行星带的概率最有可能是多少。
为了弄清C-3PO的推理方式,这里做些合理的假设。我们假设C-3PO的记录显示仅有两个人成功穿越过小行星带,而其他的7440人则在剧烈的爆炸中结束了小行星带之旅。
下图展示了β分布,即Beta(2, 7440)。
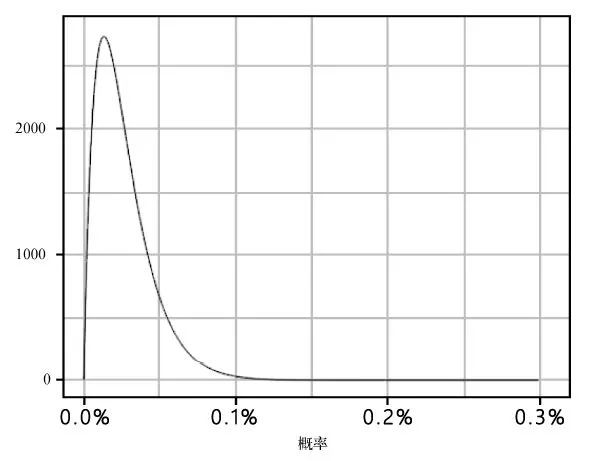
成功希望如此渺茫!怪不得连汉·索罗自己都认为冲进小行星带很危险,所以他说道:“他们一定是疯了才会跟着我们。”
先验:汉·索罗的厉害之处
C-3PO的分析存在的问题是,它掌握的数据是关于所有飞行员的,但汉·索罗并非普通的飞行员。
我们的先验信念是,汉·索罗一定能成功穿过小行星带,因为他有主角光环。
先验信念的概率往往颇具争议性。很多人觉得“编造”一个先验概率很不客观。但你要知道,否定先验概率更荒谬。
我们有很多理由相信汉·索罗会活下来,却没有数据来支撑这个信念。先来看看他的厉害程度的上界。(是的,应该有一个上界,不是吗?如果我们相信他绝对不会死,那么这部电影就老套且无聊了。)
我们有很强的信念认为汉·索罗会成功穿过小行星带。这里再次做出合理的假设。假定我们相信他会活下来的信念是20000比1。
下图显示了我们相信汉·索罗会活下来的先验概率分布,即Beta(20000, 1)。
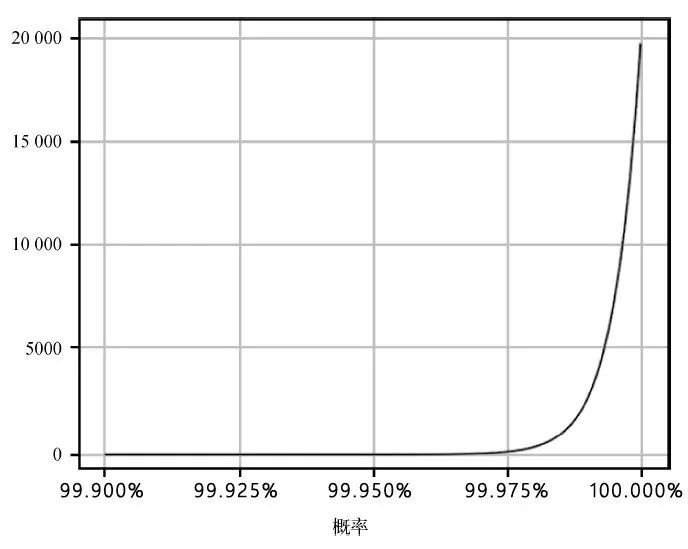
后验:编剧如何制造悬念
我们已经确定了C-3PO的信念(似然),也建立了对汉·索罗的信念模型(先验概率分布)。接下来需要一种方法将二者结合起来,形成最终的后验信念。
我们像下面这样组合上述两个β分布,得到后验概率分布。
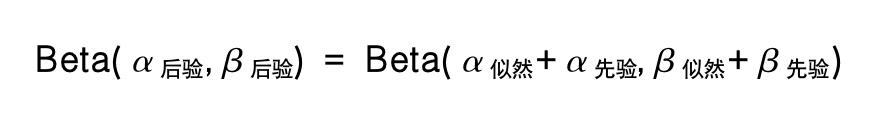
代入具体的值,有:
Beta(2+20000,7440+1) = Beta(20002,7441)
从下图可以直观地看到后验概率分布。
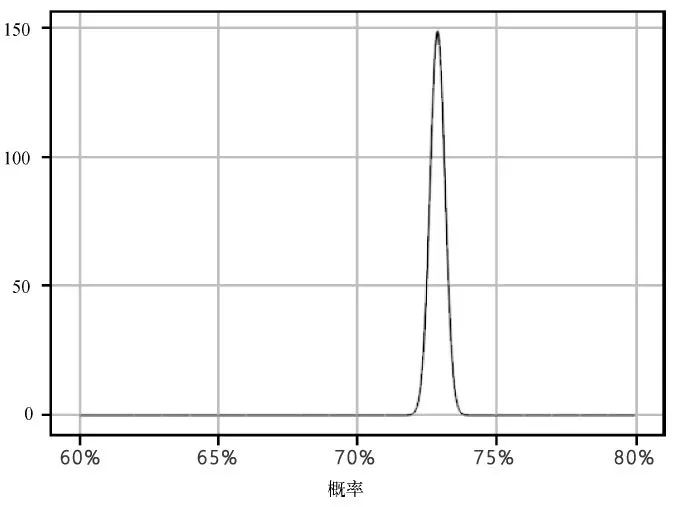
可以看到,通过将C-3PO的信念与“汉·索罗很厉害”的信念结合起来,我们发现他成功活下来的概率大约是73%。
这意味着我们仍然认为汉·索罗有很大的机会成功,但我们还是会为他担心。
结语
通过这个例子,我们了解到似然、先验和后验的关系。实际上,这三者正是贝叶斯定理的三要素。
C-3PO的数据提供了与我们对汉·索罗能力的认知不符的似然,但我们并没有直接否定C-3PO的数据,而是将似然与我们的先验信念结合起来,形成调整后的最终信念(后验)。
在电影中,这种不确定性对营造紧张氛围至关重要。
在现实生活中,掌握了贝叶斯定理的基本逻辑,你也能用它来分析你所遇到的任何不确定情形。
新 书 推 荐

以上是关于不懂点儿统计学,《星球大战》白看了的主要内容,如果未能解决你的问题,请参考以下文章
看完了这篇实时数仓建设,才发现以前的都白看了(内有美团案例)