DL：RBM学习算法——Gibbs采样变分方法对比散度模拟退火

Posted 2022-06-17 happy_XYY

RBM学习算法——Gibbs采样、变分方法、对比散度、模拟退火

在学习Hinton的stack autoencoder算法（论文 Reducing the Dimensionality of Data with Neural Networks）之前需要了解什么是RBM，现在就我学习的情况，查找的资料（大部分来自博客、论文），简单介绍一下RBM。（当然，这里面还有同组实验的同学提供的资料，借用一下。。。）

目录

RBM简介、网络结构

Hopfield 神经网络

RBM能量模型

RBM学习算法——Gibbs采样、变分方法、对比散度、模拟退火

RBM训练算法

RBM评估

当前在对RBM 的研究中，典型的学习方法有Gibbs 采样(Gibbs sampling)算法，变分近似方法(variational approach)，对比散度(contrastive divergence,CD)算法，模拟退火(simulate annealing) 算法等。下面对这些方法进行对比。

1、Gibbs采样算法

（1）简介

Gibbs 采样(Gibbs sampling)算法是一种基于马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)策略的采样方法。wikipedia称gibbs抽样为

　　

In statistics and in statistical physics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for obtaining a sequence of observations which are approximately from a specified multivariate probability distribution (i.e. from the joint probability distribution of two or more random variables), when direct sampling is difficult.

意思是，在统计学和统计物理学中，gibbs抽样是马尔可夫链蒙特卡尔理论（MCMC）中用来获取一系列近似等于指定多维概率分布（比如2个或者多个随即变量的联合概率分布）观察样本的算法。

MCMC是用于构建 Markov chain随机概率分布的抽样的一类算法。MCMC有很多算法，其中比较流行的是Metropolis-Hastings Algorithm，Gibbs Sampling是Metropolis-Hastings Algorithm的一种特殊情况。

Markov chain 是一组事件的集合，在这个集合中，事件是一个接一个发生的，并且下一个事件的发生，只由当前发生的事件决定。用数学符号表示就是：

　　　　 A= a1,a2 … ai, ai+1,… at 

　　　　P(ai+1| a1,a2,…ai) = P(ai+1| ai)

　　这里的ai不一定是一个数字，它有可能是一个向量，或者一个矩阵，例如我们比较感兴趣的问题里ai= （g, u, b）这里g表示基因的效应，u表示环境效应，b表示固定效应，假设我们研究的一个群体，g，u，b的联合分布用π（a）表示。事实上，我们研究QTL（QTL是quantitative trait locus的缩写，中文可以翻译成数量性状座位或者数量性状基因座，它指的是控制数量性状的基因在基因组中的位置。对QTL的定位必须使用遗传标记，人们通过寻找遗传标记和感兴趣的数量性状之间的联系，将一个或多个QTL定位到位于同一染色体的遗传标记旁，换句话说，标记和QTL是连锁的。），就 是要找到π（a），但是有时候π（a）并不是那么好找的，特别是我们要估计的a的参数的个数多于研究的个体数的时候。用一般的least square往往效果不是那么好。

解决方案：

　　用一种叫Markov chain Monte Carlo (MCMC)的方法产生Markov chain，产生Markov chaina1,a2 … ai, ai+1,… at 具有如下性质：

当t 很大时，比如10000，那么at ~ π（a），这样的话如果我们产生一个markov chaina1,a2 … ai, ai+1,… a10000，那么我们取后面9000个样本的平均 a_hat = (g_hat,u_hat,b_hat) = ∑ai / 9000 (i=1001,1002, … 10000)这里g_hat, u_hat, b_hat 就是基因效应，环境效应，以及固定效应的估计值

MCMC算法的关键是两个函数：

1）    q（ai, ai+1），这个函数决定怎么基于ai得到ai+1

2）    α（ai, ai+1），这个函数决定得到的ai+1是否保留

目的是使得at的分布收敛于π（a）

（2）Gibbs Sampling的算法

一般来说我们通常不知道π（a），但我们可以得到p（g | u , b）,p(u | g , b), p ( b | g, u )即三个变量的posterior distribution

Step1: 给g, u, b 赋初始值：（g0,u0,b0）

Step2: 利用p (g | u0, b0) 产生g1

Step3: 利用p (u | g1, b0) 产生u1

Step4: 利用p (b | g1, u1) 产生b1

Step5: 重复step2~step5 这样我们就可以得到一个markov chain a1,a2 … ai, ai+1,… at

这里的q（ai, ai+1）= p（g | u , b）* p(u | g , b)* p ( b | g, u )

 

（3）综述

给定一个N 维的随机向量X=(X1,X2,…,XN)，若直接求取X的联合分布P(X1,X2,…,XN)非常困难，但如果可以在给定其他分量时，求得第k 个分量的条件分布P(Xk|Xk-)，其中Xk-=(X1,X2,…,Xk-1,Xk+1,…,XN)指代排除Xk的其他N-1 维的随机向量，则可以从X 的一个任意状态[x1(0),x2(0),…,xk(0)]开始，利用条件分布，对各分量依次迭代采样。随着采样次数增加，随机变量[x1(n),x2(n),…,xk(n)]将会以几何级数的速度收敛于联合分布P(X1,X2,…,XN)。在训练RBM 的迭代过程中，可以设置一个收敛到模型分布的马尔可夫链，将其运行到平衡状态时，用马尔可夫链近似期望值Epmodel<·> 。

使用Gibbs 采样算法具有通用性好的优点，但是由于每次迭代中都需要马尔可夫链达到极限分布，而Gibbs 采样收敛度缓慢，需要很长的时间，因此也限制了其应用。

2、变分方法

变分方法(variational approach)的基本思想是通过变分变换将概率推理问题转换为一个变分优化问题。对于比较困难的概率推理问题，对应的变分优化问题通常也缺乏有效的精确解法，但此时可以对变分优化问题进行适当的松弛，借助于迭代的方法，获得高效的近似解。在变分学习中，对每个训练样本可见单元向量v，用近似后验分布q(h|v,μ)替换隐藏单元向量上的真实后验分布p(h|v,θ)，则RBM 模型的对数似然函数有下面形式的变分下界：

 

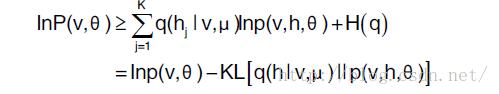
其中H(·)为熵函数。

使用变分法的优势在于，它能够在实现最大化样本对数似然函数的同时，最小化近似后验分布与真实后验分布之间的K-L 距离。若采用朴素平均场方法，选择完全可因式分解化的分布来近似真实后验分布

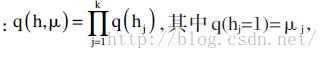
训练样本的对数似然函数的下界有如下的形式：

 

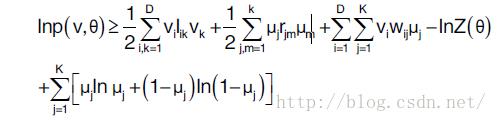
采用交替优化的方式，首先固定参数θ，最大化上式学习变分参数μ，得到不平均场不动点方程：

 

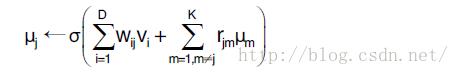
接下来，再给定变分参数μ，采用Gibbs 采样法与模拟退火方法等其他方法更新模型参数θ。在实际使用中，使用变分方法能够很好地估计数据期望Epdata<·> ，但由于Inp(v,θ)中的负号会改变变分参数，使得近似后验分布与真实后验分布的K-L 距离增大，因此将其用来近似模型期望Epmodel<·> 时不适用。

 

3、对比散度算法

（1）算法

（2）综述

对比散度(contrastive divergence, CD)学习方法由Hinton提出，能够有效地进行RBM 学习，而且能够避免求取对数似然函数梯度的麻烦，因此在基于RBM 构建的深度模型中广泛使用。CD 算法使用估计的概率分布与真实概率分布之间K-L 距离作为度量准则。在近似的概率分布差异度量函数上求解最小化。执行CD 学习算法时，对每个批次的各训练样本运行n步Gibbs 采样，使用得到的样本计算Epmodel<·> 。则连接权重的CD梯度近似为：

 

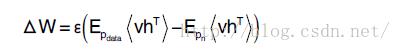
其中pn为n 步Gibbs 采样后获得的概率分布。通常在使用中只需要取n=1 即可以进行有效的学习，因此在使用中较为方便。但CD 算法随着训练过程的进行与参数的增加，马尔可夫链的遍历性将会下降，此时算法对梯度的近似质量也会退化。

 

 

4、模拟退火算法(Simulated Annealing)

（1）简介

模拟退火算法(Simulated Annealing，SA)最早的思想是由N. Metropolis[1]  等人于1953年提出。1983 年,S. Kirkpatrick 等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般 组合优化问题之间的相似性。模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用，诸如VLSI、生产调度、控制工程、机器学习、神经网络、信号处理等领域。

模拟退火算法是通过赋予搜索过程一种时变且最终趋于零的概率突跳性，从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。

（2）SA 原理

模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。根据Metropolis准则，粒子在温度T时趋于平衡的概率为e(-ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变量，k为Boltzmann常数。用固体退火模拟组合优化问题，将内能E模拟为目标函数值f，温度T演化成控制参数t，即得到解组合优化问题的模拟退火算法：由初始解i和控制参数初值t开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步衰减t值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。

（3）SA模型

1模拟退火算法可以分解为解空间、目标函数和初始解三部分。

2模拟退火的基本思想:

(1) 初始化：初始温度T(充分大)，初始解状态S(是算法迭代的起点)，每个T值的迭代次数L

(2) 对k=1，……，L做第(3)至第6步：

(3) 产生新解S′

(4) 计算增量Δt′=C(S′)-C(S)，其中C(S)为评价函数

(5) 若Δt′<0则接受S′作为新的当前解，否则以概率exp(-Δt′/T)接受S′作为新的当前解.

(6) 如果满足终止条件则输出当前解作为最优解，结束程序。

终止条件通常取为连续若干个新解都没有被接受时终止算法。

(7) T逐渐减少，且T->0，然后转第2步。

（4）步骤

模拟退火算法新解的产生和接受可分为如下四个步骤：

第一步是由一个产生函数从当前解产生一个位于解空间的新解；为便于后续的计算和接受，减少算法耗时，通常选择由当前 新解经过简单地变换即可产生新解的方法，如对构成新解的全部或部分元素进行置换、互换等，注意到产生新解的变换方法决定了当前新解的邻域结构，因而对冷却 进度表的选取有一定的影响。

第二步是计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生，所以目标函数差的计算最好按增量计算。事实表明，对大多数应用而言，这是计算目标函数差的最快方法。

第三步是判断新解是否被接受,判断的依据是一个接受准则，最常用的接受准则是Metropolis准则: 若Δt′<0则接受S′作为新的当前解S，否则以概率exp(-Δt′/T)接受S′作为新的当前解S。

第四步是当新解被确定接受时，用新解代替当前解，这只需将当前解中对应于产生新解时的变换部分予以实现，同时修正目标函数值即可。此时，当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时，则在原当前解的基础上继续下一轮试验。

模拟退火算法与初始值无关，算法求得的解与初始解状态S(是算法迭代的起点)无关；模拟退火算法具有渐近收敛性，已在理论上被证明是一种以概率l 收敛于全局最优解的全局优化算法；模拟退火算法具有并行性。

 

（5）综述

模拟退火算法是对Gibbs 采样算法的改进，由于Gibbs 采样收敛速度缓慢，因此模拟退火算法采用有索引温度参数的目标分布

进行采样，其核心思想是模拟多个不同的温度并行运行多个MCMC 链，每个MCMC 链在一个有序序列温度ti上，且t0=1<t1<…<ti<…<tT-1<tT=τ，其中t0=1 为目标分布采样温度，tT=τ为高温。并引入交叉温度状态互换操作，即每个运行步骤中，以交换概率 交换温度ti与t(i+1)上运行的两个相邻链之间的样本。对于Gibbs 分布，有

为逆温度参数。在每个梯度更新中，随机选择的相邻链间状态交换后，所有的MCMC 链执行一步Gibbs 采样。这样高温下的MCMC 链对应的模型分布更为

扩散，产生的样本差异性较大，更有利于状态空间的搜索。

 

参考文献

[1]论文： RBM学习方法对比 陆萍，陈志峰，施连敏

[2]博客：Gibbs抽样学习方法笔记  http://www.cnblogs.com/joeman/archive/2013/04/08/3008423.html

[3]博客： 对比散度：http://blog.csdn.net/itplus/article/details/19408143

[4]百度百科：模拟退火算法