基于图卷积网络(GCN)的表面缺陷识别方法(上)
Posted 徐泽玮
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于图卷积网络(GCN)的表面缺陷识别方法(上)相关的知识,希望对你有一定的参考价值。
全文综述:
首先本篇文章的目的也就是为了记录本次毕设的内容,因为发现之前的项目长时间搁置导致部分细节内容都已经忘记了,所以特此记录。如果有错误请大家批评指正。也希望可以给刚接触这方面的小白一点启发,毕竟在我刚开始的时候也是没有找到许多有用的文章。
对于本次的题目其实老师给到的参考文献很多,但是真正可以利用的资源较少,因为对于缺陷识别领域,利用图卷积神经网络的内容我没有找到特别多的信息,反而找到了我导师的文章(这就很搞),所以如果有在缺陷识别领域利用图卷积神经网络进行实验的文章或者博客也希望大家可以添加到评论区。我也会将所有的参考文献添加到最后方便大家可以去学习。
针对于缺陷识别的意义我在这里就不做过多赘述,因为这类的文章网上很多,但是其中突出的两个问题在于,1.数据集难以获取。2.运行速度较慢。因为对于实际应用而言,大量带有标签的数据是需要耗费大量的人力物力的,所以获取成本较高。其次对于实际的缺陷检测场景下,检测是需要正确且快速的,所以对于检测速度也是有要求的。所以这两点是较为棘手的两个问题。
实验部分:
我的工作主要集中在利用小数据集完成缺陷识别任务,没有着重研究改善运行速度的问题。而是将重点放到了解决数据集难以获取的问题。下面是我实验的思维导图,首先通过利用few-shot learning的思想分割数据集,然后对于图像数据进行节点嵌入(其中利用CNN网络),然后利用曼哈顿距离计算节点间的距离,利用CNN网络进行降维处理,完成图数据的建立之后,再进入
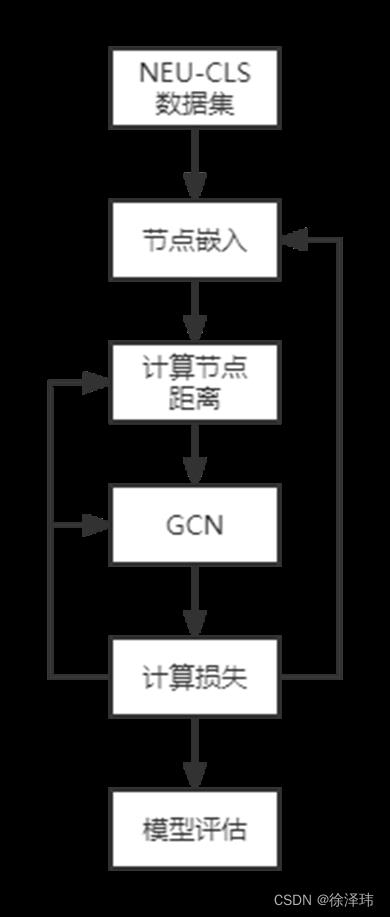
所以对于本文主要运用得就是利用小样本学习(Few-shot learning)和图卷积神经网络(GCN)解决缺陷识别问题。我的整体的实验框架的是基于我老师的一篇文章,我对于文章中的模型进行了简化。详情可以查看原论文https://www.sciencedirect.com/science/article/pii/S0736584520302933
首先对于小样本学习,大多数对于其描述都是站在只进行小样本学习的角度,而我可能会站在对于构建图数据的角度介绍小样本学习。
小样本学习(Few-shot learning):
对于小样本学习的目的是想要让模型学习到图像与图像之间的区别,而不是像监督学习,让模型认识这个图片,因为监督学习的学习思路需要大量的数据集让模型认识这个类别的特点,然而小样本学习则是在每个类别中挑选固定数量的有标签的样本,作为support set(支持集,也是传统意义上的训练集),再在整个大数据集中随机挑选一张没有标签的图像作为为query set(查询集,训练的目标)。所以一共会被挑出qK+1张图片(q代表一个类别中被挑出的图片数量,K代表类别数)。对于这qK+1张图就可以建立一个图(graph)数据。
对于我上述的关于few-shot learning的理解主要是对于Few-Shot Learning with Graph Neural Networks中对于few-shot learning介绍中所得知。下图为其中的截图。本篇文章也是图卷积神经网络用于机器视觉的一篇经典之作。

数据集介绍:
接下来简单介绍本次实验利用的数据集,其中利用的是东北大学的热轧钢表面缺陷数据集(NEU-CLS数据集),其中有6类缺陷,其中每种缺陷都有300张灰度图,每张图片的像素大小为200×200
 图数据的构建:
图数据的构建:
图数据的构建主要分为两个部分,分别为节点嵌入和节点距离计算。
节点嵌入:
在节点嵌入之前需要将图像数据进行简单的预处理,首先需要对于图像进行规范化处理,目的是为了减少对比度和光照对于图像数据的影响。
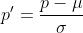
其次需要将图像数据的大小进行调整,对于之前200×200的图像,需要缩小为48×48的图像,缩小后的图像,可以加快训练的速度。
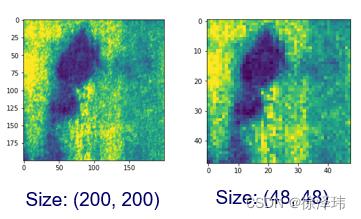
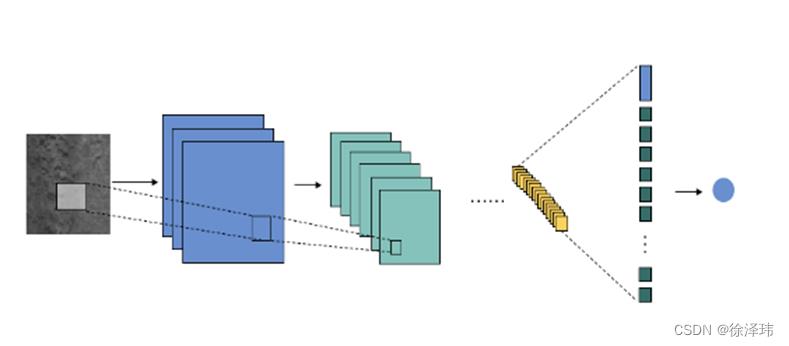
完成对于图像的预处理之后,接下来就需要将图像输入CNN网络中进行节点嵌入,下面是整个网络的具体参数,(其中网络是借鉴Few-Shot Learning with Graph Neural Networks中的节点嵌入网络)。
class Embedding(nn.Module):
def __init__(self, args):
super(Embedding, self).__init__()
self.emb_size = args.embedding_size
self.ndf = args.nf_cnn
self.args = args
# Input (48x48x1)
self.conv1 = nn.Conv2d(1, self.ndf, kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(self.ndf)
# Input (48x48x64)
self.conv2 = nn.Conv2d(self.ndf, int(self.ndf * 1.5), kernel_size=3, bias=False)
self.bn2 = nn.BatchNorm2d(int(self.ndf * 1.5))
# Input (10x10x96)
self.conv3 = nn.Conv2d(int(self.ndf * 1.5), self.ndf * 2, kernel_size=3, padding=1, bias=False)
self.bn3 = nn.BatchNorm2d(self.ndf * 2)
self.drop_3 = nn.Dropout2d(0.4)
# Input (4x4x128)
self.conv4 = nn.Conv2d(self.ndf * 2, self.ndf * 4, kernel_size=3, padding=1, bias=False)
self.bn4 = nn.BatchNorm2d(self.ndf * 4)
self.drop_4 = nn.Dropout2d(0.5)
# Input (2x2x256)
# self.fc1 = nn.Linear(self.ndf * 4 * 5 * 5, self.emb_size, bias=True)
self.fc1 = nn.Linear(self.ndf * 4 * 2 * 2, self.emb_size, bias=True) # 全连接层
# self.fc1 = nn.Linear(self.ndf * 4, self.emb_size, bias=True)
self.bn_fc = nn.BatchNorm1d(self.emb_size) # batch_normalization
def forward(self, input):
e1 = F.max_pool2d(self.bn1(self.conv1(input)), 2) # input:(48x48x1) output:(24x24x64)
x = F.leaky_relu(e1, 0.2, inplace=True)
e2 = F.max_pool2d(self.bn2(self.conv2(x)), 2) # input:(24x24x64) output:(11x11x96)
x = F.leaky_relu(e2, 0.2, inplace=True)
e3 = F.max_pool2d(self.bn3(self.conv3(x)), 2) # input:(11x11x96) output:(5x5x128)
x = F.leaky_relu(e3, 0.2, inplace=True)
x = self.drop_3(x)
e4 = F.max_pool2d(self.bn4(self.conv4(x)), 2) # input:(5x5x128) output:(2x2x256)
x = F.leaky_relu(e4, 0.2, inplace=True)
x = self.drop_4(x)
x_size = x.size()
x = x.contiguous()
x = x.view(x_size[0], -1)
output = self.bn_fc(self.fc1(x)) # output:(1 x embed_size)
return output对于节点嵌入完成的向量,需要将其one-hot编码的标签和节点的特征向量进行合并,对于未知标签的图像,利用0进行填充。
计算节点距离:
对于节点距离的计算,首先需要明确,在构建图(graph)数据的时候,没有先验知识来指导哪些节点要和特定的另外的节点相连接或者不相连,所以最简单粗暴的方法就是将所有节点都一一相连,即构建一个全连接图,每一个节点需要和其余所有节点进行连接,所以利用曼哈顿距离,将节点的特征向量进行计算所以构建出来的距离矩阵应该是一个(节点个数,节点个数,embedding_size)大小的矩阵。
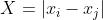
所以计算完节点的距离之后,整体的图数据就构建完成了,图数据所需要的节点特征,以及邻接矩阵都已经计算完成,所以之后就要对于图卷积实现了。下面将会详细介绍如何完成对于图卷积网络的实现以及之后需要对于网络框架进行的改善。
 开发者涨薪指南
开发者涨薪指南
 48位大咖的思考法则、工作方式、逻辑体系
48位大咖的思考法则、工作方式、逻辑体系
以上是关于基于图卷积网络(GCN)的表面缺陷识别方法(上)的主要内容,如果未能解决你的问题,请参考以下文章
论文解读丨基于局部特征保留的图卷积神经网络架构(LPD-GCN)