栈练习之Example002-求后缀式的数值
Posted 二木成林
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了栈练习之Example002-求后缀式的数值相关的知识,希望对你有一定的参考价值。
Example002
题目
编写一个函数,求后缀式的数值,其中后缀式存于一个字符数组 exp 中,exp 中最后一个字符为 "\\0",作为结束符,并且假设后缀式中的数字都只有一位。本题中所出现的除法运算,皆为整除运算,如 2/3 结果为 0,3/2 结果为 1。
分析
前缀、中缀和后缀表达式是对表达式的不同记法,其区别在于运算符相对于操作数的位置不同,其中前缀表达式的运算符位于操作数的前面,后缀表达式的运算符位于操作数的后面。例如:
- 中缀表达式:
1+(2+3)*4-5。 - 前缀表达式:
-+1*+2345。 - 后缀表达式:
123+4*+5-。
后缀表达式的计算机求值的算法思想:与前缀表达式的计算类似,只是顺序是从左向右扫描表达式。如果遇到数字,则将数字压入栈中;如果遇到运算符,则弹出栈顶的两个数字,用运算符对它们做相应的计算,并且将计算结果压入栈中。重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果。
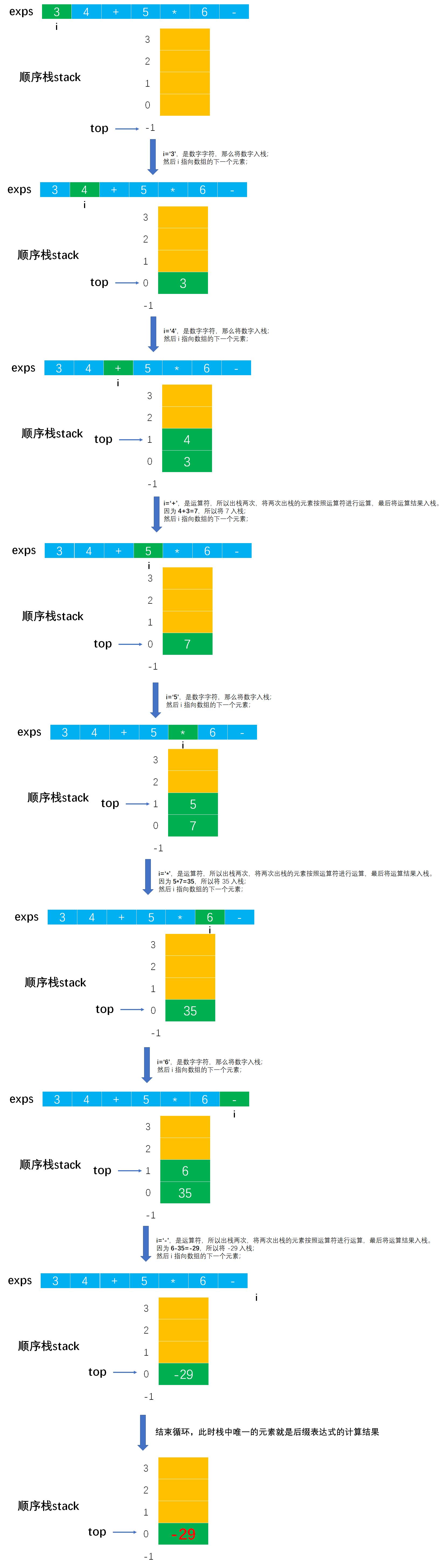
例如,有后缀表达式:34+5*6-。求值步骤如下:
- (1)从左往右扫描,将 3 和 4 压入栈中。
- (2)遇到
+运算符,因此弹出栈顶的两个元素,分别是 3 和 4(其中 4 是栈顶元素、3 是次栈顶元素),计算3+4的值,得到结果 7,再将 7 入栈。 - (3)遇到数字 5,然后将 5 入栈。
- (4)接下来是
*字符,因此弹出栈顶的两个元素,分别是 5 和 7,计算5*7的值,得到结果 35,将 35 入栈。 - (5)遇到数字 6,然后将 6 入栈。
- (6)最后是
-运算符,计算出6-35的值,即 -29,由此得出最终结果。
更多关于后缀表达式请参考:Note001-前缀和中缀及后缀表达式
图解
以 34+5*6- 为例如图所示:
C实现
核心代码:
/**
* 根据运算符计算两数的结果
* @param sign 运算符
* @param a 第一个数
* @param b 第二个数
* @return 两数计算的结果
*/
int evaluate(char sign, int a, int b)
int result = 0;
switch (sign)
case '+':
result = a + b;
break;
case '-':
result = a - b;
break;
case '*':
result = a * b;
break;
case '/':
result = a / b;
break;
case '%':
result = a % b;
break;
default:
printf("非可计算的运算符:%c", sign);
break;
return result;
/**
* 计算前缀表达式
* @param exps 前缀表达式,以 '\\0' 字符结束
* @param n 字符数组的实际字符个数
* @return 表达式的计算结果
*/
int evaluateSuffixExpression(char exps[], int n)
// 0.解题需要用到栈,所以创建顺序栈并初始化栈
SeqStack stack;
init(&stack);
// 1.从左往右扫描后缀表达式,所以要正序遍历字符数组
for (int i = 0; i < n; i++)
// 1.1 如果当前字符是数字字符
if (exps[i] >= '0' && exps[i] <= '9')
// 1.1.1 则将该数字压入栈中,注意数字字符要转换成数字才能存入栈中,而数字字符要转换成数字可以用数字字符减去'0'字符即可得到所对应的数字
push(&stack, exps[i] - '0');
// 1.2 如果当字符不是数字字符,而是运算符
else
// 1.2.1 那么弹出栈顶两个数字,用 a 和 b 来保存
int a, b;
pop(&stack, &a);
pop(&stack, &b);
// 1.2.2 根据运算符调用函数计算 a 和 b 的结果
int result = evaluate(exps[i], a, b);
// 1.2.3 将计算结果压入栈中
push(&stack, result);
// 2.最终结果也是存在栈中的,就算栈顶元素,所以获得栈顶元素返回即可
int top;
getTop(stack, &top);
return top;
完整代码:
#include <stdio.h>
/**
* 顺序栈最大存储的元素个数
*/
#define MAXSIZE 100
/**
* 顺序栈结构体定义
*/
typedef struct
/**
* 数据域,数组,用来存储栈中元素
*/
int data[MAXSIZE];
/**
* 指针域,表示栈顶指针,实际上就是数组下标
*/
int top;
SeqStack;
/**
* 初始化顺序栈,即将栈顶指针指向 -1 表示空栈
* @param stack 顺序栈
*/
void init(SeqStack *stack)
// 设定让栈顶指针指向 -1 表示为栈空
stack->top = -1;
/**
* 将元素入栈
* @param stack 顺序栈
* @param ele 元素值
* @return 如果栈满则返回 0 表示入栈失败;如果插入成功则返回 1
*/
int push(SeqStack *stack, int ele)
// 1.参数校验,如果栈满则不能入栈元素
if (stack->top == MAXSIZE - 1)
// 如果栈满,则返回 0,表示不能入栈
return 0;
// 2.先将栈顶指针加一,指向新空数组位置
stack->top++;
// 3.将新元素值填充到新位置中
stack->data[stack->top] = ele;
return 1;
/**
* 将元素出栈
* @param stack 顺序栈
* @param ele 用来保存出栈的元素
* @return 如果栈空则返回 0 表示出栈失败;否则返回 1 表示出栈成功
*/
int pop(SeqStack *stack, int *ele)
// 1.参数校验,栈空不能出栈
if (stack->top == -1)
// 栈空,没有元素可出栈
return 0;
// 2.用 ele 来保存顺序栈栈顶元素
*ele = stack->data[stack->top];
// 3.然后栈顶指针减一,表示出栈一个元素
stack->top--;
return 1;
/**
* 获取栈顶元素,但不出栈
* @param stack 顺序栈
* @param ele 用来保存出栈元素
* @return 如果栈空则返回 0 表示出栈失败;否则返回 1 表示出栈成功
*/
int getTop(SeqStack stack, int *ele)
// 1.参数校验,如果栈空则不能出栈
if (stack.top == -1)
// 栈空,没有元素可出栈
return 0;
// 2.保存栈顶元素返回
*ele = stack.data[stack.top];
return 1;
/**
* 根据运算符计算两数的结果
* @param sign 运算符
* @param a 第一个数
* @param b 第二个数
* @return 两数计算的结果
*/
int evaluate(char sign, int a, int b)
int result = 0;
switch (sign)
case '+':
result = a + b;
break;
case '-':
result = a - b;
break;
case '*':
result = a * b;
break;
case '/':
result = a / b;
break;
case '%':
result = a % b;
break;
default:
printf("非可计算的运算符:%c", sign);
break;
return result;
/**
* 计算前缀表达式
* @param exps 前缀表达式,以 '\\0' 字符结束
* @param n 字符数组的实际字符个数
* @return 表达式的计算结果
*/
int evaluateSuffixExpression(char exps[], int n)
// 0.解题需要用到栈,所以创建顺序栈并初始化栈
SeqStack stack;
init(&stack);
// 1.从左往右扫描后缀表达式,所以要正序遍历字符数组
for (int i = 0; i < n; i++)
// 1.1 如果当前字符是数字字符
if (exps[i] >= '0' && exps[i] <= '9')
// 1.1.1 则将该数字压入栈中,注意数字字符要转换成数字才能存入栈中,而数字字符要转换成数字可以用数字字符减去'0'字符即可得到所对应的数字
push(&stack, exps[i] - '0');
// 1.2 如果当字符不是数字字符,而是运算符
else
// 1.2.1 那么弹出栈顶两个数字,用 a 和 b 来保存
int a, b;
pop(&stack, &a);
pop(&stack, &b);
// 1.2.2 根据运算符调用函数计算 a 和 b 的结果
int result = evaluate(exps[i], a, b);
// 1.2.3 将计算结果压入栈中
push(&stack, result);
// 2.最终结果也是存在栈中的,就算栈顶元素,所以获得栈顶元素返回即可
int top;
getTop(stack, &top);
return top;
int main()
char prefixExp[] = "34+5*6-";
int n = 7;
int result;
result = evaluateSuffixExpression(prefixExp, n);
printf("后缀表达式计算结果:%d", result);
执行结果:
后缀表达式计算结果:-29
Java实现
核心代码:
/**
* 求后缀表达式的值
*
* @param exps 后缀表达式字符序列
* @return 表达式的计算结果
* @throws Exception 如果栈满再入栈则会抛出此异常
*/
public static int evaluateSuffixExpression(char exps[]) throws Exception
// 0.解题需要用到栈,所以创建顺序栈并初始化栈
SeqStack stack = new SeqStack();
stack.init();
// 变量,记录字符序列的长度
int n = exps.length;
// 1.从左往右扫描后缀表达式,所以要正序遍历字符数组
for (int i = 0; i < n; i++)
// 1.1 如果当前字符是数字字符
if (exps[i] >= '0' && exps[i] <= '9')
// 1.1.1 则将该数字压入栈中,注意数字字符要转换成数字才能存入栈中,而数字字符要转换成数字可以用数字字符减去'0'字符即可得到所对应的数字
stack.push(exps[i] - '0');
// 1.2 如果当字符不是数字字符,而是运算符
else
// 1.2.1 那么弹出栈顶两个数字,用 a 和 b 来保存
int a = stack.pop();
int b = stack.pop();
// 1.2.2 根据运算符调用函数计算 a 和 b 的结果
int result = evaluate(exps[i], a, b);
// 1.2.3 将计算结果压入栈中
stack.push(result);
// 2.最终结果也是存在栈中的,就算栈顶元素,所以获得栈顶元素返回即可
return stack.getTop();
/**
* 根据运算符计算两数的结果
*
* @param sign 运算符
* @param a 第一个数
* @param b 第二个数
* @return 两数计算的结果
*/
private static int evaluate(char sign, int a, int b) throws Exception
int result = 0;
switch (sign)
case '+':
result = a + b;
break;
case '-':
result = a - b;
break;
case '*':
result = a * b;
break;
case '/':
result = a / b;
break;
case '%':
result = a % b;
break;
default:
throw new Exception("非可计算的运算符:" + sign);
return result;
完整代码:
public class Test
public static void main(String[] args) throws Exception
String prefixExp = "34+5*6-";
// 调用函数计算后缀表达式
int result;
result = evaluateSuffixExpression(prefixExp.toCharArray());
System.out.println("后缀表达式计算结果:" + result);
/**
* 求后缀表达式的值
*
* @param exps 后缀表达式字符序列
* @return 表达式的计算结果
* @throws Exception 如果栈满再入栈则会抛出此异常
*/
public static int evaluateSuffixExpression(char exps[]) throws Exception
// 0.解题需要用到栈,所以创建顺序栈并初始化栈
SeqStack stack = new SeqStack();
stack.init();
// 变量,记录字符序列的长度
int n = exps.length;
// 1.从左往右扫描后缀表达式,所以要正序遍历字符数组
for (int i = 0; i < n; i++)
// 1.1 如果当前字符是数字字符
if (exps[i] >= '0' && exps[i] <= '9')
// 1.1.1 则将该数字压入栈中,注意数字字符要转换成数字才能存入栈中,而数字字符要转换成数字可以用数字字符减去'0'字符即可得到所对应的数字
stack.push(exps[i] - '0');
// 1.2 如果当字符不是数字字符,而是运算符
else
// 1.2.1 那么弹出栈顶两个数字,用 a 和 b 来保存
int a = stack.pop();
int b = stack.pop();
// 1.2.2 根据运算符调用函数计算 a 和 b 的结果
int result = evaluate(exps[i], a, b);
// 1.2.3 将计算结果压入栈中
stack.push(result);
// 2.最终结果也是存在栈中的,就算栈顶元素,所以获得栈顶元素返回即可
return stack.getTop();
/**
* 根据运算符计算两数的结果
*
* @param sign 运算符
* @param a 第一个数
* @param b 第二个数
* @return 两数计算的结果
*/
private static int evaluate(char sign, int a, int b) throws Exception
int result = 0;
switch (sign)
case '+':
result = a + b;
break;
case '-':
result = a - b;
break;
case '*':
result = a * b;
break;
case '/':
result = a / b;
break;
case '%':
result = a % b;
break;
default:
throw new Exception("非可计算的运算符:" + sign);
return result;
SeqStack:
public class SeqStack
/**
* 常量,顺序栈所能容纳的最大元素个数
*/
private final int MAXSIZE = 100;
/**
* 声明一个顺序栈
*/
private Stack stack;
/**
* 初始化顺序栈
*/
public void init()
// 实例化栈对象
stack = new Stack();
// 为数据域分配空间
stack.data = new int[MAXSIZE];
// 将顺序栈的栈顶指针指向 -1 表示空栈
stack.top = -1;
/**
* 判断顺序栈是否为空
*
* @return 如果顺序栈为空则返回 true,否则返回 false
*/
public boolean isEmpty()
// 规定了 -1 表示空栈,所以只需要判断栈顶指针是否等于 -1 即可
return stack.top == -1;
/**
* 将指定元素入栈
*
* @param ele 指定元素
* @throws Exception 如果栈满则不能入栈,抛出此异常
*/
public void push(int ele) throws Exception
// 1.参数校验,如果栈满则不能入栈,抛出异常
if (stack.top == MAXSIZE - 1) // 因为栈顶指针 top 存储的是数组下标,所以判断是否等于 MAXSIZE-1
throw new Exception("栈已满,不能再插入!");
// 2.先栈顶指针加 1,因为原栈顶指针处已经存储了元素,所以加一指向新的空位置
stack.top++;
// 3.在新的空位置处插入新元素,即为指定下标的数组元素赋值
stack.data[stack.top] = ele;
/**
* 将栈顶元素出栈
*
* @return 栈顶元素
* @throws Exception 如果栈空则不能出栈,抛出此异常
*/
public int pop() throws Exception
// 1.参数校验,如果栈空则不能出栈,抛出异常
if (stack.top == -1) // 因为栈空的定义是栈顶指针为 -1,所以如果栈顶指针为 -1 那么就是空栈,就不能出栈元素
throw new Exception("栈为空,不能出栈元素!");
// 2.记录栈顶元素,因为要将该元素返回,即要出栈的元素
int result = stack.data[stack.top];
// 3.栈顶指针减一,因为原栈顶元素已经出栈了,栈中元素个数减一
stack.top--;
return result;
/**
* 获取栈顶元素,但不出栈
*
* @return 栈顶元素
* @throws Exception 如果栈空则不能出栈,抛出此异常
*/
public int getTop() throws Exception
// 1.参数校验,如果栈空则不能出栈,抛出异常
if (stack.top == -1)
throw new Exception("栈为空,不能获取栈顶元素!");
// 2.直接返回栈顶元素,但不出栈
return stack.data[stack.top];
/**
* 顺序栈中元素个数
*
* @return 栈中元素个数
*/
public int size()
// top 表示栈顶指针,实际上就是数组 data 的下标,所以实际元素个数就是下标加一
// 即使是空栈 top=-1,那么最后也会返回 0 表示元素个数为零个
return stack.top + 1;
/**
* 打印顺序栈中所有元素,从栈顶到栈底
*/
public void print()
System.out.print("[");
for (int i = stack.top; i >= 0; i--)
if (i != stack.top)
System.out.print(", ");
System.以上是关于栈练习之Example002-求后缀式的数值的主要内容,如果未能解决你的问题,请参考以下文章
栈练习之Example003-用不带头结点的单链表存储链栈并实现栈相关算法
栈练习之Example005-检查一个程序中的花括号方括号和圆括号是否配对