Python数据结构与算法（4.2）——递归的可视化

Posted 2022-04-18 盼小辉丶

Python数据结构与算法（4.2）——递归的可视化

• • 0. 学习目标
  • 1 递归的调用
  • 2 递归可视化
  • • 2.1 turtle 库简介
    • 2.1 递归绘图
  • 相关链接

0. 学习目标

递归函数是直接调用自己或通过一系列语句间接调用自己的函数。递归在程序设计有着举足轻重的作用，在很多情况下，借助递归可以优雅的解决问题。虽然使用递归可以快速的解决一些难题，但由于递归的抽象性，使递归难以掌握。为了更好的理解递归函数背后的思想，本节主要通过可视化方式来了解递归函数的执行步骤。
通过本节学习，应掌握以下内容：

• 提高对递归的理解
• 利用可视化理解递归函数背后的思想

1 递归的调用

虽然使用递归可以快速的解决一些难题，但由于递归的抽象性，使得递归难以掌握。虽然已经在《递归基础》中讲解了递归的示例，并且简单的了解了递归的调用过程，但缺乏具体的认知。本节将对递归的调用进行更加深入的讲解。
递归函数执行时，每次递归调用都会在内存中创建新的函数副本，一旦函数调用结束，则返回一些数据，并将此副本就会从内存中删除。通常，递归方法得到的解决方案看起来十分简洁简单，但理解并跟踪函数的执行却较为复杂。为了更好地理解，考虑以下求取斐波那契数列的简单示例：

def fibo(n):
    if n == 0:
        return 1
    else:
        return n * fibo(n - 1)
def main():
    number = 4
    result = fibo(number)
    print(result)
if __name__ == "__main__":
    main()

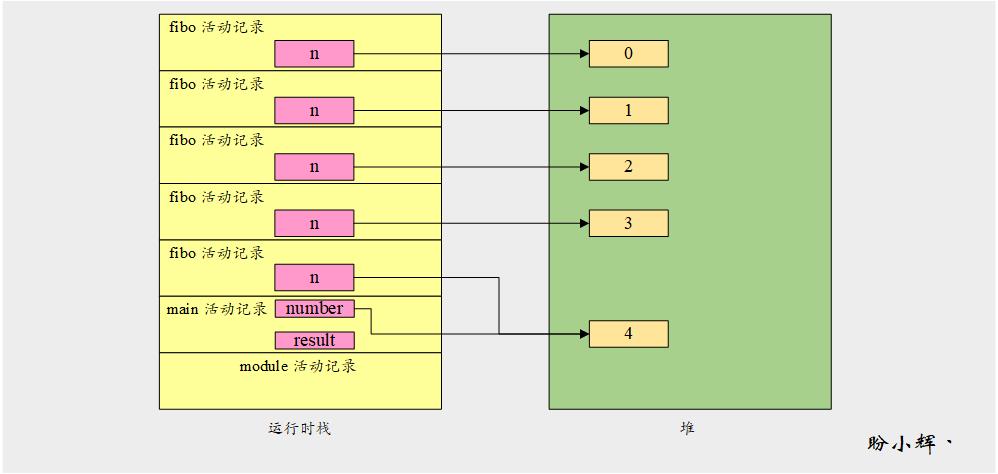
当程序运行到第 10 行时。第一次调用 fibo() 函数，会为 fibo() 函数调用创建一条新的活动记录，此时在运行时栈上具有 3 条活动记录。然后 Python 解释器跳转到第 2 行，其中 n 指向数字 4，如下图所示。n 不等于 0，因此跳转到第 5 行，其中包含一个对 fibo() 的函数调用，这将在运行时堆栈上创建另一个活动记录。重复上述过程，直到 n=0。
需要注意的是，每个递归函数调用都有一个变量 n 的副本。活动记录保存函数范围内的所有局部变量和参数。每次调用函数时，都会创建一个新的活动记录，并将局部变量的新副本存储在活动记录中，程序运行过程的调用顺序如下图所示：

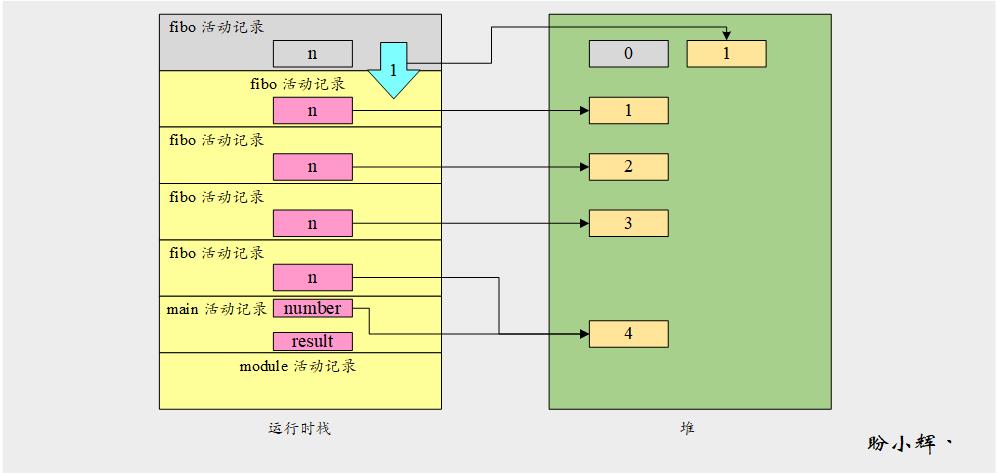
当函数执行到 n=0 时，fibo() 函数返回了它的第一个值，它将 1 返回到上一个函数调用。如下图所示，从运行时堆栈中弹出 n=0 时函数调用的活动记录(通过将图中活动记录的变为灰色来表示)。当函数返回时，活动记录的空间被回收以供以后使用。堆上的阴影对象 0 也被垃圾收集器回收，因为不再有指向它的引用。

在第一次 fibo() 函数返回之后，Python 解释器返回到前一个函数调用中的第 5 行，这个语句也包含一个 return 语句，所以函数再次返回到第 5 行，返回值为 1。同样，函数再次返回，但这次的值为 2。按照上述过程，直到 fibo() 函数返回到 main() 函数的第 8 行，整个过程如下图所示：

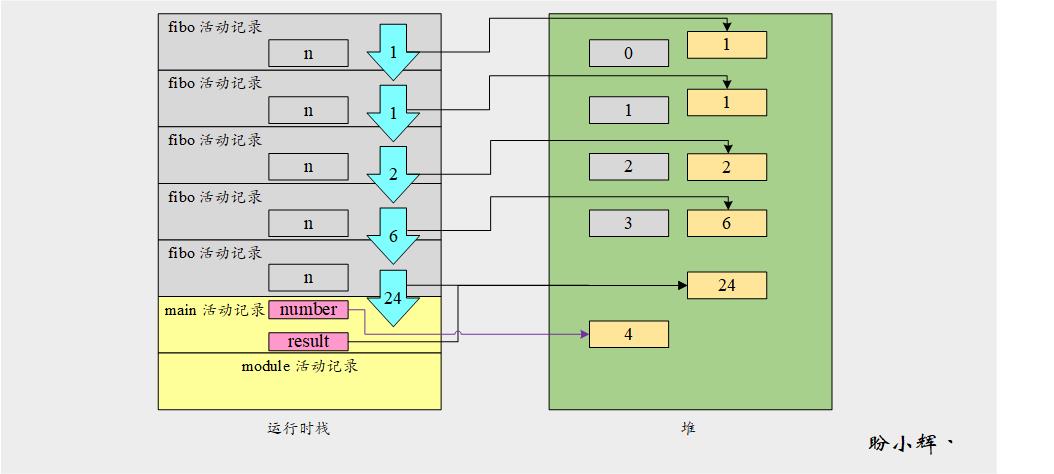
最后，程序打印执行结果，在第 9 行之后从 main() 函数返回，在第 11 行后从 module 返回并终止。从以上示例可以看出，对 fibo() 函数的每次递归调用都会创建自己的变量副本。每次调用该函数时，都会将局部变量和参数复制到相应的活动记录中。当函数调用返回时，相应的活动记录会从运行时堆栈中弹出。这就是递归函数的执行方式。

2 递归可视化

本节将利用 turtle 库递归的绘制图案，提高对递归过程的认识。

2.1 turtle 库简介

turtle 库属于是python的标准库，通常用于绘制图案，可以使用该库创建一只小乌龟 (turtle) 在画布上移动，当小乌龟爬行时会在画布上绘制线条，而当前尾巴抬起时，并不会进行绘制。

接下来，我们将介绍一些基本的 turtle 绘图函数：

• turtle.penup(): turtle 抬起尾巴，之后的移动并不在图上进行绘制
• turtle.pendown()：turtle 放下尾巴，开始爬行，之后会在图上绘制其行动轨迹
• turtle.pensize(width)：用于改变画笔的宽度
• turtle.pencolor(color)：用于改变画笔颜色
• turtle.forward(distance)：向前移动 distance
• turtle.back(distance)：向后移动 distance

2.1 递归绘图

首先通过创建一个简单的递归函数 draw() 来了解 turtle 库，这个递归函数的基本情况为——要画的线长 distance 降为 0；若线长大于 0，就让小乌龟小乌龟向前绘制 distance 个单位距离，然后左转 30 度；递归情况为——缩短后的距离再次调用 draw() 函数。

# 导入 turtle 库
import turtle
# 创建小乌龟对象
my_turtle = turtle.Turtle()
# 创建用户绘制图案的窗口
window = my_turtle.getscreen()

def draw(turtle, distance):
    if distance > 0:
        # 小乌龟向前绘制 distance 个单位距离
        turtle.forward(distance)
        # 然后左转 30 度
        turtle.left(30)
        draw(turtle, distance-6)
draw(my_turtle, 200)
window.exitonclick()

接下来，我们使用 turtle 模块绘制分形树。分形树和递归有许多的共同点，是数学中的一个概念，无论放大多少倍观察分形图，总能看到相同的基本形状。
如果我们定义树为包含向左生长的子树和向右生长的子树的话，就可以根据递归的思想得到分形树：

import turtle
def tree(branch, turtle):
    if branch > 5:
        turtle.forward(branch)
        turtle.right(20)
        tree(branch-15, turtle)
        turtle.left(40)
        tree(branch-10, turtle)
        turtle.right(20)
        turtle.backward(branch)
my_turtle = turtle.Turtle()
window = my_turtle.getscreen()
my_turtle.left(90)
my_turtle.up()
my_turtle.backward(300)
my_turtle.down()
tree(110, my_turtle)
window.exitonclick()

相关链接

递归基础概念