树的存储结构的设计及递归遍历(前序,后序,层序)算法实现——Java数据结构与算法笔记
Posted stormzhuo
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了树的存储结构的设计及递归遍历(前序,后序,层序)算法实现——Java数据结构与算法笔记相关的知识，希望对你有一定的参考价值。
文章目录
一、树
再对树的存储结构设计以及相关操作(遍历)算法实现之前，需要对树的定义和相关术语要有所了解，下面分别对这些进行简单的介绍
1. 树的定义
树：n (n ≥ 0 )个结点的有限集合，当n = 0时，称为空树;任意一棵非空树T满足以下条件︰
- 有且仅有一个特定的称为根的结点;
- 当
n > 1时，除根结点之外的其余结点被分成m ( m > 0）个互不相交的有限集合T1,T2… ,Tm，其中每个集合又是一棵树，并称为这个根结点的子树。
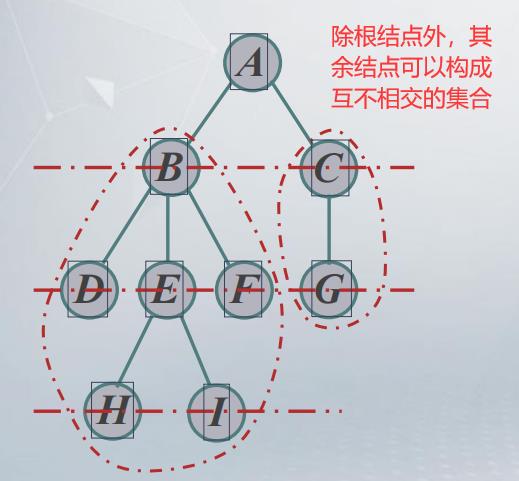
互不相交的具体含义是什么?
结点： 结点不能属于多个子树
边： 子树之间不能有关系
如下所示的都是相交的，故不是树
2. 树的基本术语
结点的度： 结点所拥有的子树的个数
树的度： 树中各结点度的最大值
叶子结点： 度为 0 的结点，也称为终端结点
分支结点： 度不为 0 的结点，也称为非终端结点
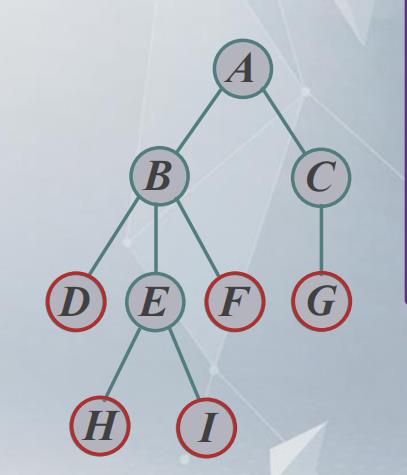
如下所示的树，
- 结点A有两个子树B,C,故结点A的度为2。
- 树中最大的度为B，即有三个子树，故树的度为3。
- 红色结点的度为0，故红色结点是叶子节点，也叫终端结点
- 非红色结点的度不为0，故非红色结点的为非终端结点
孩子： 树中某结点的子树的根结点称为这个结点的孩子结点
双亲： 这个结点称为它孩子结点的双亲结点
兄弟： 具有同一个双亲的孩子结点互称为兄弟
如下所示的图，结点B是结点A的孩子结点，反之，结点A是结点B双亲结点，结点C和结点B互为兄弟
类比法：
- 在线性结构中，逻辑关系表现为前驱——后继
- 在树结构中，逻辑关系表现为双亲——孩子
路径： 结点序列 n1, n2, …, nk 称为一条由 n1 至 nk 的路径，当且仅当满足如下关系：结点 ni是 ni+1 的双亲（1<=i<k）
路径长度： 路径上经过的边的个数
祖先、子孙： 如果有一条路径从结点 x 到结点 y， 则 x 称为 y 的祖先，而 y 称为 x 的子孙
如下所示的图中
- 结点序列A,B,E,H称为一条由A到H的一条路径
- 路径上经过的边为3，故路径长度为3
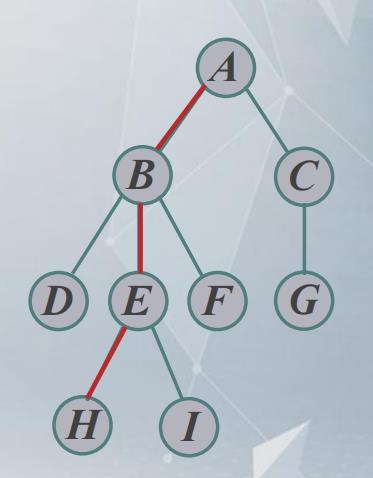
在树结构中，路径是唯一的
结点所在层数： 根结点的层数为 1；对其余结点，若某结点在第 k 层，则其孩子结点在第 k+1 层
树的深度（高度）： 树中所有结点的最大层数
树的宽度： 树中每一层结点个数的最大值
如下图所示
3. 树的遍历
什么是遍历？线性结构如何遍历？
简言之，遍历是对数据集合进行没有遗漏、没有重复的访问
树的遍历： 从根结点出发，按照某种次序访问树中所有结点，并且每个结点仅被访问一次
3.1 先序遍历
若树为空，则空操作返回；否则
- 访问根结点
- 从左到右前序遍历根结点的每一棵子树
例如如下图的前序遍历序列为：A，B，D，H，I，E，J，C，F，K，G
3.2 后序遍历
若树为空，则空操作返回；否则
- 从左到右后序遍历根结点的每一棵子树
- 访问根结点
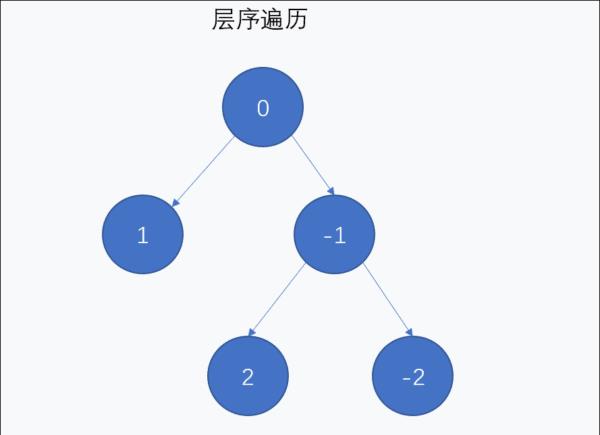
3.3 层序遍历
从树的根结点开始，自上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问
4. 树的存储结构
实现树的存储结构，关键是什么?
如何表示树中结点之间的逻辑关系
什么是存储结构?
数据元素及其逻辑关系在存储器中的表示
树中结点之间的逻辑关系是什么?
思考问题的出发点：如何表示结点的双亲和孩子
4.1 双亲表示法
用一维数组存储树中各个结点（一般按层序存储）的数据信息以及该结点的双亲在数组中的下标
4.1.1 代码实现
4.1.1.1 树的存储结构设计
结点数据结构
// 树的结点的数据结构
public class ParentNode<T>
// 存储结点的数据
private T data;
// 存储结点的双亲结点的下标
private int parent;
public ParentNode()
public ParentNode(T data, int parent)
this.data = data;
this.parent = parent;
public void setData(T data)
this.data = data;
public T getData()
return data;
public void setParent(int parent)
this.parent = parent;
public int getParent()
return parent;
树的数据结构及初始化
public class Tree<T>
// 存储树所有结点的数组
private ParentNode[] parentNodes;
// 结点个数
private int nodeNum;
// 构造空的树
public Tree(int size)
// 创建指定容量的树
parentNodes = new ParentNode[size];
// 所有结点的数据和结点的双亲下标分别初始化为“#”，-1，代表结点为空。
for (int i = 0; i < size; i++)
parentNodes[i] = new ParentNode("#", -1);
// 结点个数初始化为0
nodeNum = 0;
以下给出的代码都是Tree类的成员方法
4.1.1.2 树的建立
树的建立
需要提供一个方法在数组中添加树的结点，由于此时树为空，因此还没有树的结点的双亲，故此方法是只需要添加树的结点的数据域，而不需要添加结点的双亲域，代码如下
// 插入树的结点，不包含结点双亲的下标
public boolean insertNode(T data)
if (data != "#")
parentNodes[nodeNum++].setData(data);
return true;
return false;
当添加完树的结点的数据后，数组就有了树的结点的双亲，因此需要一个函数来添加树的结点的双亲域来找到双亲的位置，代码如下
// 给树的结点插入它的双亲的下标，第1个参数为双亲结点数据，第2个参数为孩子结点数据
public boolean insertParent(T parentData, T childData)
int parentPlace = -1;
int childPlace = -1;
// 遍历数组，找到双亲，孩子在数组中的下标
for (int i = 0; i < nodeNum; i++)
if (parentNodes[i].getData().equals(parentData))
parentPlace = i;
if (parentNodes[i].getData().equals(childData))
childPlace = i;
// 把孩子结点的双亲下标数据指向双亲的在数组的位置
if (parentPlace != -1 && childPlace != -1)
parentNodes[childPlace].setParent(parentPlace);
return true;
return false;
4.1.1.3 树的递归遍历算法设计（先序，后序)
树的递归遍历
先序遍历
根据树先序遍历的操作定义，访问根结点的操作发生在该结点的子树遍历之前，所以，先序遍历的递归实现只需将输出操作System.out.print放到递归遍历子树之前即可，代码如下
// 先序遍历，参数为根结点下标
public void preOrder(int i)
if (nodeNum != 0)
// 先输出根结点数据
System.out.print(parentNodes[i].getData() + " ");
/* 遍历数组，找到根结点的子树，以此子树为根结点调用递归输出子结点数据
由于采用层序序列构建树，所以先找到的是根结点的左子树，满足先序遍历*/
for (int j = 0; j < nodeNum; j++)
if (parentNodes[j].getParent() == i)
preOrder(j);
后序遍历
根据树后序遍历的操作定义，访问根结点的操作发生在该结点的子树均遍历完毕，所以，后序遍历的递归实现只需将输出操作System.out.print放到递归遍历子树之后即可，代码如下
public void postOrder(int i)
if (nodeNum != 0)
for (int j = 0; j < nodeNum; j++)
if (parentNodes[j].getParent() == i)
postOrder(j);
System.out.print(parentNodes[i].getData() + " ");
4.1.1.4 队列实现层序遍历
层序遍历(队列实现)
在进行层序遍历时,结点访问应遵循“从上至下、从左至右”逐层访问的原则,使得先被访问结点的孩子先于后被访问结点的孩子被访问。
为保证这种“先先”的特性,可应用队列作为辅助结构。首先根结点入队,队头出队,输出出队结点,出队结点的左右孩子分别入队，以此类推，直至队列为空
例如如下图的所示的树
层序遍历的执行过程如下所示
代码如下
public void levelOrder(int i)
if (nodeNum != 0)
// 创建队列存储结点
Queue<ParentNode> queue = new LinkedList<>();
// 根结点先入队
queue.offer(parentNodes[i]);
while (!queue.isEmpty()) // 队列非空
// 出队，取出队头结点
ParentNode parentNode = queue.poll();
// 输出队头结点的数据域
System.out.print(parentNode.getData() + " ");
/* 遍历数组，找到根结点的所有孩子，并将孩子入队
* 遍历完数组后执行下一次while循环，执行同样的操作*/
for (int j = 1; j < nodeNum; j++)
if (parentNodes[parentNodes[j].getParent()] == parentNode)
queue.offer(parentNodes[j]);
4.1.1.5 测试
测试如下图树的先序遍历，后序遍历，层序遍历
测试代码
@Test
public void test()
// 创建结点容量为10的树
Tree<String> tree = new Tree<>(10);
// 以层序序列插入结点
tree.insertNode("A");
tree.insertNode("B");
tree.insertNode("C");
tree.insertNode("D");
tree.insertNode("E");
tree.insertNode("F");
tree.insertNode("G");
tree.insertNode("H");
tree.insertNode("I");
// 插入结点的双亲域，指明双亲在数组中的位置，第1参数是双亲的结点值，第2参数是双亲的孩子结点值
tree.insertParent("#", "A");
tree.insertParent("A", "B");
tree.insertParent("A", "C");
tree.insertParent("B", "D");
tree.insertParent("B", "E");
tree.insertParent("B", "F");
tree.insertParent("C", "G");
tree.insertParent("E", "H");
tree.insertParent("E", "I");
System.out.println("前序遍历");
tree.preOrder(0);
System.out.println("\\n后序遍历");
tree.postOrder(0);
System.out.println("\\n层序遍历");
tree.levelOrder(0);
测试效果
4.1.2 复杂度分析
查找结点的双亲结点的时间复杂度： 数组每一个元素不仅存储的结点的数据，还存储了此结点的双亲在数组的下标，故查找当前结点的双亲结点的时间复杂度为O(1)
查找结点的孩子结点的时间复杂度： 由于数组并没有存储结点的孩子结点信息，要想找到结点的孩子结点，只能遍历数组，最坏情况下，时间复杂度为O(n)
总结： 显然双亲表示法适合与查找双亲结点，不适合与查找孩子结点，下面介绍一种适合查找孩子结点的孩子表示法，即时间复杂度为O(1)
4.2 孩子表示法
树的孩子表示法是一种基于链表+数组的存储方法,即把每个结点的孩子排列起来,看成一个线性表,且以单链表存储,称为该结点的孩子链表,所以n个结点共有n个孩子链表(叶子结点的孩子链表为空表)。
n个孩子链表共有n个头引用(头指针）,这n个头引用又构成了一个线性表,为了便于进行查找操作,可采用顺序存储(数组实现）。
最后,将存放n个头引用的数组和存放n个结点数据信息的数组结合起来,构成孩子链表的表头数组。
在孩子表示法中存在两类结点:孩子结点和表头结点,其结点结构如下图所示(表头数组的建立是以层序序列建立的)
4.2.1 代码实现
4.2.1.1 树的存储结构设计
孩子结点的数据结构
public class ChildNode
// 存放孩子结点在数组的下标
private int child;
// 连接孩子的兄弟结点的指针，指向下一个兄弟
private ChildNode next;
public ChildNode()
public ChildNode(int child, ChildNode next)
this.child = child;
this.next = next;
public int getChild()
return child;
public void setChild(int child)
this.child = child;
public ChildNode getNext()
return next;
public void setNext(ChildNode next)
this.next = next;
结点(表头结点)的数据结构
public class TreeNode
// 存放结点的数据
private String data;
// 表头结点
private ChildNode firstNode;
public TreeNode()
public TreeNode(String data, ChildNode firstNode)
this.data = data;
this.firstNode = firstNode;
public String getData()
return data;
public void setData(String data)
this.data = data;
public ChildNode getFirstNode()
return firstNode;
public void setFirstNode(ChildNode firstNode)
this.firstNode = firstNode;
树的数据结构及初始化
// 树的数据结构
public class Tree
// 存放结点(表头)的数组
private TreeNode[] treeNodes;
// 结点个数
private int nodeNum;
Scanner scanner = new Scanner(System.in);
// 构造空的树
public Tree()
System.out.print("请输入树的结点容量:");
int size = scanner.nextInt();
// 创建指定容量的树
treeNodes = new TreeNode[size];
for (int i = 0; i < size; i++)
treeNodes[i] = new TreeNode("#", new ChildNode());
treeNodes[i].getFirstNode().setNext(null);
// 结点个数初始化为0
nodeNum = 0;
以下给出的代码都是Tree类的成员方法
4.2.1.2 树的建立
树的建立（按层序序列建立)
public void AddTreeNode()
System.out.print("请输入结点数量:");
int n = scanner.nextInt();
System.out.print("请输入结点数据:");
for (int i = 0; i < n; i++)
String c = scanner.next();
treeNodes[i].setData(c);
nodeNum++;
for (int i = 0; i < n; i++)
String data = (String)treeNodes[i].getData();
System.out.printf("%c [%d]\\n", data.charAt(0), i);
for (int i = 0; i < n; i++)
ChildNode preNode = treeNodes[i].getFirstNode(以上是关于树的存储结构的设计及递归遍历(前序,后序,层序)算法实现——Java数据结构与算法笔记的主要内容，如果未能解决你的问题，请参考以下文章
树的存储结构的设计及递归遍历(前序,后序,层序)算法实现——Java数据结构与算法笔记
树的存储结构的设计及递归遍历(前序,后序,层序)算法实现——Java数据结构与算法笔记
详解二叉树的遍历问题（前序后序中序层序遍历的递归算法及非递归算法及其详细图示）
数据结构(13)---二叉树之链式结构(前序遍历, 中序遍历, 后序遍历, 层序遍历)